17.2. Доходность портфеля

Ожидаемая доходность портфеля акций (или любых ценных бумаг) есть взвешенная средняя ожидаемой доходности индивидуаных акций, где весами служат доли инвестиций в каждую акцию всей суммы, вложенной в портфель

акций:

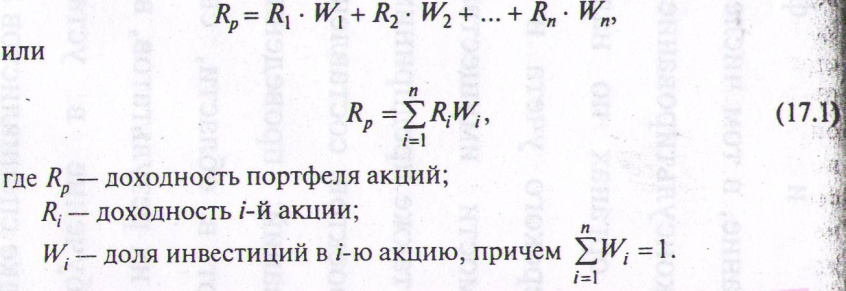
Как следует из приведенной выше формулы, доходность портфель акций будет зависеть от двух параметров: доходности индивидуальной акции и доли инвестиций в каждую акцию.

Предположим, что портфель формируется из двух акций А и В, доходности которых составляют К_А= 10 %, К_в- 20 %.

Доходность портфеля АВ будет зависеть от комбинаций долей инвестиций в каждую акцию (табл. 17.1).

Таблица 17.1

Доли акций А и В и доходность портфеля АВ (К)

Акция		Доля акции в портфеле
А	1,0	0,8	0,6	0,4	0,2	0,0
В	0,0	0,2	0,4	0,6	0,8	1,0
К,%	10	12	14	16	18	20 %

Если портфель составлен только из одной акции А, то ожидаемая доходность составит 10 %. По мере уменьшения доли акции А и увеличения доли акции В, доходность портфеля возрастает. Если все инвестиций вложены в акцию В, то его доходность будет равна 20 %. Ожидаемая доходность портфеля в зависимости от изменения его состава представлена графически на рис. 17.1.

17.3. Риск портфеля

Итак, мы установили, что ожидаемая доходность портфеля акций представляет собой взвешенную среднюю доходность акций, входящих в портфель. Однако задача формирования портфеля акций заключается в том, чтобы учесть не только значения доходности, но и степень риска входящих в портфель акций, которую, как было показано раньше, можно измерить с помощью стандартного отклонения. Продолжим наш пример с акциями. А и В и вычислим стандартное отклонение портфеля из двух этих акций. Для вычисления имеется следующая информация об акциях А и В. Стандартные отклонения этих акций, рассчитанные по итогам предыдущих лет, составляют, со ответственно, 10 % и 60 %. Предположим, что портфель состоит из 40 % акций А И 60 % акций В.

Первое, что можно предположить, это допустить, что стандартное отклонение доходности портфеля есть взвешенная средняя стандартных отклонений для индивидуальных акций: 10-0,4 +60 0,6 = 40%.

Этот результат был бы правильным, если бы цены на акции и соответственно их доходности двигались в совершенно одинаковом на правлении — при росте одной акции точно так же вела бы себя и другая акция. В действительности, как правило, дело обстоит иначе, поэтому риск портфеля не является взвешенной средней стандартно го отклонения индивидуальных акций в портфеле. Для объяснения процедуры вычисления риска портфеля, состоящего из 2 акций, составим следующую таблицу (рис. 17.2).

Дисперсия этого портфеля — это сумма значений величин всех четырех клеток. Чтобы заполнить верхнюю левую клетку нужно взять

произведение дисперсии акции. А и квадрата доли инвестиций в акцию А. Аналогичным образом заполняется нижняя правая клетка значения в этих клетках зависят от величины дисперсии акций

вычисления риска портфеля из двух акций A и B.

Запись в две другие клетки зависит от ковариации акций А и Ковариация может быть выражена как произведение стандартных отклонений двух акций и коэффициента корреляции:

Если в верхней левой и нижней правой клетках мы «взвешивал! дисперсию посредством квадрата долей инвестированных в соответствующие акции (м.>А, м/_в), то в оставшихся двух клетках, когда имеем дело с ковариацией, «весами» является произведение двух долей соответствующих акций

Дисперсия портфеля АВ будет равна сумме слагаемых всех четырех клеток таблицы:

Что касается стандартного отклонения портфеля, то оно есть и что иное, как квадратный корень из дисперсии:

Как следует из приведенных выше формул, стандартное отклонение портфеля зависит от: величин стандартных отклонений, входящих в портфель акций, долей инвестиций в каждую акцию и ковариаций (или коэффициентов корреляции) акций.

Коэффициенты корреляции 2 акций отражают поведение этих акций. Если акции имеют свойство «двигаться» в одном направление (т.е. если цена одной акции идет вверх, то растет курс и другой акции), то коэффициенты корреляции и ковариации позитивны. Если курсы акций двигаются в разных направлениях, то коэффициенты корреляции и ковариации негативны. Если бы движение акции было полностью независимо друг от друга, то коэффициенты корреляции и ковариации были бы равны нулю,

В приведенном выше примере был показан метод расчета стандартного отклонения портфеля, состоящего из 2 акций. Однако этот метод применим для расчета стандартного отклонения любого порт­феля. В таком случае нам необходимо заполнить таблицу с большим числом клеток (рис. 17.3).

Каждая диагональная клетка содержит дисперсию, взвешенную на долю инвестиций в данную акцию, возведенную в квадрат (G²*W²), а каждая из других клеток содержит ковариацию между парой ценных бумаг, взвешенную на произведение долей инвестиций в каждую из акций рассматриваемой пары.

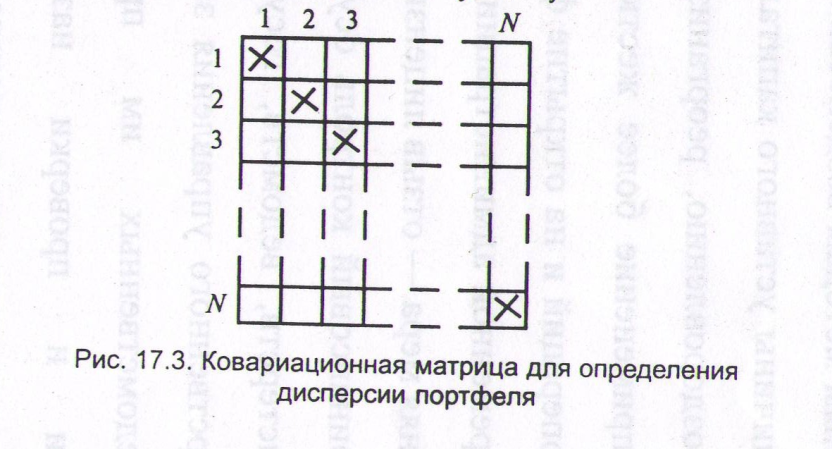
Рис. 17.3. Ковариационная матрица для определения дисперсии портфеля.

Общей формулой для вычисления дисперсии портфеля, состоящего и ценных бумаг, является:

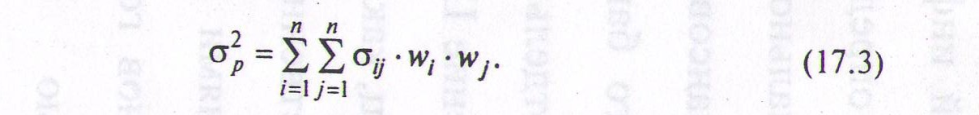
Если портфель состоит из 2 акций, то имеем:

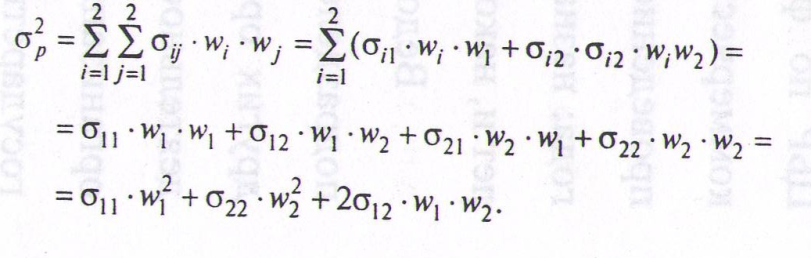
Заметим, что когда i=j, ковариация осесть не что иное, как дисперсия акции i:

Проанализируем, какое влияние на риск портфеля оказывают коэффициенты корреляции входящих в портфель акций. Предположим

что имеются две акции Си D, имеющие строго позитивную корреляцию (Сог=+1).

Значения доходности этих акций за последние 5 лет приведены

табл. 17.2. Составим портфель из этих акций, рассчитаем доходности

и стандартное отклонение портфеля, а также представим эти данные

графически (рис. 17.4).

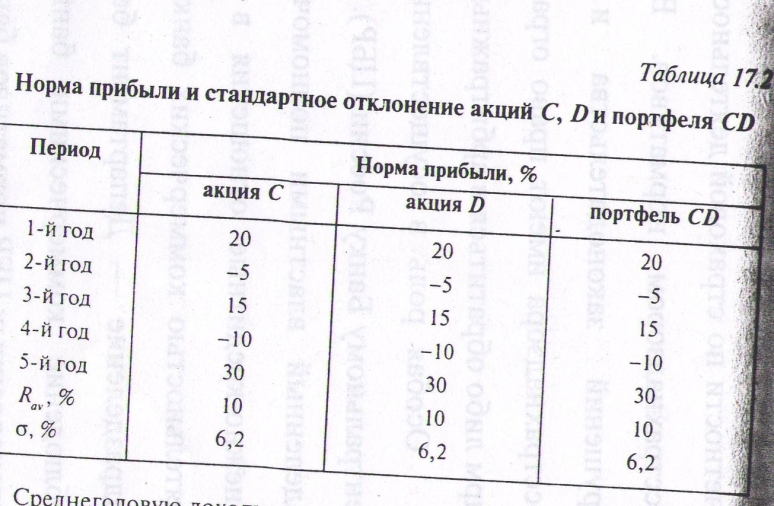
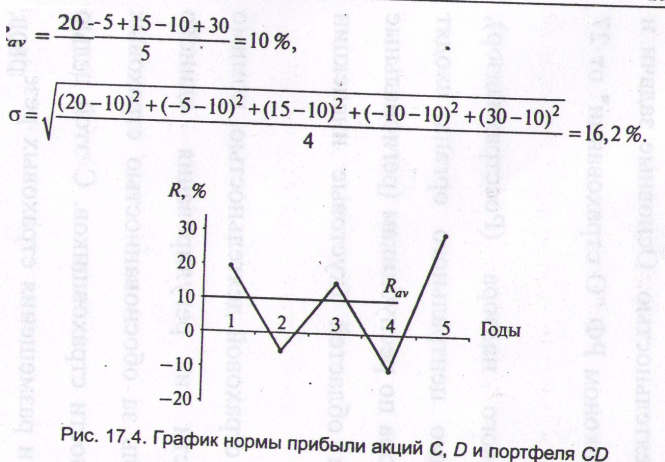
Как показано на рис. 17.4, графики движения значений доходнос­ти акций, имеющих строго позитивную корреляцию, полностью со­впадает с графиком доходности портфеля, составленного из этих ак­ций.

Если допустить, что коэффициент корреляции двух акций равен -1, риск портфеля может быть полностью исключен. Данные об ак­циях портфеля ЕF представлены в табл. 17.3, а графики доход­ности — на рис. 17.5.