Методичка элетротехника 2013

vk.com/club152685050 | vk.com/id446425943

поддерживают постоянным, контролируя его по вольтметру PV1. После этого приступают к настройке цепи, то есть к установке заданных параметров цепи.

Индуктивная катушка помимо индуктивного сопротивления XL обладает еще и активным сопротивлением Rк, которое обусловлено сопротивлением провода катушки и потерями энергии в стальном сердечнике (от гистерезиса и вихревых токов). Поэтому значение активного сопротивления R = Rp + Rк цепи целесообразно установить при резонансе напряжений. Для чего, уменьшая индуктивность L катушки (выдвигая сердечник из нее) и одновременно наблюдая за показаниями фазометра, добиваются совпадения по фазе тока и напряжения в цепи, что соответствует = 0 и соs = 1, и в этом положении сердечник фиксируют в катушке. Затем уменьшают сопротивление реостата до тех пор, пока измеряемые ток I в цепи и активная мощность P не примут расчетных значений, соответствующих резонансу напряжений. При этом возможно незначительное уменьшение cos , который необходимо вновь установить равным единице, изменяя положение сердечника в катушке. После того, как в цепи установлены ток I, мощность Р и коэффициент мощности cos , равные расчетным при резонансе напряжений, и к цепи подведено напряжение U, равное заданному, движок реостата оставляют в этом положении на все время измерений. Очевидно, что при этом в цепи установлено расчетное значение R. Желательно по показаниям приборов проверить cos = P/UI = 1.

Поскольку в цепи установлен резонанс напряжений, что соответствует точке 3 на кривой I = f(L) (рис. 2.2), то измерения начинают именно с точки резонанса напряжений. В табл. 2.3 записывают показания амперметра, ваттметра и фазометра, а также измеренные вольтметром PV2 напряжения UR — на реостате, UК — на катушке и UС — на конденсаторе.

Так как индуктивная катушка обладает и активным сопротивлением, то при резонансе напряжений напряжение Uк на катушке будет

23

vk.com/club152685050 | vk.com/id446425943

на несколько вольт (2...3 В) больше напряжения UC на конденсаторе. Соответственно, напряжение UR на реостате будет меньше расчетного значения, так как активное сопротивление Rp реостата в исследуемой цепи меньше расчетного значения R на величину сопротивления катушки, то есть Rp = R – Rк.

После измерений при резонансе напряжений необходимо провести еще не менее двух-трех измерений при меньших значениях индуктивности и столько же при больших значениях. Сначала полностью выдвигают сердечник из катушки, что соответствует минимальной индуктивности Lmin, и производят все необходимые измерения. Минимальной индуктивности соответствует минимальный ток Imin. Диапазон токов от Imin до Imax при резонансе напряжений разбивают на три примерно равные части и, изменяя индуктивность катушки, устанавливают полученные значения токов и проводят измерения всех величин.

Аналогично поступают при бóльших (L > Lрез) значениях индуктивности, начиная измерения при максимальной индуктивности. Таким образом, получают 7 значений тока и других величин. Данные измерений записывают в табл. 2.3.

Таблица 2.3

Результаты измерений и вычислений

24

vk.com/club152685050 | vk.com/id446425943

Следует иметь в виду, что при изменении положения сердечника в катушке будет изменяться и ее активное сопротивление Rк вследствие изменения магнитных потерь в сердечнике. Поэтому расчетное значение активного сопротивления R цепи, установленное при резонансе напряжений, также будет изменяться в некоторых пределах.

2.2.2. Обработка результатов измерений

На основе опытных данных необходимо вычислить и записать в табл. 2.3 все указанные в ней величины:

– полное сопротивление всей цепи и катушки соответственно:

Z = U / I; Zк = Uк / I;

– активное сопротивление всей цепи, реостата и катушки соответственно:

R = P / I2, RР = UR / I, Rк = R – RР;

–реактивное сопротивление всей цепи X Z 2 R2 , причем перед корнем следует принимать знак плюс (+), если в цепи преобладает индуктивное сопротивление (когда Uк > UС), и знак минус (–), если преобладает емкостное (когда UС > Uк);

–емкостное сопротивление цепи ХС = UС / I;

–индуктивное сопротивление катушки X L 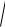Zк2 Rк2 ;

–индуктивность катушки L = XL / ω = XL / 314;

–коэффициент мощности цепи cos = P / UI;

–реактивную и полную мощности цепи Q = UIsin ; S = UI.

По данным табл. 2.3 строят зависимости тока I, напряжений Uк и UС и полного сопротивления Z от индуктивности L (аналогично рис. 2.2). Кроме того, по опытным данным строят три векторные диаграммы напряжений для случаев Lрез, Lmax и Lmin.

25

vk.com/club152685050 | vk.com/id446425943

действующим значениям соответствующих напряжений.

Ha pиc. 2.4 приведена векторная диаграмма напряжений, которую строят по опытным данным следующим образом. Прежде чем приступить к построению векторной диаграммы необходимо

выбрать масштабы тока mI и напряжения mu (например, mU = 20 В/см, что означает, что напряжению 20 В соответству-

элементов за начальный вектор принимают вектор тока I , ко-

торый на рис. 2.4 направлен вертикально вверх. Затем из точки 0 от-

кладывают вектор U R напряжения на реостате, совпадающий по фазе

с вектором тока. Из конца вектораU R под углом /2 в сторону отста-

вания по фазе проводят вектор UC (угол /2 принимают потому, что

0. (Для однозначного определения точки пересечения проводимых дуг следует руководствоваться тем, что активная составляющая напряжения совпадает по фазе с током I ).

26

vk.com/club152685050 | vk.com/id446425943

2.3. ПРОГРАММА РАБОТЫ

Ч. 1. «Расчет и сборка электрической цепи»

1.На основе исходных данных задания рассчитайте все величины, указанные в табл. 2.2, и результаты запишите в ту же таблицу.

2.По данным табл. 2.2 постройте зависимости тока I, напряжений UL, UС и полного сопротивления Z от индуктивности L, как показано на рис. 2.2.

3.Соберите цепь, схема которой показана на рис. 2.3.

Ч.2. «Экспериментальное исследование электрической цепи»

1.Установите в цепи резонанс напряжений при заданном значении емкости С и установите заданное активное сопротивление цепи, как указано в п. 2.2.1.

2.При резонансе напряжений измерьте и запишите в табл. 2.3 все указанные в ней величины.

3.Проведите не менее шести аналогичных измерений в цепи при различных положениях сердечника в катушке, как указано в п. 2.2.1, и результаты запишите в табл. 2.3.

4.По опытным данным вычислите и запишите в табл. 2.3 значения всех указанных в ней величин.

5.По данным табл. 2.3 постройте зависимости тока I, напряжений UL, UС и полного сопротивления Z от индуктивности L, как показано на рис. 2.2.

6.По опытным данным постройте три векторные диаграммы напряжений для случаев: резонанса напряжений, наибольшей и наименьшей индуктивности.

7.Запишите технические данные приборов, использованных в

работе.

8.Проведите анализ полученных результатов, в котором:

– сравните расчетные и опытные данные проверяемого задания;

27

vk.com/club152685050 | vk.com/id446425943

–оцените расхождения между расчетными значениями напряжений на катушке и конденсаторе при резонансе напряжений и значениями, полученными при экспериментальном исследовании цепи, объясните причину этих расхождений;

–оцените расхождения между расчетными и измеренными в опыте значениями напряжений на реостате, объясните причину этих расхождений;

–сравните значения коэффициента мощности cos , полученные по показаниям ваттметра, вольтметра и амперметра, с показаниями фазометра.

2.4.Контрольные вопросы

1.Назовите условие резонанса напряжений.

2.Как определить резонанс напряжений по показаниям измерительных приборов в цепи?

3.Как установить заданные параметры цепи (С и R)?

4.Почему расчетное значение активного сопротивления цепи устанавливают при резонансе напряжений? Как определить значение подводимого к расчетной цепи напряжения U при известных значени-

ях UR, UL и UС?

5.Каково назначение автотрансформатора в работе?

6.Какому крайнему положению сердечника соответствует максимальное индуктивное сопротивление катушки (сердечник полностью в катушке или выдвинут из катушки)?

7.Покажите точки в цепи, к которым следует присоединять вольтметр для измерения напряжений U; UR; UК; UС?

8.Что покажет вольтметр при измерении суммарного напряжения на катушке и конденсаторе при резонансе?

28

vk.com/club152685050 | vk.com/id446425943

РАБОТА 3

ИССЛЕДОВАНИЕ ОДНОФАЗНОЙ ЦЕПИ СИНУСОИДАЛЬНОГО ТОКА ПРИ ПАРАЛЛЕЛЬНОМ СОЕДИНЕНИИ ПРИЕМНИКОВ

Работа состоит из двух частей: ч. 1 «Расчетное и экспериментальное исследование цепи при изменении емкости параллельной ветви» и ч. 2 «Расчетное и экспериментальное исследование цепи при компенсации реактивной мощности».

3.1. РАСЧЕТНОЕ И ЭКСПЕРИМЕНТАЛЬНОЕ ИССЛЕДОВАНИЕ ЦЕПИ ПРИ ИЗМЕНЕНИИ ЕМКОСТИ ПАРАЛЛЕЛЬНОЙ ВЕТВИ

Цель работы — ознакомление с однофазной цепью синусоидального тока, в которую параллельно включены приемники, характеризуемые активным сопротивлением, индуктивностью и емкостью; приобретение практических навыков сборки и исследования электрических цепей. Расчетная часть работы предшествует экспериментальной и выполняется согласно заданию, номер которого из табл. 3.1 указывает преподаватель. Объем работы указан в разделе 3.3 Программа работ.

3.1.1. Указания по расчету

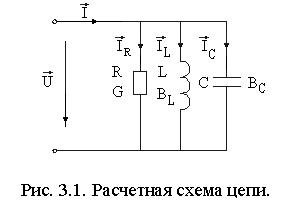
Задача 1. Расчетная схема цепи приведена на рис. 3.1. Исходные данные (напряжение U, активное сопротивление R, индуктивность L и частота f) указаны в табл. 3.1. Необходимо рассчитать величины, приведенные в табл. 3.2, при всех значениях емкости С конденсатора.

При расчете цепи с параллельным соединением приемников удобнее оперировать не сопротивлениями приемников, а их проводимостями. Для простой цепи (рис. 3.1) с параллельным соединением резистора, индуктивного и емкостного элементов, обладающих

29

vk.com/club152685050 | vk.com/id446425943

сопротивлениями R, XL и XC соответственно, их проводимости определяют по соотношениям: активная G = 1 / R, индуктивная BL = 1 / XL = 1 / L, емкостная ВС = 1 / XC = С. При этом, чтобы проводимость выражалась в сименсах (См), индуктивность должна быть выражена в генpи (Гн), а емкость в фарадах (Ф); угловая частота при f = 50 Гц равна = 2πf = 314 рад/c. В задаче 1 проводимости G и BL остаются постоянными, а при изменении емкости будет изменяться проводимость ВС.

30

vk.com/club152685050 | vk.com/id446425943

Окончание табл. 3.1

Другие величины в табл. 3.2 находят следующим образом. Реактивную В и полную Y проводимости цепи определяют по

формулам:

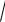B = BL – BС; Y G2 ( BL BС )2 G2 B2 .

Следует иметь в виду, что если BL > BС, то B > 0, а если BL < BС,

то B < 0.

Действующие значения токов в ветвях цепи определяют по закону Ома:

–с активной проводимостью IR = GU = U / R;

–с индуктивной проводимостью IL = BLU = U / L; - емкостной проводимостью IС = BCU = CU;

- в неразветвленной части цепи I = YU.

Сдвиг фаз между напряжением и током в неразветвленной части цепи

arctg BL BC arctg B G G

31

vk.com/club152685050 | vk.com/id446425943

При постоянных значениях G и BL изменение емкости С, или емкостной проводимости ВC, вызывает изменение как значения тока, так и угла . Изменение знака угла означает изменение характера нагрузки. Когда > 0, то нагрузка активно–индуктивная; когда < 0, то нагрузка активно–емкостная.

Коэффициент мощности зависит от параметров цепи следующим образом:

cos = G / Y.

Активную Р и реактивную Q мощности вычисляют по форму-

(BL = BС), то в цепи возникает резонанс токов, т. е. режим, при котором токи IL и IС в ветвях с индуктивной и емкостной проводимостями равны по значению. При этом, если BL = ВС > G, то значения токов IL и IC могут превышать ток I в неразветвленной части цепи в BL / G раз. При резонансе напряжение и ток в неразветвленной части цепи совпадают по фазе ( = 0 и cos = 1), ток I имеет наименьшее возможное значение и равен току в ветви с активной проводимостью I = IR = GU.

32