
- •1) Множества, операции над множествами.
- •Основные числовые множества
- •Операции над множествами
- •Предельные, граничные точки.
- •Открытые и замкнутые множества
- •3) Понятие функции, график функции, способы задания, классификация.
- •Доказательство.
- •5) Бесконечно большие и бесконечно малые последовательности, их свойства.
- •Связь между бесконечно малыми и бесконечно большими последовательностями
- •6) Теорема о пределах числовых последовательностей(предел суммы, произведения, отношения сходящихся последовательностей)
- •8) Теоремы о пределах функций( предел суммы, произведения, отношения, переход и
- •Предел отношения двух функций, имеющих предел в данной точке, равен отношению пределов этих функций в той же точке, если предел знаменателя отличен от нуля:
- •Свойства бесконечно малых и бесконечно больших величин и связь между ними
Свойства бесконечно малых и бесконечно больших величин и связь между ними
Пусть
f1
(x)
и
f
2
(x)
бесконечно малые величины при
,
т.е.
![]() и
и
![]() .
.
1. Сумма (разность) бесконечно малых величин есть величина бесконечно малая:
![]() .
(4.17)
.
(4.17)
2. Произведение бесконечно малых величин есть величина бесконечно малая:
![]() .
(4.18)
.
(4.18)
3.
Произведение бесконечно малой величины
на константу С
или на функцию, имеющую конечный предел
![]() ,
есть величина бесконечно малая:
,
есть величина бесконечно малая:
 .
(4.19)
.
(4.19)
Пусть
![]() и
и
![]() бесконечно
большие величины при
,
т.е.
бесконечно
большие величины при
,
т.е.
![]() и
и
![]() .
.
1. Сумма бесконечно больших величин есть величина бесконечно большая:
![]() .
(4.20)
.
(4.20)
2. Произведение бесконечно больших величин есть величина бесконечно большая:
![]() .
(4.21)
.
(4.21)
3. Произведение бесконечно большой величины на константу С, или на функцию, имеющую конечный предел , есть величина бесконечно большая:
![]() (4.22)
(4.22)
Связь бесконечно малой и бесконечно большой величины
Величина, обратная бесконечно малой величине, есть величина бесконечно большая, и наоборот, величина, обратная бесконечно большой величине, есть величина бесконечно малая.
Пусть
![]() и
и
![]() ,
тогда
,
тогда
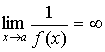 и
и
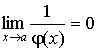 .
.
Символически можно записать:
![]() и
и
![]()
Примеры:
1)
 ;
;
2)
![]() ;
;
3)
![]() .
.
П р и м е ч а н и е. При вычислении пределов возможны следующие комбинации бесконечно малых и бесконечно больших величин, которые называются неопределенностями:
 .
.
11) Непрерывность функций y=f(x). Свойства функций, непрерывных в точке.
12) Непрерывность функций на замкнутом множестве, их свойства
Пусть
![]() есть
пока произвольное множество пространства
есть
пока произвольное множество пространства
![]() ,
и пусть на
определена
функция
,
и пусть на
определена
функция
![]() .
Может случиться, что функция
.
Может случиться, что функция
![]() определена
не на всей окрестности точки
определена
не на всей окрестности точки
![]() (
(![]() - замыкание
),
а только на некоторой ее части. В этом
случае возникает понятие предела функции
в
точке
по
множеству
.
- замыкание
),
а только на некоторой ее части. В этом
случае возникает понятие предела функции
в
точке
по
множеству
.
Число
![]() называется
пределом функции
в
точке
по
множеству
,
если
называется
пределом функции
в
точке
по
множеству
,
если
![]() ,
,
какова
бы ни была последовательность точек
![]() ,
сходящаяся к
,
сходящаяся к
![]() .
.
По
определению, функция
непрерывна
в точке
![]() по
множеству
,
если имеет место равенство
по
множеству
,
если имеет место равенство
![]() ,
(1)
,
(1)
какова
бы ни была последовательность точек
![]() ,
сходящаяся к
.
,
сходящаяся к
.
Приведенное
определение непрерывности можно
сформулировать и на языке
![]() :
функция
непрерывна
в точке
,
если для любого
:
функция
непрерывна
в точке
,
если для любого
![]() найдется
найдется
![]() такое,
что
такое,
что
![]() .
.
Теперь
мы будем предполагать, что
![]() есть
ограниченное замкнутое множество
пространства
есть
ограниченное замкнутое множество
пространства
![]() и
заданная на
функция
и
заданная на
функция
![]() непрерывна
на этом множестве. В этих предположениях
можно доказать следующие замечательные
свойства:
непрерывна
на этом множестве. В этих предположениях
можно доказать следующие замечательные
свойства:
1) Функция ограничена на множестве .
2)
Функция
достигает
на множестве
максимума
и минимума, т. е. существуют в
точки
и
![]() такие,
что
такие,
что
![]() .
.
3) Функция равномерно непрерывна на множестве , т. е. для всякого найдется такое , что
![]()
для
любых
![]() ,
удовлетворяющих неравенствам
,
удовлетворяющих неравенствам
![]() .
.
Как
мы видим, свойства
![]() обобщают
известные уже нам свойства непрерывной
функции
от
одной переменной
обобщают
известные уже нам свойства непрерывной
функции
от
одной переменной
![]() ,
заданной на отрезке
,
заданной на отрезке
![]() .
Подчеркнем, что отрезок
есть
ограниченное замкнутое одномерное
множество. Ведь если какая-либо
последовательность точек (чисел)
.
Подчеркнем, что отрезок
есть
ограниченное замкнутое одномерное
множество. Ведь если какая-либо
последовательность точек (чисел)
![]() ,
принадлежащих к отрезку
,
сходится к некоторой точке (числу)
,
принадлежащих к отрезку
,
сходится к некоторой точке (числу)
![]() ,
то эта точка принадлежит к
,
то эта точка принадлежит к
![]() .
.
Доказательство свойств совершенно аналогично доказательству их для отрезка , приведенному в §§ 3.5 и 3.7. Оно всецело базируется на следующей лемме, обобщающей соответствующую теорему Больцано–Вейерштрасса из § 2.9.
Л
е м м а. Из всякой ограниченной
последовательности точек
![]()
![]() можно
выделить подпоследовательность
можно
выделить подпоследовательность
![]()
![]() ,
сходящуюся к некоторой точке
:
,
сходящуюся к некоторой точке
:
![]() .
.
Д
о к а з а т е л ь с т в о. Так как
последовательность
![]() ограничена,
то существует число
ограничена,
то существует число
![]() такое,
что
такое,
что
![]() .
.
Это
показывает, что координаты точек
![]() также
ограничены. Первая координата образует
ограниченную последовательность
также
ограничены. Первая координата образует
ограниченную последовательность
![]()
![]() ,
и на основании одномерной теоремы
Больцано–Вейерштрасса найдется
подпоследовательность
,
и на основании одномерной теоремы
Больцано–Вейерштрасса найдется
подпоследовательность
![]() натуральных
чисел и некоторое число
натуральных
чисел и некоторое число
![]() такие,
что
такие,
что
![]() .
Вторую координату
.
Вторую координату
![]() рассмотрим
только для найденных натуральных
рассмотрим
только для найденных натуральных
![]() .
Подпоследовательность
.
Подпоследовательность
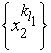 ограничена,
поэтому из нее также можно выбрать
подпоследовательность
ограничена,
поэтому из нее также можно выбрать
подпоследовательность
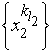 и
число
и
число
![]() такие,
что
такие,
что
![]() .
Так как
.
Так как
![]() есть
подпоследовательность
есть
подпоследовательность
![]() ,
то имеет место одновременно
,
то имеет место одновременно
![]()
![]() .
Продолжая этот процесс, на
.
Продолжая этот процесс, на
![]() -м
его этапе получим подпоследовательность
натуральных чисел
-м
его этапе получим подпоследовательность
натуральных чисел
![]() и
систему чисел
и
систему чисел
![]() такие,
что одновременно
такие,
что одновременно
![]() .
.
Полагая
![]() ,
получим утверждение леммы.
,
получим утверждение леммы.
Д
о к а з а т е л ь с т в о свойства
![]() .
Допустим, что
неограничена
на замкнутом ограниченном множестве
.
Тогда для каждого натурального числа
.
Допустим, что
неограничена
на замкнутом ограниченном множестве
.
Тогда для каждого натурального числа
![]() существует
точка
существует
точка
![]() такая,
что
такая,
что
![]() .
(2)
.
(2)
Так
как множество
ограничено,
то последовательность точек
![]() также
ограничена и, в силу леммы, из нее можно
выделить подпоследовательность
также
ограничена и, в силу леммы, из нее можно
выделить подпоследовательность
![]() ,
сходящуюся к некоторой точке
.
По условию множество
замкнуто,
поэтому точка
,
сходящуюся к некоторой точке
.
По условию множество
замкнуто,
поэтому точка
![]() .
Но в точке
функция
непрерывна
и потому
.
Но в точке
функция
непрерывна
и потому
 .
(3)
.
(3)
Свойство (3) противоречит свойству (2). Поэтому может быть только ограниченной на замкнутом ограниченном множестве .
Д
о к а з а т е л ь с т в о с в о й с т
в а
![]() .
По свойству
непрерывная
на замкнутом ограниченном множестве
функция
ограничена, следовательно, она ограничена
сверху некоторым числом
.
По свойству
непрерывная
на замкнутом ограниченном множестве
функция
ограничена, следовательно, она ограничена
сверху некоторым числом
![]() :
:
![]() .
.
Но тогда существует точная верхняя грань на :
![]() .
(4)
.
(4)
Число
обладает
следующим свойством: Для любого
натурального
найдется
в множестве
точка
![]() такая,
что
такая,
что
![]() .
.
Подпоследовательность , как принадлежащая к ограниченному замкнутому множеству , ограничена:
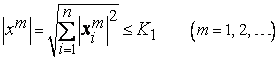 ,
,
и
потому из нее можно выделить
подпоследовательность
![]() ,
сходящуюся к некоторой точке
.
Последнее заключение вытекает из
замкнутости множества
.
,
сходящуюся к некоторой точке
.
Последнее заключение вытекает из
замкнутости множества
.
Но
функция
непрерывна
на множестве
,
следовательно, она непрерывна в точке
![]() ,
поэтому
,
поэтому
 .
.
С другой стороны,
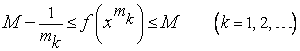 .
.
Переходя
к пределу в этом неравенстве при
![]() ,
получаем
,
получаем
![]() ,
,
т. е.
![]() .
.
Таким образом, верхняя грань (4) достигается в точке , т. е. функция достигает в точке максимума на множестве .
Итак, мы доказали, что существует точка , для которой
![]() .
.
Другая часть свойства о минимуме доказывается аналогично.
Д
о к а з а т е л ь с т в о с в о й
с т в а
![]() .
Допустим, что свойство неверно. Тогда
существует такое
,
что для любого
найдется
пара точек
.
Допустим, что свойство неверно. Тогда
существует такое
,
что для любого
найдется
пара точек
![]() ,
,
![]() ,
удовлетворяющих неравенству
,
удовлетворяющих неравенству
 ,
,
для которых
![]() .
.
Зададим
теперь последовательность положительных
чисел
![]() при
при
![]() .
Для каждого
.
Для каждого
![]() ,
найдутся точки
,
найдутся точки
![]() такие,
что
такие,
что
![]() .
(6)
.
(6)
Так как точки последовательности принадлежат к ограниченному множеству , то эта последовательность ограничена, и из нее, по лемме, можно выделить подпоследовательность , сходящуюся к некоторой точке (в силу замкнутости множества ).
Так
как
![]() при
,
то подпоследовательность
при
,
то подпоследовательность
![]() также
сходится к точке
,
потому что
также
сходится к точке
,
потому что
![]() .
.
По условию функция непрерывна на и, следовательно, непрерывна в точке .
Поэтому
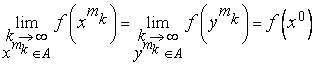 .
.
Теперь, переходя к пределу в (5) при , получаем
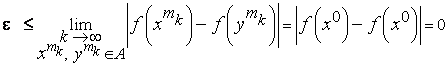
и
мы пришли к противоречию:
![]() .
.
13) Точки разрыва функций y=f(x), их классификация.
