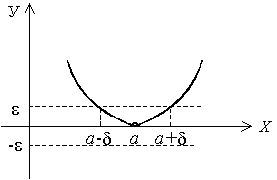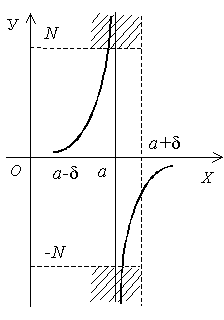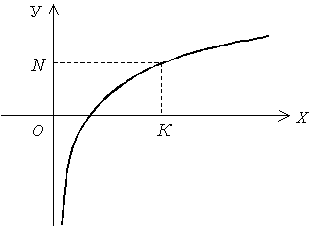8) Теоремы о пределах функций( предел суммы, произведения, отношения, переход и

неравенства в пределах)

 Пусть числовые функции f (x) и g (x) определены на некотором интервале, быть может, кроме точки х₀ этого интервала, и имеют конечные пределы в этой точке

и

Тогда

• если | A | < ∞, то функция f (x) ограничена в окрестности точки х₀.   Доказательство. Так как

то

( ε > 0 ) ( δ = δ (ε) > 0 ) ( 0 < | x - x₀ | < δ ) : | f (x) − A | < ε

Из этого определения следует ограниченность функции: A - ε < f (x) < A + ε в окрестности x₀– δ < x < x₀ + δ, что и требовалось доказать.

Предел алгебраической суммы конечного числа функций, имеющих в данной точке конечный предел, равен алгебраической сумме пределов этих функций в этой же точке:

  Доказательство. Так как по условию теоремы существуют пределы

и

то

( ε > 0 ) ( δ₁ = δ₁ (ε) > 0 ) ( 0 < | x - x₀ | < δ₁ ) : | f (x) − A | < ε ( ε > 0 ) ( δ₂ = δ₂ (ε) > 0 ) ( 0 < | x - x₀ | < δ₂ ) : | g (x) − B | < ε

   Выберем δ = min{δ₁, δ_2}}. В этом случае 0 < | x - x₀| < δ неравенства | f (x) - A| < ε/2 и | g(x) – B | < ε/2 будут выполняться одновременно. И в этом случае модуль разности

0 < | x - x₀| < δ является как угодно малой величиной. Это означает, что выполняется свойство

Что и требовалось доказать.

• Предел произведения конечного числа функций равен произведению пределов этих функций, при условии, что последние существуют.

  Доказательство. Так как по условию теоремы существуют пределы

и

то

( ε > 0 ) ( δ₁ = δ₁ (ε) > 0 ) ( 0 < | x - x₀ | < δ₁ ) : | f (x) – A | < ε, ( ε > 0 ) ( δ₂ = δ₂ (ε) > 0 ) ( 0 < | x - x₀ | < δ₂ ) : | g (x) – B | < ε.

Выберем δ = min{δ₁, δ₂}. В этом случае 0 < | x - x₀| < δ неравенства | f (x) - A | < ε и | g(x) – B | < ε будут выполняться одновременно, и функция g (x) является ограниченной окрестности точки x₀. И в этом случае модуль разности

0 < |x - x₀| < δ является как угодно малой величиной. Это означает, что выполняется свойство

что и требовалось доказать.

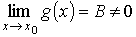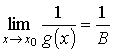• Предел отношения двух функций равен отношению пределов этих функций, при условии, что последние существуют и предел знаменателя не равен нулю.    Докажем вспомогательное утверждение: если , то .    Доказательство. Из условия существования предела

следует

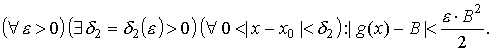
Так как g(x) имеет ненулевой предел, то

В этом случае разность

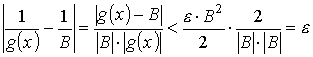
может быть сделана как угодно малой  0 < |x – x₀| < δ если считать, что δ = min{δ₁,δ₂}

• Предел отношения двух функций, имеющих предел в данной точке, равен отношению пределов этих функций в той же точке, если предел знаменателя отличен от нуля:

и ,

то

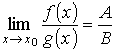
   Доказательство легко вытекает из предыдущих утверждений

• Предел промежуточной функции    Если в некоторой окрестности точки х₀ выполняется неравенство g (x) < f (x) < p (x) и

то

   Доказательство. Так как

то

( ε > 0 ) ( δ₁ = δ₁ (ε) > 0 ) ( 0 < | x - x₀ | < δ₁ ) : | g (x) – A | < ε

Так как

,

то

( ε > 0 ) ( δ₂ = δ₂ (ε) > 0 ) ( 0 < | x - x₀ | < δ₂ ) : | p (x) – A | < ε

Пусть δ = min(δ₁,δ₂} то  0 < |x - x₀| < δ имеем

A – ε < g ( x ) < f ( x ) < p ( x ) < A + ε

то есть

( ε > 0 ) ( δ = δ (ε) > 0 ) ( 0 < | x - x₀ | < δ ) : | f (x) – A | < ε.

Это означает, что

• Предел суперпозиции двух функций.   Пусть функция g отображает выколотую окрестность точки х₀ 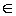(а, b) радиуса δ в выколотую окрестность точки y₀ (c, d). Это значит, что найдётся такое число Δ, что для всех значений аргумента х, не совпадающих с х₀ и меньших по величине этого числа Δ, значения функции не будут принимать значения у₀:

( Δ > 0 ) ( 0 < | x - x₀ | < Δ ) : | g ( x ) – y₀ | > 0.

Пусть функции g: (a, b) → (c, d) и f : (c, d) \ { y₀} → Z и имеют пределы

и

Тогда

   Доказательство. Так как

то

( ε > 0 ) ( σ = σ (ε) > 0 ) ( 0 < | y - y₀ | < σ ) : | f (y) – A | < ε.

Далее  σ > 0, в том числе и для только что указанного, имеем

Это влечёт за собой неравенство | f ( g ( x ) ) - A | < ε, 0 < | x - x₀ | < δ, что и означает

.

• Предельный переход в неравенстве.    Пусть в некоторой выколотой δ – окрестности точки х₀ функции f (x) и g (x) определены и выполнено неравенство f (x) < g (x). Пусть существуют пределы

и

тогда справедливо неравенство А ≤ B.   Доказательство. Пусть это не так,пусть А > B. Выберем как угодно малое положительное число ε таким, чтобы окрестности точек А и В не пересекались

(A – ε; A + ε ) ∩ (B – ε; B + ε ) ) = Ø

Кроме того по предположению

Знак между интервалами означает, что интервал (A - ε; A + ε) лежит правее интервала (B - ε; B + ε).    Из существования пределов функций f (x) и g (x) в точке х₀ следует

( ε > 0 ) ( δ₁ = δ₁ (ε) > 0, δ₁ < Δ) ( 0 < | x - x₀ | < δ₁ ) : | f (x) – A | < ε,

и

( ε > 0 ) ( δ₂ = δ₂ (ε) > 0, δ₂ < Δ) ( 0 < | x - x₀ | < δ₂ ) : | g (x) – B | < ε,

Если принять δ = min {δ₁,δ₂} < δ, то для 0 < | x - x₀| < δ следует неравенство f (x) > g(x). Но это противоречит условию теоремы, значит, наше предположение А > B неверное.

9) Первый и второй замечательные пределы, варианты их записи и применения для описания пределов.

10) Бесконечно малые и бесконечно большие функции, их свойства, сравнения, эквивалентность бесконечно малых.

О п р е д е л е н и е 1. Функция y = f (x) называется бесконечно малой величиной (Б.М.В.) при , если ее предел равен нулю

                                 (4.10)

Геометрически это означает, что функция y = f (x) либо пересекает ось ОХ (рис. 65а), либо касается ее в точке x = a (рис. 65б).

а)	б)
Рис. 65

О п р е д е л е н и е 2. Функция y = f (x)  называется бесконечно малой величиной при , если для каждого положительного сколь угодно малого числа найдется положительное число , такое, что для всех х, удовлетворяющих неравенству , будет выполняться неравенство .

О п р е д е л е н и е 3. Функция  y = f (x) называется бесконечно малой величиной при , если для каждого положительного сколь угодно малого числа найдется сколь угодно большое положительное число такое, что для всех х, удовлетворяющих неравенству будет выполняться неравенство (рис. 66). .      (4.11)

Рис. 66

Геометрически: для всех значений х, которые , значения функции попадают в -окрестность нулевой точки:

Рис. 67

О п р е д е л е н и е 4. Функция y = f (x)   называется бесконечно большой величиной при , если для каждого положительного сколь угодно большого числа N найдется соответствующее сколь угодно малое положительное число y = f (x)  такое, что для всех х, удовлетворяющих неравенству , будет выполняться неравенство : .          (4.12) Геометрически: для всех значений х, попадающих в -окрестность точки а , соответствующие значения функции будут по абсолютной величине больше сколь угодно большого числа N (рис. 67):

                                      (4.13)

О п р е д е л е н и е 5. Функция y = f (x)  называется бесконечно большой величиной при , если для каждого положительного сколь угодно большого числа N найдется соответствующее сколь угодно большое число K(N) такое, что для всех х, удовлетворяющих неравенству , будет выполняться неравенство :

.                                                        (4.14)

Рис. 68

Геометрически: Функция y = f (x) будет бесконечно большой величиной при , если функция может принимать значения по абсолютной величине больше наперед заданного числа N (рис. 68):      (4.15)

В ы в о д ы:

1. Функция  y = f (x) является бесконечно большой величиной, если

   или    .                      (4.16)

2. Данная запись (4.15) является символической.

3. Понятия бесконечно большая величина и бесконечно малая величина относятся только к характеру поведения функции, а не к ее величине вообще.