Предельные, граничные точки.

Граничная точка множества – точка пространства, любая (открытая) окрестность которой содержит как точки, принадлежащие рассматриваемому множеству, так и не принадлежащие ему точки (точки его дополнения). Граничная точка множества может как принадлежать, так и не принадлежать этому множеству.

Пример 1

Для множества точек где n – натуральное число, граничными служат все эти точки и, кроме того, число 0.

Пример 2

Граничными точками интервала (а; b) служат его концы – точки а и b.

Пример 3

Для множества рациональных чисел из отрезка [0; 1] граничными служат вообще все точки этого отрезка – как рациональные, так и иррациональные. 

Пример 4

Для множества точек М(х; у) плоскости, координаты которых удовлетворяют условию  граничными являются точки двух концентрических окружностей с центром в точке О(0; 0) и радиусами r и R. Если в условии заменить строгие неравенства нестрогими, ответ не изменится.

Точка метрического пространства называется предельной точкой множества , если любая её окрестность содержит бесконечно много точек из M. Предельная точка может принадлежать, а может и не принадлежать M. Например, если M — множество рациональных точек отрезка [0;1], то каждая точка этого отрезка является предельной точкой множества M.

Открытые и замкнутые множества

Множество M на прямой называется открытым, если каждая его точка сожержится в этом множестве вместе с некоторым интервалом. Замкнутым называется множество, содержащее все свои предельные точки (т. е. такие, что любой интервал, содержащий эту точку, пересекается со множеством еще хотя бы по одной точке). Например, отрезок является замкнутым множеством, но не является открытым, а интервал, наоборот, является открытым множеством, но не является замкнутым. Бывают множества, которые не являются ни открытыми, ни замкнутыми (например, полуинтервал). Существуют два множества, которые одновременно и замкнутые, и открытые – это пустое и все Z (докажите, что других нет). Легко видеть, что если M открыто, то [M] (или Z \ M – дополнение к множеству M до Z) замкнуто. Действительно, если [M] не замкнуто, то оно не содержит какую-то свою предельную точку m. Но тогда m  M, причем каждый интервал, содержащий m, пересекается с множеством [M], т. е. имеет точку, не лежащую в M, а это противоречит тому, что M – открытое. Аналогично, тоже прямо из определения, доказывается, что если M замкнуто, то [M] открыто (проверьте!).

Теперь докажем следующую важную теорему.

Теорема. Любое открытое множество M можно представить в виде объединения интервалов с рациональными концами (т. е. с концами в рациональных точках).

3) Понятие функции, график функции, способы задания, классификация.

Понятие функции

Функция — математическое понятие, отражающее связь между элементами множеств. Можно сказать, что функция это «закон», по которому каждому элементу одного множества (называемому областью определения) ставится в соответствие некоторый элемент другого множества (называемого областью значений).

Числовая функция — это функция, области определения и значений которой являются подмножествами числовых множеств — как правило, множества вещественных чисел или множества комплексных чисел .

График функции

Графиком функции называется совокупность всех точек на плоскости, прямоугольные координаты которых х и у удовлетворяют уравнению y=f(x). Горизонтальную ось Ох называют осью абсцисс, вертикальную ось Оу - осью ординат. Графическое изображение функции имеет важное значение для её изучения. На графике функции часто непосредственно видны такие её особенности, которые можно было бы установить лишь путём длительных вычислений. Если между величинами х и у существует функциональная связь, то безразлично, какую из этих величин считать аргументом, а какую - функцией.

Существуют разные способы задания функций. 1. Аналитический способ. Аналитический способ - это наиболее часто встречающийся способ задания функции. Заключается он в том, что функция задается формулой, устанавливающей, какие операции нужно произвести над х, чтобы найти у. Например . Рассмотрим первый пример - . Здесь значению x = 1 соответствует , значению x = 3 соответствует и т. д. Функция может быть задана на разных частях множества X разными функциями. Например: Во всех ранее приведенных примерах аналитического способа задания, функция была задана явно. То есть, справа стояла переменная y, а справа формула от переменной х. Однако, при аналитическом способе задания, функция может быть задана и неявно. Например . Здесь, если мы задаем переменной x значение, то, чтобы найти значение переменной у (значение функции), мы должны решить уравнение. Например, для первой заданной функции при х = 3, будем решать уравнение: . То есть, значение функции при х = 3 равно -4/3. При аналитическом способе задания, функция может быть задана параметрически - это, когда х и у выражены через некоторый параметр t. Например, Здесь при t = 2, x = 2, y = 4. То есть, значение функции при х = 2 равно 4. 2. Графический способ. При графическом способе вводится прямоугольная система координат и в этой системе координат изображается множество точек с координатами (x,y). При этом . Пример:

3. Табличный способ. Табличный способ наиболее удобен, когда множество Х конечно. При этом способе составляется таблица, в которой каждому элементу из множества Х, ставится в соответствие число Y. Пример:

4) Последовательность в R. Определение предела. Критерий Коши о сходимости числовой последовательности.

Числовые последовательности

Последовательностью называется множество чисел, перенумерованных с помощью натуральных чисел и расставленных в порядке возрастания их номеров x₁,x₂,...x_n Числа x₁,x₂,...,x_n — называются элементами последовательности, символ x_n — общим элементом, а число n — его номером. Сокращенно последовательность обозначается символом {x_n}.

Предел последовательности

Окрестностью точки x₀ называется любой интервал, содержащий эту точку.

δ — окрестностью точки x₀ U_δ (x₀) называется интервал длиной 2δ с центром в этой точке.

Определение предела последовательности

Число а называется пределом последовательности {x_n}, если для любого ε > 0 найдется номер n₀ = n₀(ε) ∈ N такой, что для всех номеров n > n₀ выполняется неравенство |x_n — a| <ε

Число b называется пределом последовательности {x_n}=x₁, x₂,..., x_n (lim {x_n} = b; n→∞)

Последовательность {x_n}, имеющая конечный предел а, называется сходящейся. Последовательность, имеющая бесконечный предел или вообще не имеющая предела, называется расходящейся

Свойства сходящихся последовательностей

Теорема 1.

Сходящаяся последовательность имеет только один предел.

Теормера О сходимости подпоследовательности

Теорема Об арифметических действиях над сходящимися последовательностями

Теорема 8 Критерий Коши сходимости последовательности

Для того чтобы последовательность {x_n} сходилась, необходимо и достаточно, чтобы ∀ε >0 ∃номер n₀ такой, что ∀n > n₀ и любого p∈N выполнялось неравенство |x_n+p - x_n| <ε

Если предел последовательности равен нулю, то ее называют бесконечно малой

Теорема Вейерштрасса. Всякая монотонная и ограниченная последовательность имеет предел

Последовательность называется возрастающей, если для любого выполняется неравенство

xn + 1 > xn.

Последовательность называется убывающей, если для любого выполняется неравенство

xn + 1 < xn.

Если в этих определениях неравенство будет нестрогим, то последовательности будут называться соответственно неубывающей и невозрастающей.

Возрастающие и убывающие последовательности называют строго монотонными. Неубывающие и невозрастающие последовательности называют монотонными.

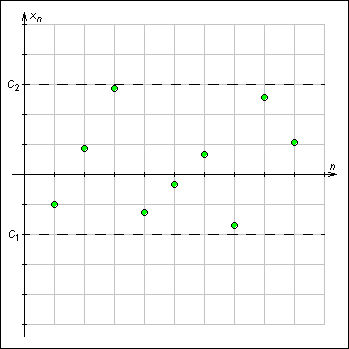
Последовательность {x_n} называется ограниченной снизу (сверху), если существует такое число C, что все члены последовательности удовлетворяют условию x_n ≥ C (x_n ≤ C). Последовательность, ограниченную как сверху, так и снизу, называют ограниченной.

Рисунок 1.1.2.1. Последовательность называют ограниченной, если C1 ≤ xn ≤ C2.

Геометрически ограниченность последовательности означает, что все ее значения лежат на некотором отрезке.

Можно показать, что если последовательность имеет предел, то она ограничена.

Заметим, что не всякая ограниченная последовательность является сходящейся. Примером расходящейся ограниченной последовательности может служить последовательность {x_n}: x_n = (–1)ⁿ.

Теорема ( Критерий Коши ). Для того, чтобы последовательность {x_n} сходилась, необходимо и достаточно чтобы она была фундаментальной.