
- •1) Множества, операции над множествами.
- •Основные числовые множества
- •Операции над множествами
- •Предельные, граничные точки.
- •Открытые и замкнутые множества
- •3) Понятие функции, график функции, способы задания, классификация.
- •Доказательство.
- •5) Бесконечно большие и бесконечно малые последовательности, их свойства.
- •Связь между бесконечно малыми и бесконечно большими последовательностями
- •6) Теорема о пределах числовых последовательностей(предел суммы, произведения, отношения сходящихся последовательностей)
- •8) Теоремы о пределах функций( предел суммы, произведения, отношения, переход и
- •Предел отношения двух функций, имеющих предел в данной точке, равен отношению пределов этих функций в той же точке, если предел знаменателя отличен от нуля:
- •Свойства бесконечно малых и бесконечно больших величин и связь между ними
1) Множества, операции над множествами.
Множеством называется совокупность некоторых элементов, объединенных каким-либо общим признаком. Элементами множества могут быть числа, фигуры, предметы, понятия и т.п.
Множества обозначаются прописными буквами, а элементы множество строчными буквами. Элементы множеств заключаются в фигурные скобки.
Если элемент x принадлежит множеству X, то записывают x ∈ Х (∈ — принадлежит). Если множество А является частью множества В, то записывают А ⊂ В (⊂ — содержится).
Множество может быть задано одним из двух способов: перечислением и с помощью определяющего свойства.
Например, перечислением заданы следующие множества:
А={1,2,3,5,7} — множество чисел
Х={x1,x2,...,xn} — множество некоторых элементов x1,x2,...,xn
N={1,2,...,n} — множество натуральных чисел
Z={0,±1,±2,...,±n} — множество целых чисел
Множество (-∞;+∞) называется числовой прямой, а любое число — точкой этой прямой. Пусть a — произвольная точка числовой прямой иδ — положительное число. Интервал (a-δ; a+δ) называется δ-окрестностью точки а.
Множество Х ограничено сверху (снизу), если существует такое число c, что для любого x ∈ X выполняется неравенство x≤с (x≥c). Число с в этом случае называется верхней(нижней) гранью множества Х. Множество, ограниченное и сверху и снизу, называется ограниченным. Наименьшая (наибольшая) из верхних (нижних) граней множества называется точной верхней (нижней) гранью этого множества.
Основные числовые множества
N |
{1,2,3,...,n} Множество всех натуральных чисел |
Z |
{0, ±1, ±2, ±3,...} Множество целых чисел. Множество целых чисел включает в себя множество натуральных. |
Q |
Множество рациональных чисел. Кроме
целых чисел имеются ещё и дроби. Дробь
— это выражение вида
Таким образом любое рациональное число можно записать десятичной дробью — конечно или бесконечной периодической.
|
R |
Множество всех вещественных чисел. Иррациональные числа — это бесконечные непериодические дроби. К ним относятся:
Вместе два множества (рациональных и иррациональных чисел) — образуют множество действительных (или вещественных) чисел.
|
Операции над множествами
Два множества А и В равны (А=В), если они состоят из одних и тех же элементов. Например, если А={1,2,3,4}, B={3,1,4,2} то А=В.
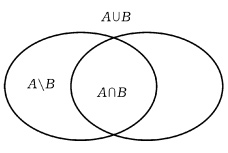
Объединением (суммой) множеств А и В называется множество А ∪ В, элементы которого принадлежат хотя бы одному из этих множеств. Например, если А={1,2,4}, B={3,4,5,6}, то А ∪ B = {1,2,3,4,5,6}
Пересечением (произведением) множеств А и В называется множество А ∩ В, элементы которого принадлежат как множеству А, так и множеству В. Например, если А={1,2,4}, B={3,4,5,2}, то А ∩ В = {2,4}
Разностью множеств А и В называется множество АВ, элементы которого принадлежат множесву А, но не принадлежат множеству В. Например, если А={1,2,3,4}, B={3,4,5}, то АВ = {1,2}
Симметричной разностью множеств А и В называется множество А Δ В, являющееся объединением разностей множеств АВ и ВА, то есть А Δ В = (АВ) ∪ (ВА). Например, если А={1,2,3,4}, B={3,4,5,6}, то А Δ В = {1,2} ∪ {5,6} = {1,2,5,6}
2) Пространство R, метрика, окрестность точки. Предельные, граничные точки. Открытые и замкнутые множества в R.
Определение 1. Множество R называется метрическим пространством, если каждой паре его элементов х и у ( х є R, у є R) поставлено в соответствие неотрицательное вещественное число ρ(x,y) , удовлетворяющие следующим условиям:
ρ(x,y)=0 тогда и только тогда, когда х=у (аксиома тождества);
ρ(x,y)= ρ(x,y) (аксиома симметрии);
ρ(x,y)+ρ(x,z) ≥ ρ(x,z) (аксиома треугольника).
Число ρ(x,y) называется расстоянием между элементами х и у, перечисленные три условия – аксиомами метрики. Очевидно, что аксиомы метрики представляют собой формулировку наиболее общих свойств расстояния между точками трехмерного евклидового пространства.
Замечание 1. Очевидно, имея одно множество и метризуя его различными способами (определяя расстояние между элементами множества по-разному), получаем различные метрические пространства.
Замечание
2.
Всякое
подмножество
R1
метрического пространства R
(R1
![]() R)
в свою очередь является метрическим
пространством с той же метрикой, что и
в R
R)
в свою очередь является метрическим
пространством с той же метрикой, что и
в R
Определение 2. Последовательность элементов (точек) х1, х2,…хn,... метрического пространства R имеет своим пределом элемент (точку) х є R, пишут:
![]()
Если
числовая последовательность
![]() сходится
к нулю, т.е
сходится
к нулю, т.е
![]() .
.
ОКРЕСТНОСТЬ точки в метрическом пространстве, множество всех точек, расстояние которых до данной точки меньше некоторого положительного числа. Это - т.н. сферическая окрестность. В более общем случае под окрестностью понимают любое открытое множество, содержащее данную точку.
