11. Ошибка выборки (доверительный интервал)

Отклонение результатов, полученных с помощью выборочного наблюдения от истинных данных генеральной совокупности.

Ошибка выборки бывает двух видов – статистическая и систематическая. Статистическая ошибка зависит от размера выборки. Чем больше размер выборки, тем она ниже.

Систематическая ошибка зависит от различных факторов, оказывающих постоянное воздействие на исследование и смещающих результаты исследования в определенную сторону.

Пример:

- Использование любых вероятностных выборок занижает долю людей с высоким доходом, ведущих активный образ жизни. Происходит это в силу того, что таких людей гораздо сложней застать в каком-либо определенном месте (например, дома).

- Проблема респондентов, отказывающихся отвечать на вопросы анкеты (доля «отказников» в Москве, для разных опросов, колеблется от 50% до 80%)

В некоторых случаях, когда известны истинные распределения, систематическую ошибку можно нивелировать введением квот или перевзвешиванием данных, но в большинстве реальных исследований даже оценить ее бывает достаточно проблематично.

Измерить можно лишь случайные ошибки, т. е. ошибки, обус­ловленные неполнотой изучения реально существующей сово­купности.

Определение численности выборки

Формулы для определения численности выборки n не сложно получить непосредственно из формул ошибок выборки.

Из формулы предельной ошибки выборки для повторного отбора получают необходимую численность выборки, предварительно возведя в квадрат обе части равенства:

1. Для средней количественного признака:

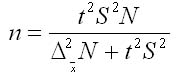
2. Для доли (альтернативного признака):

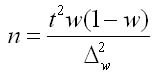
Аналогично из формулы предельной ошибки выборки для бесповторного отбора определяем:

1. Для средней количественного признака:

2. Для доли (альтернативного признака):

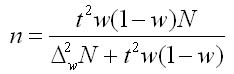
Эти формулы показывают, что с увеличением предполагаемой ошибки выборки необходимый объем выборки уменьшается значительно.

На основании теоремы Чебышева П. Л. величина средней ошибки при случайном повторном отборе в контрольных работах по статистике рассчитывается по формуле (для среднего количественного признака):

где числитель — дисперсия признака х в выборочной совокупности;

n — численность выборочной совокупности.

Для альтернативного признака формула средней ошибки выборки для доли по теореме Я. Бернулли рассчитывается по формуле:

где р(1- р) — дисперсия доли признака в генеральной совокупности;

n — объем выборки.

Вследствие, того что дисперсия признака в генеральной совокупности точно не известна, на практике используют значение дисперсии, которое рассчитано для выборочной совокупности на основании закона больших чисел. Согласно данному закону выборочная совокупность при большом объеме выборки достаточно точно воспроизводит характеристики генеральной совокупности.

Поэтому расчетные формулы средней ошибки при случайном повторном отборе будут выглядеть таким образом:

1. Для среднего количественного признака:

где S^2 — дисперсия признака х в выборочной совокупности;

n — объем выборки.

2. Для доли (альтернативного признака):

где w (1 - w) — дисперсия доли изучаемого признака в выборочной совокупности.

В теории вероятностей было показано, что генеральная дисперсия выражается через выборочную согласно формуле:

В случаях малой выборки, когда её объем меньше 30, необходимо учитывать коэффициент n/(n-1). Тогда среднюю ошибку малой выборки рассчитывают по формуле:

Так как в процессе бесповторной выборки сокращается численность единиц генеральной совокупности, то в представленных выше формулах расчета средних ошибок выборки нужно подкоренное выражение умножить на 1- (n/N).

Расчетные формулы для такого вида выборки будут выглядеть так:

1. Для средней количественного признака:

где N — объем генеральной совокупности; n — объем выборки.

2. Для доли (альтернативного признака):

где 1- (n/N) - доля единиц генеральной совокупности, не попавших в выборку.

Поскольку n всегда меньше N, то дополнительный множитель 1 - (n/N) всегда будет меньше единицы. Это означает, что средняя ошибка при бесповторном отборе всегда будет меньше, чем при повторном. Когда доля единиц генеральной совокупности, которые не попали в выборку, существенная, то величина 1 - (n/N) близка к единице и тогда расчет средней ошибки производится по общей формуле.

Средняя ошибка зависит от следующих факторов:

1. При выполнении принципа случайного отбора средняя ошибка выборки определяется во-первых объемом выборки: чем больше численность, тем меньше величины средней ошибки выборки. Генеральная совокупность характеризуется точнее тогда, когда больше единиц данной совокупности охватывает выборочное наблюдение

2. Средняя ошибка также зависит от степени варьирования признака. Степень варьирования характеризуется дисперсией. Чем меньше вариация признака (дисперсия), тем меньше средняя ошибка выборки. При нулевой дисперсии (признак не варьируется) средняя ошибка выборки равна нулю, таким образом, любая единица генеральной совокупности будет характеризовать всю совокупность по этому признаку.

12. Зависимость Статистическая

такая связь двух случайных величин, при которой распределение вероятностей одной из них зависит от того, какие возможные значения приняла другая величина.

Корреля́ция (корреляционная зависимость) — статистическая взаимосвязь двух или нескольких случайных величин (либо величин, которые можно с некоторой допустимой степенью точности считать таковыми). При этом изменения значений одной или нескольких из этих величин сопутствуют систематическому изменению значений другой или других величин

Функциональной зависимостью называют зависимость, где каждому значению переменной Х соответствует единственное значение У.

13. Эмпирическая регрессия строится по данным аналитической или комбинационной группировок и представляет собой зависимость групповых средних значений признака-результата от групповых средних значений признака-фактора. Графическим представлением эмпирической регрессии – ломаная линия, составленная из точек, абсциссами которых являются групповые средние значения признака-фактора, а ординатами – групповые средние значения признака-результата. Число точек равно числу групп в группировке.

Корреляционное поле – точечный график в системе координат. Рекомендуется наносить эмпирическую линию регрессии на корреляционное поле.

Эмпирическая линия регрессии отражает основную тенденцию рассматриваемой зависимости. Если эмпирическая линия регрессии по своему виду приближается к прямой линии, то можно предположить наличие прямолинейной корреляционной связи между признаками. А если линия связи приближается к кривой, то это может быть связано с наличием криволинейной корреляционной связи

14) Регрессио́нный (линейный) анализ — статистический метод исследования зависимости между зависимой переменной Y и одной или несколькими независимыми переменными X1,X2,...,Xp. Независимые переменные иначе называют регрессорами или предикторами, а зависимые переменные — критериальными. Терминология зависимых и независимых переменных отражает лишь математическую зависимость переменных (см. Ложная корреляция), а не причинно-следственные отношения.

Цели регрессионного анализа

Определение степени детерминированности вариации критериальной (зависимой) переменной предикторами (независимыми переменными)

Предсказание значения зависимой переменной с помощью независимой(-ых)

Определение вклада отдельных независимых переменных в вариацию зависимой

Регрессионный анализ нельзя использовать для определения наличия связи между переменными, поскольку наличие такой связи и есть предпосылка для применения анализа.

15) ЛИНЕЙНАЯ РЕГРЕССИЯ - Статистический метод измерения степени, в которой изменения одной переменной ассоциируются с изменениями других. Предполагается, что отношение между одной переменной – "левой руки", или зависимой переменной, и другими – "правой руки", или независимыми переменными, можно выразить в виде следующей линейной функции: yi = α0+α1x1i+α2x2i+...+αNxNi+εi где εi является стохастическим поправочным членом. Целью является выбор оценочных значений α0, α1, и т.д., которые минимизируют сумму Σiεi2=Σiyi–(α0+α1x1i+α2x2i+...+αNxNi)2 Это неявная переменная в y. Хотя различные х считаются независимыми переменными, а у – зависимой переменной, регрессия является лишь измерением соответствия и не подразумевает, что существует какое-либо каузальное отношение, и если оно вообще есть, то говорит только об одном: у зависит от х.

Основная цель построения регрессии - это стремление, используя некий

набор «наблюдений», получить количественные и качественные зависимости для

различных соотношений. Очевидно, что мы не можем просчитать влияние

абсолютно всех факторов - мы осознанно упрощаем действительность, строя

модель. Таким образом, мы работаем уже с некоторой эконометрической моделью,

которая выражается в достаточно простой математической форме. Отличительной

особенностью эконометрической модели будет являться наличие случайной

(стохастической) составляющей (ei), учитывающей возможные ошибки при сборе

данных, построении выборки и ее обработки.

Простейшей эконометрической моделью является простая линейная

регрессия, имеющая вид:

Yj = а + bXi + ei,

где

Yj- является зависимой переменной;

Xi - регрессором (объясняющей переменной);

а и b – коэффициенты;

еi - случайная составляющая.

16)

При изучении корреляционной связи важным направлением анализа является оценка степени тесноты связи.

Понятие степени тесноты связи между двумя признаками возникает вследствие того, что в реальной действительности на изменение результативного признака влияют несколько факторов. При этом влияние одного из факторов может выражаться более заметно и четко, чем влияние других факторов. С изменением условий в качестве главного, решающего фактора может выступать другой.

При статистическом изучении взаимосвязей, как правило, учитываются только основные факторы. А вопрос необходимо ли вообще изучать более подробно данную связь и практически ее использовать, решается с учетом степени тесноты связи.

Зная количественную оценку тесноты корреляционной связи, таким образом, можно решить следующую группу вопросов:

1. необходимо ли глубокое изучение данной связи между признаками и целесообразно ли ее практическое применение;

2. сопоставляя оценки тесноты связи для различных условий, можно судить о степени различий в ее проявлении в конкретных условиях;

3. последовательное рассмотрение и сравнение признака у с различными факторами (х1, х21, …) позволяет выявить, какие из этих факторов в данных конкретных условиях являются главными, решающими факторами, а какие второстепенными, незначительными факторами;

Показатели тесноты связи должны удовлетворять ряду основных требований:

1. величина показателя степени тесноты связи должна быть равна или близка к нулю, если связь между изучаемыми признаками (процессами, явлениями) отсутствует;

2. при наличии между изучаемыми признаками (х и у) функциональной связи величина степень тесноты связи равна единице;

3. при наличии между признаками (х и у) корреляционной связи показатель тесноты связи выражается правильной дробью, которая по величине тем больше, чем теснее связь между изучаемыми признаками (стремится к единице);

4. при прямолинейной корреляционной связи показатели тесноты связи отражают и направление связи: знак (+) означает наличие прямой (положительной) связи; а знак (-) – обратной (отрицательной).

Для характеристики степени тесноты корреляционной связи могут применяться различные статистические показатели: коэффициент Фехнера (КФ), коэффициент линейной (парной) корреляции (r’), коэффициент детерминации, корреляционное отношение ( ), индекс корреляции, коэффициент множественной корреляции (R), коэффициент частной корреляции (r’) и др.

В данном вопросе рассмотрим коэффициент линейной корреляции (r) и корреляционное отношение ( ).

Более совершенным статистических показателем степени тесноты корреляционной связи является линейный коэффициент корреляции (r), предложенный в конце XIX в.

17) Корреляционная связь (которую также называют неполной, или статистической) проявляется в среднем, для массовых наблюдений, когда заданным значениям зависимой переменной соответствует некоторый ряд вероятных значений независимой переменной. Объяснение тому – сложность взаимосвязей между анализируемыми факторами, на взаимодействие которых влияют неучтенные случайные величины. Поэтому связь между признаками проявляется лишь в среднем, в массе случаев. При корреляционной связи каждому значению аргумента соответствуют случайно распределенные в некотором интервале значения функции. Если изучаются более чем две переменные – связь называют множественной.

Парная, или однофакторная, корреляция — это неполная пря­мая или обратная связь между одним признаком-следствием и одним признаком-фактором. Она позволяет относительно аде­кватно измерить выявленную связь, чего не дают другие методы статистического анализа. Ценность корреляционного анализа сле­дует оценивать, исходя из известного постулата: наука начина­ется с измерения.

ч Корреляционное измерение связи, как правило, производится после установления ее наличия и характера (прямая, обратная) в процессе других видов статистического анализа: сводки и груп­пировки данных, расчета относительных и средних величин, со­ставления вариационных, динамических и особенно параллель­ных рядов.

Корреляционная матрица – матрица, элементами которой являются парные коэффициенты корреляции рассматриваемых случайных величин. Понятно, что такая матрица симметрична, а на ее диагонали находятся единицы. Корреляционная матрица является исходным объектом для алгоритмов расчета практически всех методов многомерного статистического анализа