
- •Формування математичних виразів, формул і тексту: способи, можливості, приклади.
- •Розв’язок систем нелінійних рівнянь: способи організації, пояснення приклади.
- •Логічні оператори: призначення, способи створення і застосування, приклади
- •Закони розподілу випадкових величин
- •Диференціювання та похідні вищих порядків
- •Розв’язок систем лінійних алгебраїчних рівнянь
- •Im(z) - уявна частина комплексного числа z;
- •Оператор інтегрування: застосування, пояснення, приклади.
- •Диференціювання, похідні вищих порядків: застосування, пояснення, приклади.
- •Похідні вищих порядків
Логічні оператори: призначення, способи створення і застосування, приклади
Результатом дії логічних, або булевих, операторів являються тільки числа 0 (якщо логічний вираз відповідає істині) або 1 (якщо логічний вираз відповідає хибному результату). Логічні оператори вставляються з панелі Boolean (Булеві оператори). На ній розміщені оператори порівняння (відношення) та булеві оператори (Мал. 2.1).
Перерахуємо логічні
оператори:
- більше (Greater
Than) (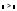 );
-
менше (Less
Than) (
);
-
менше (Less
Than) (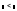 );
-
більше або рівно (Greater
Than or Equal) (
);
-
більше або рівно (Greater
Than or Equal) (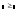 ),
(Ctrl + 0);
-
менше або рівно (Less
Than or Equal) (
),
(Ctrl + 0);
-
менше або рівно (Less
Than or Equal) (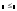 ),
(Ctrl
+ 9);
- рівно
(Equal)
(
),
(Ctrl
+ 9);
- рівно
(Equal)
( ),
(Ctrl + =);
-
не рівно (Not
Equal to) (
),
(Ctrl + =);
-
не рівно (Not
Equal to) (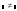 ),
(Ctrl + 3);
- і
(And) (
),
(Ctrl + 3);
- і
(And) (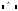 ),
(Ctrl +Shift + 7);
-
або (Or) (
),
(Ctrl +Shift + 7);
-
або (Or) (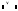 ),
(Ctrl +Shift + 6);
-
виключення або (Exclusive
or) (
),
(Ctrl +Shift + 6);
-
виключення або (Exclusive
or) ( ),
(Ctrl +Shift + 5);
-
заперечення (Not)
(
),
(Ctrl +Shift + 5);
-
заперечення (Not)
(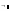 ),
(Ctrl +Shift + 1).
),
(Ctrl +Shift + 1).
Застосування операторів порівняння та булевих операторів приведено в прикладах 2.13 та 2.14.
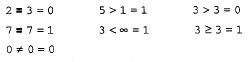
Арифметичні оператори: призначення, способи створення і застосування, прикади.
Обчислювальні оператори
Обчислювальні оператори вставляються в документи за допомогою панелі інструментів Calculus (Обчислення). При натисканні кожної з кнопок у документі з'являється символ відповідної математичної дії, позначений декількома покажчиками. Перелічимо основні обчислювальні оператори:
-
похідна
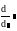 (приклад 2.8)
(приклад 2.8)
-
N-я похідна
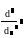 (приклад 2.8);
(приклад 2.8);
-
визначений інтеграл (приклад 2.9)
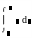 ;
;
-
невизначений інтеграл
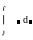 (приклад 2.9).
(приклад 2.9).
-
сума
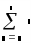 (приклад 2.10);
(приклад 2.10);
-
добуток
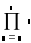 (приклад 2.10);
(приклад 2.10);
-
сума ранжованої змінної
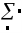 (приклад 2.11);
(приклад 2.11);
-
добуток ранжованої змінної
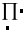 (приклад 2.11).
(приклад 2.11).
-
межа двостороння
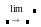 (приклад 2.12);
(приклад 2.12);
-
межа ліва
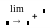 (приклад 2.12);
(приклад 2.12);
-
межа права
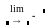 (приклад 2.12);
(приклад 2.12);
Приведемо найпростіші приклади застосування обчислювальних операторів:

Приклад 2.8. Оператори обчислення похідних

Приклад 2.9. Оператори інтегрування
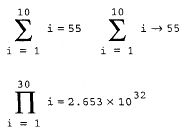
Приклад 2.10. Оператори підсумовування й обчислення добутку
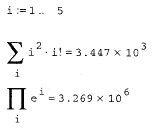
Приклад 2.11. Оператори підсумовування і добутку ранжованої змінної
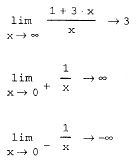
Закони розподілу випадкових величин
Рівномірний закон розподілу Показниковий закон розподілу Нормальний закон розподілу
Нормальний розподіл (розподіл Ґауса) — розподіл ймовірностей випадкової величини, що характеризується густиною ймовірності
![]()
де μ — математичне сподівання, σ2 — дисперсія випадкової величини.
Центральна гранична теорема стверджує, що нормальний розподіл виникає тоді, коли дана випадкова величина являє собою суму великого числа незалежних випадкових величин, кожна з яких грає в утворенні всієї суми незначну роль. Наприклад, відстань від влучення снаряду гармати до цілі при великій кількості пострілів характеризується саме нормальним розподілом.
Нормально розподілена випадкова величина позначається так: ξ ~ N(μ,σ2).
Диференціювання та похідні вищих порядків
За допомогою Mathcad можна обчислювати похідні скалярних функцій будь-якої кількості аргументів а також похідні вищих порядків від 0-го до 5-го порядку включно. І функції, і аргументи можуть бути як дійсними, так і комплексними числами.
Чисельне та символьне диференціювання функції f(x)=cos(x)*ln(x) наведено в прикладі. Потрібно не забути попередньо визначати точку, у якій відбувається чисельне диференціювання.
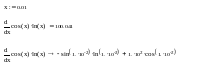
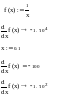
Щоб обчислити похідну функції f (х) N-го порядку в точці х, потрібно проробити ті ж самі дії, що і при взятті першої похідної , за тим виключенням, що замість оператора похідної необхідно застосувати оператор похідної N-го порядку (Nth Derivative)
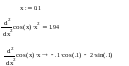
Оператори обчислення сум та добутків з чотирма покажчиками зручні у випадку невеликої кількості доданків. В іншому випадку використовуються оператори з індексними змінними. В першому випадку вказується нижня і верхня межа діапазона зміни індексної змінної. Крок дискретності змінної при цьому дорівнює одиниці (приклад 6.8). У випадку обчислення суми чи добутку індексної змінної, крок зміни якої відмінний від нуля, доцільно використовувати інший вид операторів, в яких змінна вказується без меж діапазону її зміни
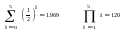
Обчислення за цілочисельними значеннями
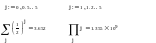
Обчислення за індексними змінними
