1. Для каждой из подсистем назначаются частные показатели эффективности

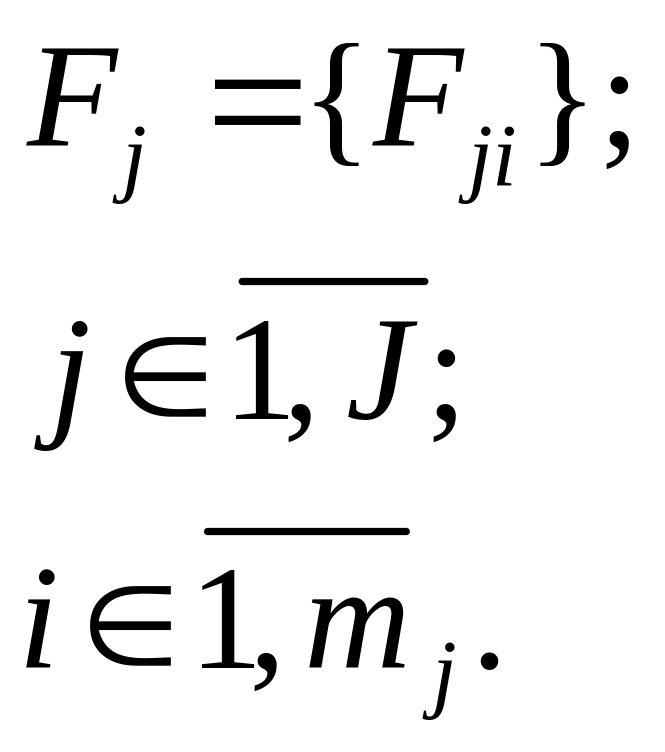
В качестве этих показателей могут быть непосредственно сами ТТХ подсистем , либо свертки ТТХ .

Если используются свертки, то индекс меняется

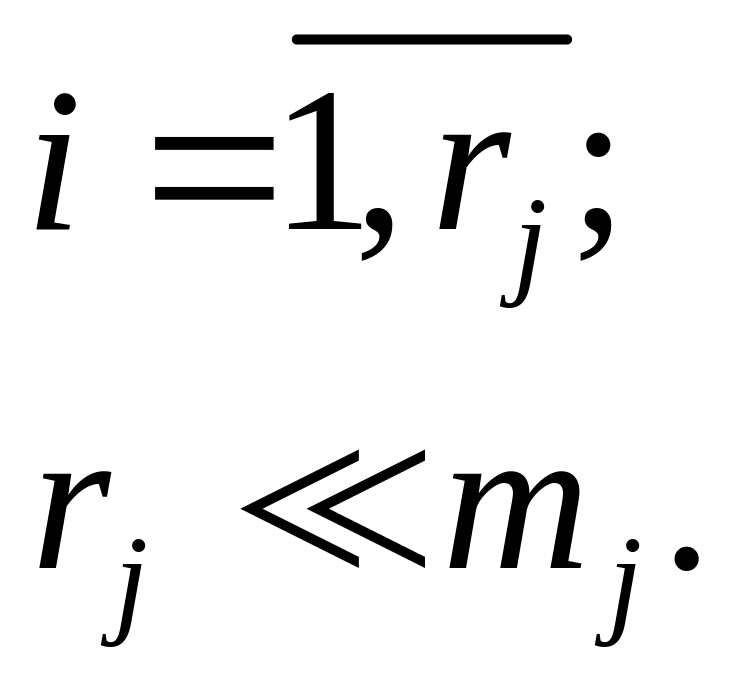
Далее составляется ЦФ:

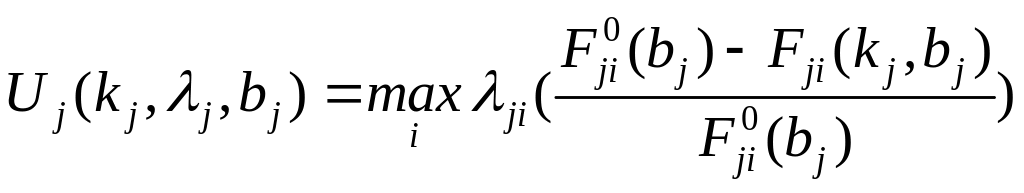(2)

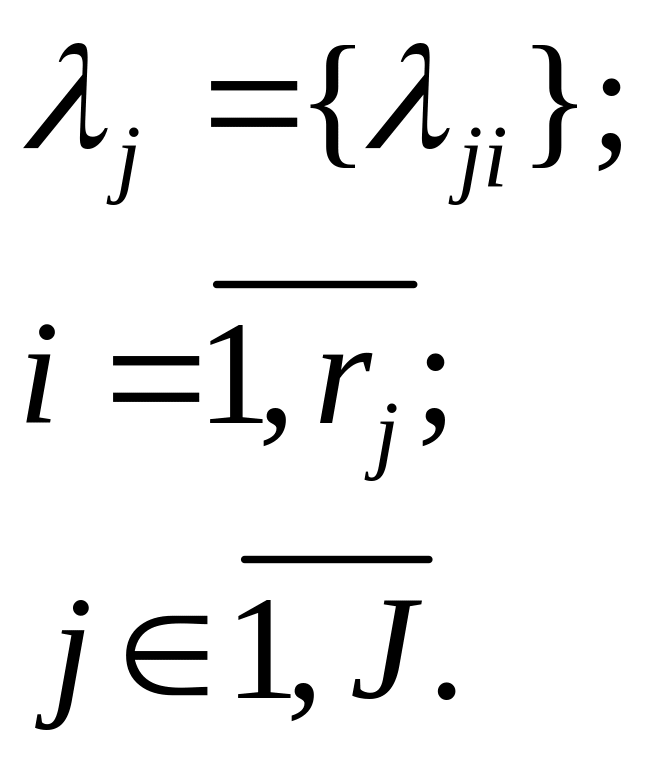
- вектор концепции.

Задаются значения допустимых затрат для j-ой подсистемы:

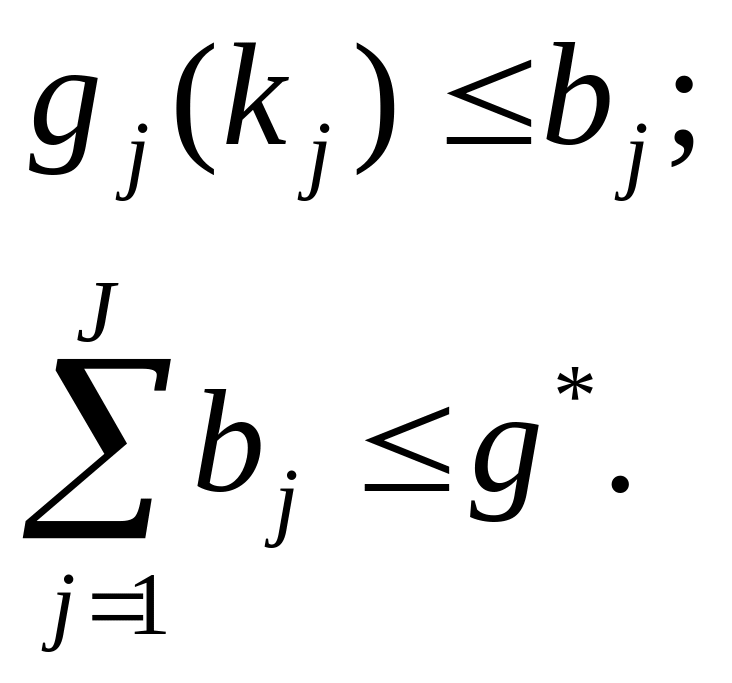
(3)

при условии

Экстремальное значение является функцией выделенного ресурса для j-ой подсистемы.

При фиксированном векторе концепций , оптимальным является вектор:

(4)

Вектор является эффективной альтернативой на множестве ЦФ и его значение зависит от выделенного ресурса j-ой подсистемы и вектора концепций .

Таким образом, оптимальное решение для j-ой подсистемы принадлежит множеству Парето, построенному на функционалах . Само множество Парето зависит от параметра .

2. Варьируя вектор 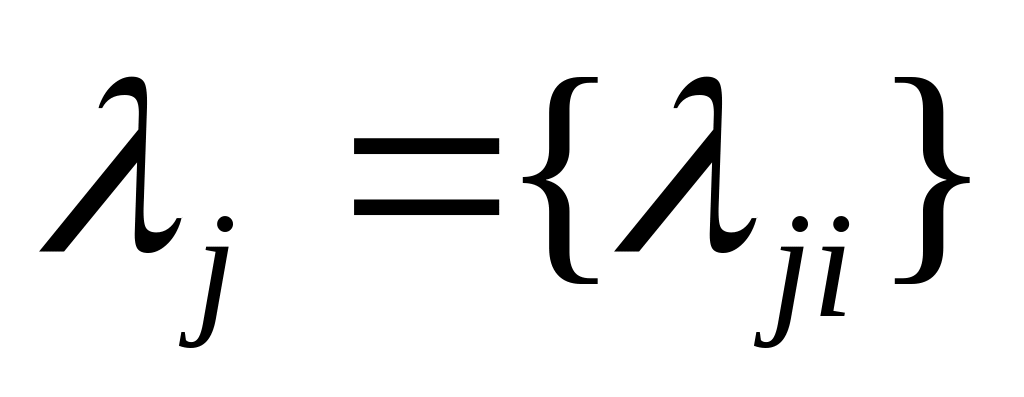, 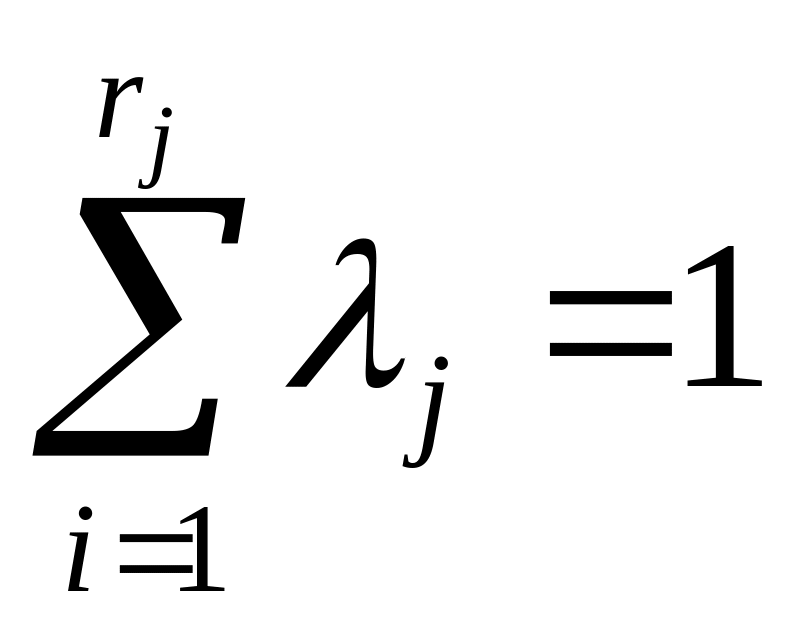и значение ресурса 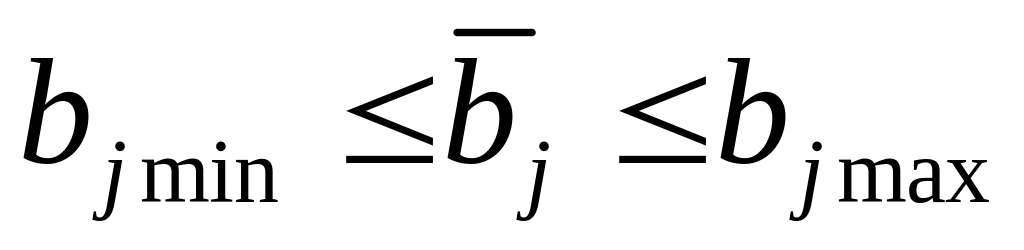, т.е.

и определяя для этих значений точки , удовлетворяющие условиям (3), (4), мы получим все точки множества Парето для j-ой подсистемы и соответствующего вектора оптимальных значений вектора конструктивных параметров.

Таким образом, предположение о том, что функционалы достаточно полно характеризует облик подсистемы, приводит к тому, что облик СТС в целом следует искать среди точек Паретовских множеств:

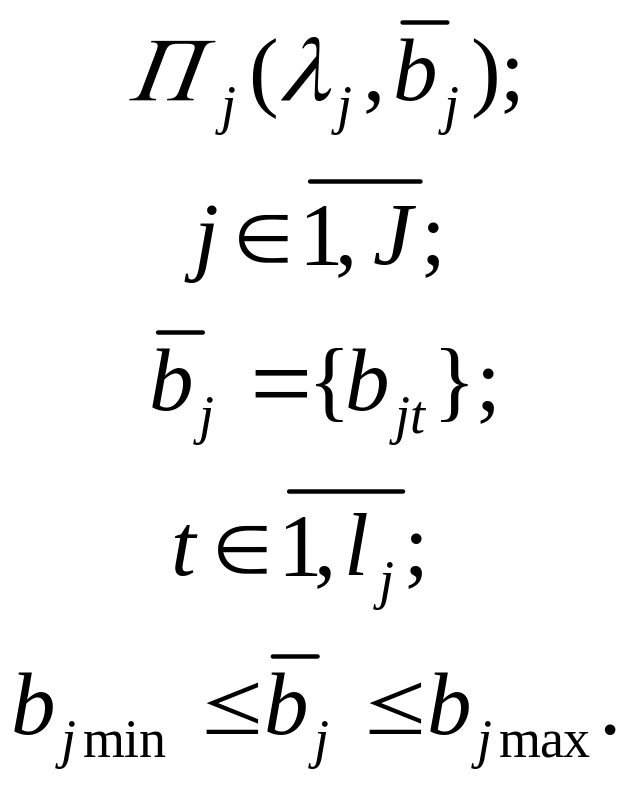
3. Глобальный критерий эффективности системы в целом оптимизируется на множестве Парето

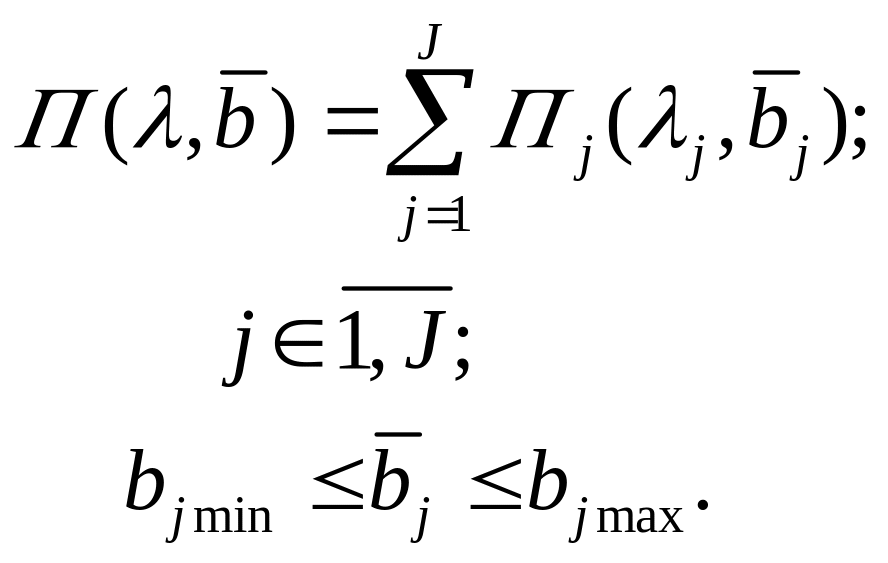
, -верхние и нижние ограничения на ресурс, выделяемый j-ой подсистеме.

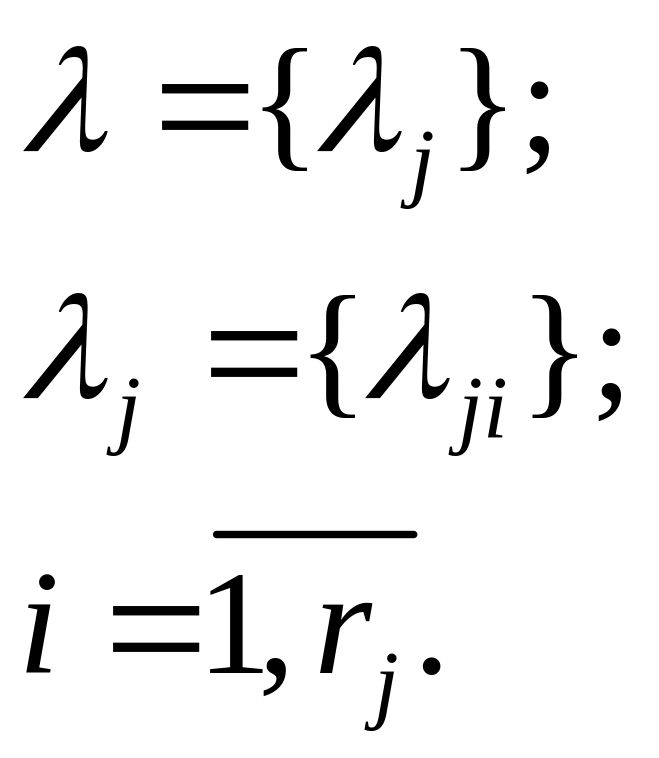
Необходимо выполнить:

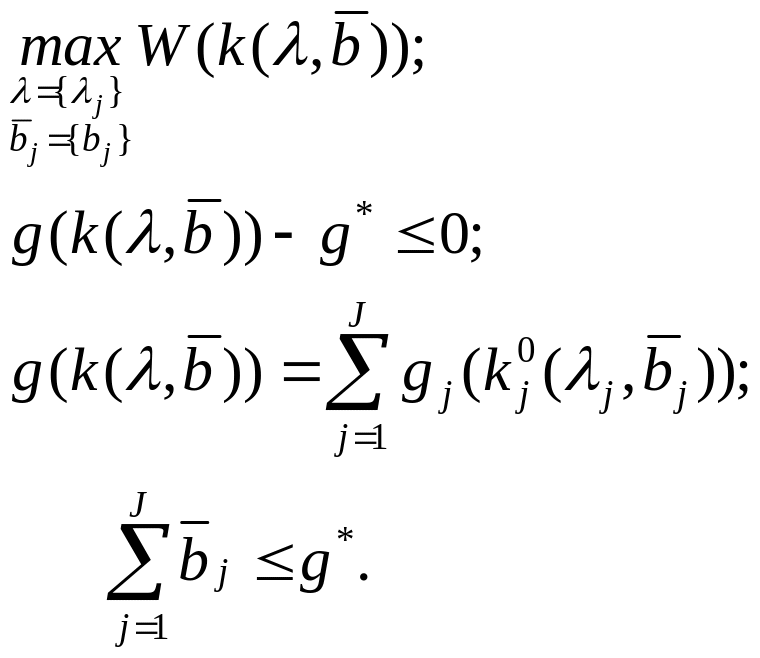(5)

Таким образом, в результате решения задачи (5) производится оптимальное распределение вектора ресурса по подсистемам для заданного на дискретном множестве значений вектора , и выбор из условия

,

где

По оптимальному значению из множества определяются оптимальные вектора

для каждой подсистемы .

Таким образом, процесс проектирования с использованием данного подхода направлен снизу-вверх и включает два этапа:

на первом этапе выполняется решение J локальных задач оптимизации 4 по частным критериям при фиксированных, задаваемых на дискретном множестве значениях ресурсов, выделяемых каждой подсистеме системой. В результате для каждой подсистемы определяются области Парето за счет вариаций значений вектора и ограничений на допустимый ресурс . Полученные для каждой подсистемы множества Парето зависят от выделенного ресурса, который задавался на допустимом дискретном множестве для каждой подсистемы.

На втором этапе производится поиск оптимального вектора конструктивных параметров системы в целом задачи (5) по глобальному критерию на множествах, оптимальных по Парето решений, для каждой из j подсистем, выделенных на первом этапе. Решение на этом этапе состоит в определении оптимального вектора концепции и оптимального распределения вектора ресурса по j подсистемам.