П. (7.2) Общие свойства конформных отображений

Опред. w=f(z) обл. D, расширенной комплексной плоскости z на области G комплексной плоскости W наз. конформным, если:

1 Это отображение взаимно однозначно, т.е. функция f(z) одноместна в области D.

2 Функция f(z) регулярная в области D за исключением может быть 1-й точки, в которой эта функция имеет полюс 1-ого порядка. Из геометрического смысла производной вытекает следующие свойства конформности отображения :

а) Постоянство растяжений: линейное растяжение в точке z₀ одинаково для всех кривых проходящих через эту точку и равно |f’(z₀)|

б) Сохранение углов. Все кривые в точке z₀ поворачиваются на одинаковый угол равный: arg f’(z₀)

в) Отображение обратных конформных отображений также является конформным

г) Суперпозиция 2-х конформных отображений также является конформным отображением

Определение: углом между прямыми и принадлежащих бесконечности проходящих через точку z=∞ называются углом между образами этих кривых при отображ. : 𝜉= , 𝜉=0

д) При конформных отображениях область D расширяются комплексные плоскости сохраняя углы между кривыми в каждой точке этой области.

Пусть D и G ограниченные односвязные области границами которой являются простые замкнутые кусочно гладкие кривые и соответственно. Тогда имеет место следующая теорема:

Т. (7.4а) Принцип соответствия границ

Если функция w=f(z) конформное отображение области D, на область G то:

1 Функцию можно непрерывно продолжить на замыкание области D, т.е. можно доопределить f(z) на так, что получится непрерывная в D функция.

2 Эта функция w=f(z) отображает взаимооднозначную кривую с сохранением ориентации.

Т (7.5) Критерии одно местности функции в области

Пусть функция w=f(z) регулярна в области D и непрерывна вплоть до её границ . Отображение взаимнооднозначной кривой на кривую с сохранением ориентации, тогда эта функция однозначна в области D и отображ. конформн. области D на область G.

Важнейшей теоремой конформности отображения является следующая теорема:

Т (7.6) Теорема Римана

Пусть D односвязная область расширенной комплексной плоскости, границы которой состоит более чем из одной точки, тогда:

1)Существует функция w=f(z),которая конформно отображает область D на круг: |w|<1.

2)Эта функция единична, если выполняется условие: f( arg f’(z)=α.

Здесь заданные точки, α-заданное действительное число. Исключениями являются следующие области:

а)Вся расширенная комплексная плоскость.

б) Вся расширенная комплексная плоскость с одной выколотой точкой.

Эти области нельзя конформно отобразить на круг |w|<1.

Следствие: Пусть границы однолистных областей состоят из более чем из одной точки, тогда существует одна и только одна функция w=f(z),которая конформно отображает область Д на область G так, что: f( )= , arg f’( (7.1) ,

Замечание: Вместо единичного круга можно взять другую каноническую область, например верхнюю полуплоскость. Вместо условия (7.1) можно взять другую, содержащую три независимых параметра. Например:

1)Существует единичное конформное отображение w=f(z) обл. Д на область G удовлетворяющую условию f( где - внутренние, а , - внешние точки областей D и G.

2) Существует единичное конформное отображение обл. Д на область G удовлетворяющую условию: f( ; где - различные граничные точки Д, а - различные граничные точки G.

П(7.3) Примеры конформных отображений.

Определение: Функция называется дробно-линейной.

Условие отмечает, что: w(z)≠const,

*Если C≠0, то w(∞)=

*Если C=0, то w(∞)=∞, значит, дробно-линейная функция определена на расширенной плоскости при C=0- функция является линейной.

Т(7.7)Дробно-линейная функция конформно отображает расширенную комплексную плоскость на расширенной комплексной плоскости.

Т(7.8)Совокупность дробно-линейных отображений образуют группу, т.е. выполняется следующее свойство:

1)Супер позиция или производная дробно-линейных отображений является дробно-линейным отображением.

Определение: Точки М и называются симметричными относительно окружности: ɣ:|z-a|=R, если они лежат на одном луче, выходящем из точки а и |z-a|·| = ; Точка z=∞ считается симметричной относительно окружности ɣ с точкой а – центром этой окружности: (7.3) Дробно-линейные отображения обладают следующим свойством сохранения симметрии:

Т(7.9) При дробно-линейном отображении пара точек симметрично относительно окружности переходящей в пару точек симметричных относительно образа этой окружности.

Т(7.10)Существуют дробные отображения при которых три различные точки переходят в другие различные точки , т.е.: (7.4)

Следствие: Функция f(z) определена формулой (7.4) конформно отображённый круг, граница которого проходит через точку , граница которого проходит через точку (к=1,2,3)

*Дробно-линейное отображение переводит точку в точку а точка в точку =∞: общий вид (7.5) где А принадлежит множеству комплексных чисел.

* Дробно-линейное отображение Im z>0→|w|<1 полуплоскость на круг |w|<1 имеет вид: , Im (7.6)

Дробными отображениями плоскость Im →|w|<1(круг) так, что: w( =0. В силу сохранения симметрии, если →0, то w( И по формуле (7.5): w=A (7.7.)

Докажем, что |A|=1. Точки действительной оси переходит в точки единичной окружности |w|=1, при z=xϵR, значит из (7.7) получаем: 1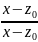=|A | =|A|| . Значит А= и получаем что из (7.7) следует (7.6). Рассмотрим свойства функции w= . Эта функция однолистна в области Д, только тогда, когда в этой области нет точек и таких, что: = .