П(7.1) Локальные свойства отображения регулярных функций
Рассмотрим
случай, когда f’(
Т(7.1)
Пусть функция w=f(z)-
регулярна в
≠∞,
f’(
Существует окрестность u
и v
;
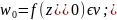Свойственно, что существует функция
z=ψ(w),
такая, что:
А)f(z)=w и для любых wϵv, w≠ имеет равно и различно регулярная, принадлежащая u, z=ψ(w)ϵV;
Б)
z=ψ(w)
аналитическая в области V.
w≠
f(ψ(w))=w,
wϵv.
Пусть f(z)
аналитическая в кольце: k:0<|z-a|<ρ.
И пусть в каждой точке этого кольца имеем u различным элементам f(z), тогда m, а изолированная точка ветвления порядка n функция равна (z). Аналогично вводится порядок m ветвления z=∞.
Следствие
(1): При введении
условия Т(7.1)точка
является алгебраической, т.е. конечного
порядка точка ветвления нормальна и
для функции: z=ψ(w)
для обратной w=f(z)
и в окрестности точки
имеет место разложение в ряд: ϕ(w)=
Следствие
(2): При условии
теоремы (7.1) существует функция z=g(ξ),
регулярна
в точке ξ=0 и такая, что f(g(ξ))=f(z)+
в окрестности ξ=0 при этом: g’(0)=
Введём понятие однолистной функции в точке :
Функция f(z) – однолистна в точке , если эта функция однолистна в некоторой точке . Однолистная функция является однолистной в каждой точке. Обратное неверно- однолистность функций может быть неоднолистно в окрестности.
Т(7.2)
f(z)-
регулярна в
≠∞,
является однолистной тогда, когда f’(
Следствие
(3): f(z)=
|z|>
R
Регулярна в точке
≠∞,является
однолистной в этой точке тогда, когда
вычет не равен нулю.
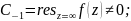
Следствие (4): f(z) имеет полюс, в точке конечный или бесконечный, является однолистной в этой точке тогда, полюс простой( первого порядка).
Итог:
Пусть f(z)
– регулярна и однолистна в области Д с
выколотыми точками: D\{
,
,..,
}.
Среди точек
(к=Т,n).
Не может быть существенно особых точек и не может быть двух полюсов. Значит f(z) может иметь один полюс первого порядка. Необходимое условие однолистной функции f(z) в области D. f(z)-однолистна в Д:
1)f(z) – регулярна в области Д за исключением первой точки –простого полюса.
2)В каждой точке регулярной |z|ϵD должно выполняться условие f’(z)≠0.
3)Если
точка z=∞ϵD
в этой точке f(z)
регулярно, то должно быть:
Эти условия не достаточны для однолистности функций в области.
Т(7.3) Принцип сохранения области. Пусть f(z) – регулярна в области Д и f(z)≠const. Тогда w=f(z)- образованная область является областью.
Следствие(5): Пусть функция f(z) регулярна а области Д расширенная комплексная плоскость за исключением полюсов f(z)≠const.
Тогда образованная область D при отображении w=f(z) является расширенной комплексной плоскостью.
Т(7.4) Принцип максимума модуля. Пусть f(z) регулярна в ограниченной области Д неприрывна в данной области и f(z)≠const тогда и максимум модуля: max|f(z)|, zϵD.
Следствие(6): Если f(z)≠const регулярна в области Д, то модуль |f(z)| не может иметь локальный максимум во внутренних точке области Д.
Следствие(7): Если регулярное в области Д f(z)≠const, не имеет нулей в области Д, то |f(z)| не может иметь минимум в точке области Д.
Теорема Лема Шварца
Пусть
функция f(z)
регулярна в круге: |z|<1,
f(0)=0:
|f(z)|<1
при |z|<1.
Тогда во всем круге |z|<1
имеет место неравенство: |f(z)|≤|z|,
если хотя бы в одной точке |z|≠0
круга |z|<1выполняется
равенство: |f(z)|=|z|,
то f(z)=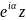
,
α∊R