Тема: Оценка интеграла.

Лема(2.1): Пусть функция f(z) интегрируема на прямой ɣ , тогда имеет место оценка:

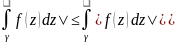| (2.8)

|dz|=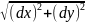 =ds , ds-элемент длинны кривой ɣ.

Следствие: | |≤Mι(ɣ) (2.9) где M=max |f(z)|, l(ɣ)

П(2.2) Примеры непрерывных функций комплексной переменной.

Определение: Число A называются по множеству Е, zϵЕ, если для любого ε>0, существует такое δ(ε)>0 что для всех δϵЕ выполняется условие: 0<|z- |<δ, выполняется следующее неравенство: |f(z)-A|<ε

Существование

A=α+βi равносильно существованию двух пределов:

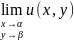и

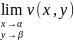
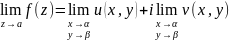
Определение: Функция f(z) называется непрерывный в точке а, если для любого числа ε>0, существует такое δ>0, что для всех εϵЕ, удовлетворяют условию: |z-a|<δ следовательно |f(z)-f(a)|<ϵ.

Это определение равносильно тому что, u(x,y) и v(x,y), непрерывные в точке (α;β).

Свойства непрерывных функций:

Если f(z) и g(z) непрерывны в точке =а, то:

1)f(z)±g(z)-непрерывные при С принадлежит множеству комплексных чисел.

2)f(z)*g(z)-непрерывны

3) –непрерывны, если g(a)≠0

4)g(f(z))-непрерывные, если g(w)- непрерывны w=f(a)

Пример(1): a(z)+b, Re z, Im z, |z|, – непрерывные на всей комплексной плоскости т.е. неприрывны в любой точке

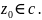
Пример(2):P(z)= – многочлен с комплексными коэффициентами, являющийся неприрывной функцией на всей комплексной плоскости.

Пример(3):R(z)= 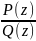–рациональная функция, где p(z) и Q(z) –многочлены. Неприрывны во всех точках комплексной плоскости, в которой Q(z)≠0.

Функция f(z) определенная на множестве Е называется равномернонеприрывной на множестве Е, если для любого ε>0 существует такое δ>0, такое что |f(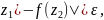 для любых

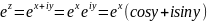
Свойства:

1.

2.

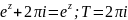
3. непрерывна во всей комплексной плоскости

4.| |=

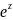5.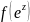 принимает все значения, кроме нуля даются формулой: , k=0, (2.10)

Если k=0,

Если =А, то комплексное число z называют log комплексного числа А, А≠0 и обозначают lnA

Из (2.10) следует ,что lnA=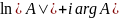

Ln1= , ln(-1)=(2k+1)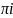

Тригонометрические функции.

Sinz и cosz определяются следующими формулами:

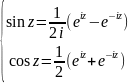(2.11)

Свойства:

1.Функции Sinz и cosz непрерывны во всей комплексной плоскости.

2.Функции Sinz и cosz принимают все значения, т.е. Sinz=А имеют решения , cosz=А комплексного числа А.

3. Формулы элементарной тригонометрии справедливы для всех zϵC

Sin(

Sinz=2sinzcosz;

Sin(z+2π)=sinz, cosz(z+2π)=cosz; Sin(-z)=-sinz; cos(-z)=sinz;

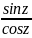tgz= ; ctgz= ;

shz=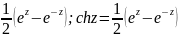

shz=-isin(iz); sh=cos(iz);

П(2.3) Интегральная форма Коши

Определение: Область D, называется односвязной, если две любые её точки можно соединить отрезком целиком лежащим в области D.

Т(2.2) Если область D односвязная, то для того чтобы интеграл по ɣ: по любой замкнутой кривой ɣ лежащей в области D равнялся нулю, необходимо и достаточно, чтобы во всей области D выполнялась равенство:

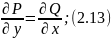
Т(2.3) Пусть функция f(z)-дифференцирована в односвязной области D и её производная неприрывна в D тогда интеграл 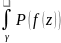по любой замкнутой кривой ɣ лежащей в области D равен нулю.

Доказательство:

Если f(z)=u(x,y)+iv(x,y)

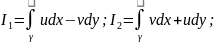
Т.к. f(z) имеет непрерывную производную в области D, то частная производная первого прядка функций u и v неприрывны в области D и выполняется условие Коши-Римана:

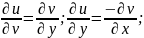Ч.т.д.

В силу теоремы (2.3)

Т(2.4)(интегральная теорема Коши):

Пусть функция f(z) дифференцируема в односвязной области D, тогда интеграл от f(z) по любой замкнутой кривой ɣ лежит в области D=0;

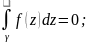
Замечание: Функция f(z)= дифференцируема в кольце 0<|z|<2;

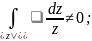
Это пример показывает, что требование односвязной области теоремы Коши существенно.

Следствие(1):

*Если функция f(z) дифференцируема в односвязной области D, то интеграл от f(z) не зависит от пути интегрирования.

*Если кривые лежат в области D имеют общее начало и конец, то интеграл

Это значит, что кривую ɣ можно деформировать в область D оставляя концы неподвижными при этом интеграл не меняется.

Определение: Такие кривые называются гамматопными, когда одну из них можно получить неприрывной деформацией другой.

Т(2.5) Если функция f(z) дифференцируема в области D, а кривые голомофобны в области D, то Область D может быть не односвязной.

Определение: Кривая называется гладкой, если её уравнение можно записать в виде:

z=δ(t), α≤t≤β, где δ’(t), tϵ[α,β], δ’(t)≠0. Причём если α=β, то δ’(α)≠δ’(β);

Определение: Кривая называется кусочногладкой, если её можно разбить на конесное число гладких кривых.

Теорема Коши остаётся в силе, когда кривая ɣ является границей в области D.

Т(2.6) Пусть D ограниченная односвязная область кусочногладкой границы ɣ и пусть функция f(z) дифференцируема в области D и неприрывна вплоть до её границы, тогда:

Следствие(2): Пусть граница ɣ многосвязной области D состоит из замкнутой кусочногладкой кривой и попарно не пересекающей замкнутой кусочногладкой кривой расположенной внутри . И пусть функция f(z) дифференцируема в области Dнеприрывна вплоть до её границы, тогда:

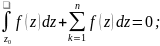
Кривые 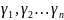ориентированы так, что при обходе каждый из этих кривых области D остаётся слева, такое направление обхода называется положительным.

Определение: Пусть функция f(z) определена в области D, дифференцируема в этой области, а функция F(z) дифференцируема, если:F’(z)=f(z), zϵD, то F(z) первообразная функции f(z) в области D.

Т(2.7) Пусть функция f(z) дифференцируема в односвязной области D, то она имеет в этой области- первообразную. (2.15)

Если F(z) первообразная f(z)+C, также будет первообразной f(z) справедлива о обратное.

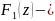Т(2.7) Совокупность всех первообразных в области D определяется формулой: (z)+C, где какая-нибудь первообразная f(z), а С- произвольная константа.