
- •Непрерывность и дифференцируемость комплексных переменных
- •П1.1 Предел последовательности комплексных чисел.
- •Свойства аналитической функции:
- •Тема 2: Интегрируемые теоремы. Интегральная форма
- •Свойства интегралов:
- •Тема: Оценка интеграла.
- •Свойства непрерывных функций:
- •Доказательство:
- •Доказательство:
- •Доказательство:
- •П(7.1) Локальные свойства отображения регулярных функций
- •Теорема Лема Шварца
- •П. (7.2) Общие свойства конформных отображений
- •Преобразование Лапласа.
- •Свойства преобразований Лапласа:
- •9) Изображение свёртки.
- •Метрические и топологические пространства.
- •Мера, интеграл Лебега
Доказательство:
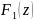 и
и

F(z)=
Значит,
в силу (1.9):

По теореме из мат.
анализа: если все частные производные
равны нулю: F(z)=const
следует

Следствие(3):
При условии теоремы(2.7) любая первообразная
F(z) функции
f(z) выражается
формулой: F(z)= комплексным
числам.
комплексным
числам.
Следствие(4):
При условии теоремы(2.7) имеет место
формула Ньютона-Лейбница:
 (2.17)
(2.17)
Доказательство:
В (2.16) z= F(
F( ч.т.д.
ч.т.д.
Следствие(5):
Если функции f(z)
и g(z)удовлетворяют
условию теоремы (2.7), то справедлива
формула интеграла по частям:
 (2.18)
(2.18)
Интеграл от элементарных функций считаем по тем же методам и формулам, что и в случае действительной переменной.
П(2.4)Интегрируемая формула Коши
Из интегр. теоремы Коши вытекает одна из важнейших формул теории функций комплексной переменной интегрируемая формула Коши
Т(2.9) пусть
функция f(z)
дифференцируема в односвязной области
Д и пусть простая замкнутая кривая
 и
ориентирована положительна, тогда в
любой точке z
лежащей внутри ɣ справедлива формула:
и
ориентирована положительна, тогда в
любой точке z
лежащей внутри ɣ справедлива формула:
 (2.19) Эта формула
называется интегрирующей формулой
Коши.
(2.19) Эта формула
называется интегрирующей формулой
Коши.
Замечание
1: Пусть Д ограниченная односвязная
область с кусочногладкой границей и
пусть функция f(z)
дифференцируема в области Д и непрерывна
вплоть до её границы, тогда для любой
точки z лежащей внутри Д
имеет место формула:
Эта формула остаётся в силе и в том
случае, когда Д – многосвязная область.
и
пусть функция f(z)
дифференцируема в области Д и непрерывна
вплоть до её границы, тогда для любой
точки z лежащей внутри Д
имеет место формула:
Эта формула остаётся в силе и в том
случае, когда Д – многосвязная область.
Замечание
2: Если в правой части
формулы (2.19) z
не принадлежит кривой
 ,
т.е. z лежит вне замыкания
Д, то подынтегральная функция
дифференцируется по
,
т.е. z лежит вне замыкания
Д, то подынтегральная функция
дифференцируется по
 всюду в Д и по теореме Коши интеграл
равен нулю, значит:
всюду в Д и по теореме Коши интеграл
равен нулю, значит:

Т.(2.10) теорема о среднем
Пусть
функция f(z)
дифф. в круге К, тогда значение этой
функции в центре круга равна среднему
арифметическому значений этой функции
на окружности
 (2.21)
(2.21)
Ряды Тейлора и Лорана
Ряд Лорана позволяет раскладывать функцию больше К круга (z-1)
П.3.1 Степенные ряды
Определение: Степенным
рядом называется ряд вида: (3.1), где a,
(3.1), где a, заданные
комплексные числа, z-комплексная
переменная. При а=0, формула имеет вид
заданные
комплексные числа, z-комплексная
переменная. При а=0, формула имеет вид
 (3.2)
(3.2)
Свойства ряда (3.2) справедливы и для (3.1)
Определение: Областью сходимости степенного ряда (3.2) называется множество всех точек z, в которых (3.2) сходится. Ряд всегда сходится в точке z=0
Теорема
Абеля: Если степенной ряд сходится
в точке
 ,
то он абсолютно сходится в круге
,
то он абсолютно сходится в круге
 |z|
|z| |
|,
а в любом меньшем круге
|
|,
а в любом меньшем круге
 :
|z|
:
|z| |
|
этот ряд сходится равномерно.
|
|
этот ряд сходится равномерно.
Следствие(1): Ряд
(3.2) сходится в круге k|z|<R,
а в любом меньшем круге |z| этот ряд сходится равномерно. Круг к –
называется кругом сходимости, а его
радиус R – радиусом
сходимости(3.2). В точках окружности |z|=R
ряд (3.2) может сходиться, а может и
расходиться, если ряд сходится только
при z=0, тогда R=0.
Если на всей плоскости, то R=∞.
Радиус сходимости ряда (3.2) определяется
по формуле Коши-Адамара: R=
этот ряд сходится равномерно. Круг к –
называется кругом сходимости, а его
радиус R – радиусом
сходимости(3.2). В точках окружности |z|=R
ряд (3.2) может сходиться, а может и
расходиться, если ряд сходится только
при z=0, тогда R=0.
Если на всей плоскости, то R=∞.
Радиус сходимости ряда (3.2) определяется
по формуле Коши-Адамара: R=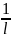 ,
,
 (3.3)
(3.3)
Т(3.2) Пусть радиус сходимости степенного ряда f(z)=R, тогда этот ряд можно почленно дифференцировать в круге |z|<R любое число раз, получим степенные ряды, которые имеют тот же радиус сходимости, что и ряди(3.2).
Следствие(2):
Коэффициент n
степенного ряда f(z)=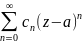 (3.4a)сходится
в круге k:|z|<R,
(k≠0)определена
формула:
(3.4a)сходится
в круге k:|z|<R,
(k≠0)определена
формула: (3.5) n=1,2,3…
(3.5) n=1,2,3…
Определение:
Степенной ряд
 Тейлора функции f(z).
Всякий степенной ряд(3.4а) в круге
сходимости есть ряд Тейлора его сумма
f(z).
Тейлора функции f(z).
Всякий степенной ряд(3.4а) в круге
сходимости есть ряд Тейлора его сумма
f(z).
П(3.2) Свойства регулярных функций.
Понятие регулярной функции является одним из основных понятий ТФКП.
Определение:
Пусть функция f(z)
определены в окружности точки z=a,
a≠∞
и разлагается в ряд: f(z)= сходится в некоторой окрестности точки
z=a
т.е. в круге|z-a|<ρ,
тогда функция f(z)
называется регулярной в точке z=a.
Функция f(z)
называется регулярной в области D,
если она регулярна в каждой точке этой
области.
сходится в некоторой окрестности точки
z=a
т.е. в круге|z-a|<ρ,
тогда функция f(z)
называется регулярной в точке z=a.
Функция f(z)
называется регулярной в области D,
если она регулярна в каждой точке этой
области.
Т(3.3) Для того чтобы, функция f(z), регулярна в области D, необходимо о достаточно, чтобы она была дифференцируема в этой области.
Т(3.4) Если
функция, дифференцируема в этой области,
то она бесконечно дифференцируема имеет
место формула:

Где
 граница
круга |𝜉-z|∊P
лежит в области D.
граница
круга |𝜉-z|∊P
лежит в области D.
Критерии регулярности функции в области D:
1)Дифференцируемость функции в области D
2)Условия Коши-Римана.
Свойства регулярной функции:
1.f+g,
f-g,
f*g,
 регулярные функции, если f
и g
регулярны.
регулярные функции, если f
и g
регулярны.
2.Регулярная функция бесконечно дифференцируема.
3.Для регулярной функции справедлива интегрируема теорема Коши и интегральная Форма Коши.
4.Первообразная регулярной односвязной функции- регулярна.
Всякая
функция f(z)регулярна
в круге |z-a|<ρ
разлаживается в этом круге в степенной
ряд: f(z)=
где:

Этот
степенной ряд называется рядом Тейлора.
Вычислив производные получим следующие
производные:


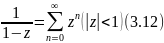
Обычно коэффициенты ряда считают, не по (3.8), а используют (3.9-3.12).
Некоторые приёмы разложения:
1)Арифметические операции: пусть f(z)=
g(z)= в круге |z-a|<R;
Aˑf(z)=


2)Метод неопределённых коэффициентов
g(z) ,
h(z)=
,
h(z)= f(z)=
f(z)=
f(z)=
Приравниваем коэффициенты при одинаковых степенях разности (z-a) в равенстве:
f(z)*h(z)=g(z)
получим:

3) Переразложение степенного ряда
Пусть ряд f(z)= сходится в круге k: |z-a|<R (3.18)
z-a=(b-a)+(z-b) (3.19)
Из (3.18) и
(3.19) имеем f(z)= (3.20)
(3.20)
где
|z-b|< ,
ρ=R-|b-a|,
тогда |z-a|<R,
перераскладывая ряд (3.20) имеем:
,
ρ=R-|b-a|,
тогда |z-a|<R,
перераскладывая ряд (3.20) имеем:
f(z)= (3.21)
сходится в круге |z-b|<
(3.21)
сходится в круге |z-b|<
Определение:
Точка z=a
называется нулем регулярной функции
f(z)
, если f(a)=0
и если f(z)= (3.22)
т.е.
(3.22)
т.е.
 ,
то m
называют порядком или кратностью нуля,
z=a
функции f(z).
,
то m
называют порядком или кратностью нуля,
z=a
функции f(z).
Порядок нуля z=a функции f(z) равен наименьшему порядку производной этой функции отличной от нуля при z=a.
Т(3.5) Точка
a≠∞
тогда и только тогда является нулём
порядка m
функции f(z),
когда эта функция представлена в виде:
 где
h(z)
регулярна в точке a,
где h(a)≠0
где
h(z)
регулярна в точке a,
где h(a)≠0
Определение:
Пусть f(z)
= регулярна в z=∞.
Z=∞
регулярна в z=∞.
Z=∞
Т(3.6) Пусть
функция f(z)
регулярна в точке А и f(A)=0,
тогда либо f(z)≡0
в некоторой окрестности точки А, либо
существует такая окрестность точки А,
в которой нет нулей функций f(z),
f(z)≠0,
zϵ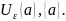
Это значит, что нули регулярной функции изолированы.
П(3.3) Ряд Лорана
Определение: Ряд
вида (3.23) , где a фиксированная
точка комплексной плоскости,
(3.23) , где a фиксированная
точка комплексной плоскости,
 -заданные
комплексные числа называются рядом
Лорана. Этот ряд называется сходимым в
точке z, если в этой точке
сходятся ряды:
-заданные
комплексные числа называются рядом
Лорана. Этот ряд называется сходимым в
точке z, если в этой точке
сходятся ряды:
(3.24)
 (3.25)
(3.25)
Из суммы ряда (3.23)
равна сумме рядов (3.24) и (3.25). Ряд (3.24)
сходится в круге: |z-a|<R,
а ряд (3.25) сходится при
 .
Если
.
Если
 то
ряд сходится в кольце:
то
ряд сходится в кольце:
 В каждой точке вне этого кольца ряд
расходится в силу расходимости одного
из этих рядов (3.24) или (3.25)
В каждой точке вне этого кольца ряд
расходится в силу расходимости одного
из этих рядов (3.24) или (3.25)
Т(3.7)Функция
f(z) регулярна
в кольце Д:
представляется в этом кольце рядом
Лорана:
,
где
= (3.26a)
n=0,±1,±2…
(3.26a)
n=0,±1,±2…

Т(3.8) Разложение в ряд Лорана функции f(z) регулярна в кольце Д: и единственна. Из этой теоремы следует, что коэффициент не зависит от того, как получено это разложение.
Т(3.9) Пусть функция
f(z) регулярна
в кольце Д: ,
тогда коэффициент ряда Лорана f(z)=
удовлетворяет неравенство: |
,
тогда коэффициент ряда Лорана f(z)=
удовлетворяет неравенство: | n=0,±1,±2… , а M-max
|f(z)|;
n=0,±1,±2… , а M-max
|f(z)|;
 |z-a|=R,
zϵ
.
|z-a|=R,
zϵ
.

Многозначные функции.
П (4.1) Обратные функции
Пусть функция w=f(z)
определена на множестве
 .
Е-область значения. Тогда для каждого
значения wϵ
.
Е-область значения. Тогда для каждого
значения wϵ существует одно или несколько значений
z из E таких
что: f(z)=w
(4.1)
существует одно или несколько значений
z из E таких
что: f(z)=w
(4.1)
Эти решения определяют функцию: z=h(w) называется обратной функцией к w=f(z)
Т(4.1)(об
боратной функции): Пусть функция w=f(z)
регулярна в точке
и пусть
 тогда:
тогда:
1)Существует
круг k:|z-
|<ρ
и круг
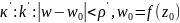 ,
таким что, для каждого
,
таким что, для каждого
 из
из
 уравнения (4.1) имеет единственное решение:
z=h(w),
zϵk.
уравнения (4.1) имеет единственное решение:
z=h(w),
zϵk.
2)Функция
z=h(w)
обратна к функции w=f(z)
и регулярна в точке

3)В некоторой
окрестности точки
 :
:

П(4.2) Функция lnz.
Логарифмическую
функцию в комплексной плоскости
естественно ввести, как обратную к
f(w)= (4.3)
z=r
(4.3)
z=r ,
тогда из (4.3) можно найти: u=lnr,
v=ϕ+2kπ,(k=0,±1,±2…),
значит w=ln|z|+i(argz+2kπ)(4.4)
где аргумент z
фиксирует значение аргумента числа к,
к-целое число. Это значит, что уравнение
(4.3) имеет бесконечно много решений(4.4)
т.е. задаёт многозначную функцию.
Попытаемся выделить в области Dоднозначную
непрерывную ветвь ln
т.е. неприрывную функцию значение которой
в точке из области D
совпадает с одним из значений многозначной
функции lnz
т.е. выделим ветвь. Возьмём в качестве
D
область
,
тогда из (4.3) можно найти: u=lnr,
v=ϕ+2kπ,(k=0,±1,±2…),
значит w=ln|z|+i(argz+2kπ)(4.4)
где аргумент z
фиксирует значение аргумента числа к,
к-целое число. Это значит, что уравнение
(4.3) имеет бесконечно много решений(4.4)
т.е. задаёт многозначную функцию.
Попытаемся выделить в области Dоднозначную
непрерывную ветвь ln
т.е. неприрывную функцию значение которой
в точке из области D
совпадает с одним из значений многозначной
функции lnz
т.е. выделим ветвь. Возьмём в качестве
D
область
 –плоскость с разрезом от (0;+∞); В этой
области функция ϕ=argz
допускаем выделение однозначных ветвей.
Пусть argz-
однозначная ветвь, при ϕϵ2π: 0<ϕ<2π;
w=lnz=ln|z|+iargz(4.4a)
–плоскость с разрезом от (0;+∞); В этой
области функция ϕ=argz
допускаем выделение однозначных ветвей.
Пусть argz-
однозначная ветвь, при ϕϵ2π: 0<ϕ<2π;
w=lnz=ln|z|+iargz(4.4a)
Это уже однозначная и неприрывная функция в области функция w=ln взаимно однозначное отображение области на полосу:0<Im<2π
По теореме (4.1) функция
f(z) определяет
равенство (4.4) регулярна в
.
Она называется ветвью в области
.
Многозначной логарифмической функцией,
а её производная вычисляется так: (ln
 существует бесконечно много однозначных
непрерывных ветвей аргумента и все они
имеют вид: (arg
z
существует бесконечно много однозначных
непрерывных ветвей аргумента и все они
имеют вид: (arg
z рассматриваемая выше ветвь аргумента.
рассматриваемая выше ветвь аргумента.
При к=1
получим ветвь: arg и соответствует ветвь ln
будет иметь вид: w=|lnz
и соответствует ветвь ln
будет иметь вид: w=|lnz .
При к=-1 получим: w=|lnz
.
При к=-1 получим: w=|lnz (4.7)
(4.7)
Для выделения регулярной ветви логарифма достаточно указать соответствующую ветвь аргумента по формулам (4.5) т.е. выбрать число к. Возьмем в качестве D область с разрезом по лучу: (рис см. в тетр.).
Функция
lnz
распадается на бесконечное число
однозначных ветвей.
 однозначная ветвь аргумента –π<(argz
однозначная ветвь аргумента –π<(argz Вместо того чтоб рассматривать бесконечно
много функций возьмём бесконечно много
листов
Вместо того чтоб рассматривать бесконечно
много функций возьмём бесконечно много
листов
 считать, что область
считать, что область
 задана регулярная функция f(z).
Теперь склеим область
задана регулярная функция f(z).
Теперь склеим область
 поверхность. Пусть
поверхность. Пусть
 и
пусть
и
пусть
 и
и
 берега. Если z=x<0,
то
берега. Если z=x<0,
то

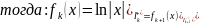 .
.
Склеим
нижний берег
 верхним берегом разряда
верхним берегом разряда
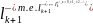 тогда
функция
тогда
функция
 ,будет однозначно полученной одномерной
поверхности. Простроенная поверхность
называется Римановой поверхностью lg.
,будет однозначно полученной одномерной
поверхности. Простроенная поверхность
называется Римановой поверхностью lg.
Теория вычетов и её приложение.
П(5.1) Теорема о вычетах.
Пусть
функция регулярна в кольце k:
0<|z-a|< .Точка
аϵ С, а≠∞ точка а является либо изомер.
Особой точкой однозначного характера
либо точкой регулярности f(z)
расклад в ряд Лорана
.Точка
аϵ С, а≠∞ точка а является либо изомер.
Особой точкой однозначного характера
либо точкой регулярности f(z)
расклад в ряд Лорана
f(z)
Определение:
вычетом функции f(z)
в точке а называется коэффициент
 ряда
Лорана функции f(z)
в окрестности точки т.е.
ряда
Лорана функции f(z)
в окрестности точки т.е. (5.1)
(5.1)
По теореме
(3.7)
 где окружность
где окружность
 :
|z-a|>
|0<
:
|z-a|>
|0< ориентируется положительно:
ориентируется положительно:
 =
= (5.2) Эта
формула часто используется для нахождения
интегралов.
(5.2) Эта
формула часто используется для нахождения
интегралов.
Если
а-простой полюс, то функцию можно
разложить следующим образом
 (5.3)
(5.3)
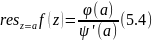
Если
а-полюс порядка m,
для функции f(z),
то ряд Лорана имеет вид:
 (5.5)
(5.5)
Определение:
Вычетом функции f(z)
в точке
 f(z)=
f(z)=
 где окружность
где окружность
 иентированна
отрицательно т.е. обходит
по часовой стрелке.
иентированна
отрицательно т.е. обходит
по часовой стрелке.
Т(5.10) Основная теорема теории вычетов.
Пусть
функция f(z)регулярна
в односвязной области Dза
исключением точек
 -особая
точка, ɣ-простая замкнутая кривая
принадлежащая Д и содержащая внутри
себя
,
тогда:
-особая
точка, ɣ-простая замкнутая кривая
принадлежащая Д и содержащая внутри
себя
,
тогда:
 (5.8)
где ɣ- ориентирована
положительно.
(5.8)
где ɣ- ориентирована
положительно.
Доказательство:
 окружность
достаточно малого радиуса с центром в
точке
окружность
достаточно малого радиуса с центром в
точке
 ориентирована против часовой стрелки.
В силу следующей теоремы (2.6):
ориентирована против часовой стрелки.
В силу следующей теоремы (2.6): используем (5.2) получаем требуемое.
используем (5.2) получаем требуемое.
Следствие:
Пусть функция f(z)
регулярна во всей расширенной комплексной
плоскости за исключением конечного
числа особых точек тогда сумма всех
вычетов функции f(z)
включая точку f=0.
 (5.9)
(k=1,2,3..),az=∞
является либо особой точкой либо точкой
регулярности.
(5.9)
(k=1,2,3..),az=∞
является либо особой точкой либо точкой
регулярности.
Обобщением теоремы (5.1) является следующая теорема:
Т(5.2) Пусть f(z) регулярна в области Д расширенной комплексной плоскости за исключением конечного числа особых точек и непрерывных до границы ɣ этой области.
Пусть ɣ состоит из конечного числа ограниченных кусочно-гладких кривых, тогда:
А)Если
область Д не содержит точку z=∞,
то
 (5.10)
(5.10)
Б)Если
точка z=∞ϵD,
то: то
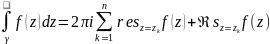 (5.11)
Здесь
все
конечные особые точки функции f(z)лежащей
в области Д.
(5.11)
Здесь
все
конечные особые точки функции f(z)лежащей
в области Д.
П(5.2) Вычислим определение интервалов с помощью вычетов.
Многие определения интеграла от действительной переменной не получается вычислить обычными методами, но их вычисления можно свести к вычетам комплексной функции.
Интегралы
вида: I= (5.12)
R-рациональная
функция.
(5.12)
R-рациональная
функция.
Замена:
z= ;
;
Sinϕ= cosϕ=
cosϕ= dϕ=
dϕ=
При изменении ϕ до 2ϕ: ϕϵ[0,2π], |z|=1, z-пролегает |z|=1 в положит. Интеграл (5.12) сводится к интегралу:
1)I=
 ;
I=2πi
;
I=2πi
2)Интегралы
от рациональных функций: ; I= .
.
Т(5.3) Пусть
функция f(z)
регулярна в области Im
z>0
за исключением конечного числа особых
точек и неприрывна вплоть до границы
это области. Если интеграл:
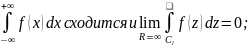
 (5.14)
(5.14)
В формуле (5.14) вычеты берутся по всем особым точкам функции f(z) лежат в верхних полюсах.
3)
Интеграл вида: Im= R(x)dx
(5.15) R(x)-рациональная
функция. При вычислении интеграла (5.15)
используется следующая лемма:
R(x)dx
(5.15) R(x)-рациональная
функция. При вычислении интеграла (5.15)
используется следующая лемма:
Лемма (5.4): Шварца:
Пусть α>0 и выполняются следующие условия:
1)Функция
g(z)
неприрывна в области Im
z≥0
при |z|≥
2)M(R)=max(g(z))/→0
при R→∞,
где
 |z|=R,
Im
z≥0,
тогда
|z|=R,
Im
z≥0,
тогда
 Интеграл (5.15) сходится в тот и только в
том случае, когда на действительной оси
нет полюсов функции R(z)
и кроме того
Интеграл (5.15) сходится в тот и только в
том случае, когда на действительной оси
нет полюсов функции R(z)
и кроме того

Замечание:
Если функция R(x)-действительна,
xϵR,
α>0,
то выделим действительную и мнимую
часть:
 (5.16) получим:
(5.16) получим:


Аналитическое продолжение:
П(6.1)Определение и основные свойства:
Определение: Пусть выполняются следующие условия:
1)Функция f(z) определена на множестве E;
2)Функция F(z)- регулярна в области Д содержится множество Е;
3)F(z)=f(z), zϵE, тогда F(z) называется аналитическим продолжением f(z) с множества Е в область Д. Самым важным свойством аналитического продолжения является его единственность.
Т(6.1)Принцип аналитического продолжения.
Пусть множество Е имеет предельную точку а принадлежащую области Д , тогда аналитическое продолжение с множества Е в область Д единственно.
Доказательство:
Допустим,
что у функции f(z)
определена на Е имеется 2 аналитических
продолжения:
 в области Д т.к.
в области Д т.к.
 при zϵE,
то по теореме единственности:
,
zϵD.
при zϵE,
то по теореме единственности:
,
zϵD.
Т(6.2) Единственности.
Пусть
функция f(z)регулярна
в области D
и f(z)=0
(n=1,2,3,…,n),
тогда { послед-ть
послед-ть
 ;
;
 тогда f(z)=0
в области D;
тогда f(z)=0
в области D;
1)Пусть
функция f(z)регулярна
в области D
и f(z)=0
на множестве
 которое содержится в Е.
которое содержится в Е.
2)Пусть
f(z)
и g(z)
регулярна в области Д и совпадает на
множестве, которое содержит в области
Д и имеет предельную точку тогда f(z) g(z)
в области D.
g(z)
в области D.
В частности Е кривая в Д или подобласть в Д, то существует не более одного аналитического продолжения в области Д.
П(6.2) Аналитическое продолжение e(экспонента тригонометрическая и гиперболическая).
 sin
z,
cos
z,-
эти функции аналитически
продолжаются функцией
sin
z,
cos
z,-
эти функции аналитически
продолжаются функцией
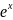 , sinz,
cosz.
Положим, что
=
, sinz,
cosz.
Положим, что
= Ряд сходится при всех следовательно
сумма регулярна при всех . При действительных
z=x
следует
Ряд сходится при всех следовательно
сумма регулярна при всех . При действительных
z=x
следует
 По теореме об аналитических продолжениях
она является аналитическим продолжением
По теореме об аналитических продолжениях
она является аналитическим продолжением

Т(6.3) Пусть f(z) и g(z)-целые функций, следовательно, f(z) ± g(z), f(z)·g(z), f( g(z))- целые.
Доказательство следует из свойств регулярных функций. Определённая функция sinz, cosz, sh z, chz, как суммы рядов:

Т.к. эти
ряды сходятся при любом z,
то sinz,
cosz,
chz,
shz
-целые функции. Эти функции аналитические
продолжения. Функции tgz,
ctgz,
cthz,thz,
введём: tgz= ctgz=
ctgz= thz=
thz= cthz=
cthz= tgz-регулярна
z≠∞,
z≠
tgz-регулярна
z≠∞,
z≠ ctgz-регулярна
z≠kπ,
thz=регулярна
z≠i(
ctgz-регулярна
z≠kπ,
thz=регулярна
z≠i( ;
cthz
– регулярна z≠i
;
cthz
– регулярна z≠i .
Все эти функции выполняются для
комплексного z.
.
Все эти функции выполняются для
комплексного z.
Пример
(1): Покажем, что
 (6.1)
При
(6.1)
При
 – равенство выполняется, фиксируя
– равенство выполняется, фиксируя
 ,
Левая и правая часть из
,
Левая и правая часть из
 они совпадают при
они совпадают при
 ;
Значит, по следствию (2) из Т(6.2) они
совпадают при всех
;
Значит, по следствию (2) из Т(6.2) они
совпадают при всех
 .
Теперь пусть
.
Теперь пусть
 Следует: Левая и правая часть (6.1) –
являются целыми от функции
и совпадают при
следовательно
Следует: Левая и правая часть (6.1) –
являются целыми от функции
и совпадают при
следовательно

Конформное отображение
