Билет № 8. Замена переменных в двойном интеграле. Двойной интеграл в полярной системе координат. Примеры.

Пусть функции х=φ(U,V) и у=ψ(U,V) (1)

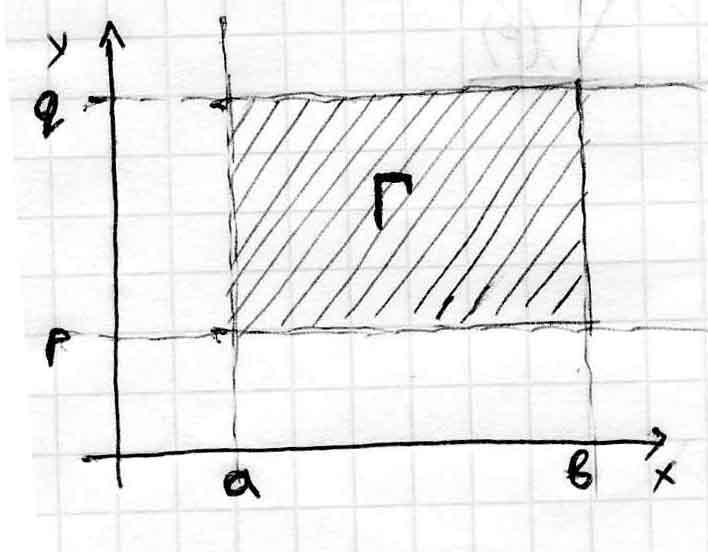
–функции,осуществляющие взаимно однозначное непрерывное дифференцируемое отображение области Γ плоскости О'UV на область G плоскости Оху. Это означает,что существует обратное непрерывное дифференцируемое отображение U=η(x,y) и V=χ(х,у) области G на область Г и в области Г отличен якобиан преобразования, т.е.

|δφ/δU δφ/δV |

I(U,V)= |δψ/δU δψ/δV | ≠ 0, (U,V) принадлежит Г.

Величины U и V можно рассматривать как прямоугольные координаты для точки области Г и в то же время как криволинейные координаты точек области G.

Если в двойном интеграле _(Р)∫∫f(x,y)dxdy произвести замену переменных по G по формулам (1), то областью интегрирования полученного интеграла будет уже область Г, которая при надлежащем выборе функций φ(U,V) и ψ(U,V) может оказатся значительно проще области G, и имеет место формула _G∫∫f(x,y)dxdy=_Г∫∫f(φ(U,V), ψ(U,V))dUdV.

Пример.

Вычислить интеграл _G∫∫ корень(ху)dxdy, если область G ограничена кривыми

y²=ах xy=p (0<a<b, 0<p<q)

y²=bх xy=q

Перейдём к новым переменным U и V по формулам y²=Ux, xy=V

x=U ^-1/2V ^2/3 y= U^1/3V ^1/3

δх/δU= -1/3 U ^-4/3V ^2/3 δх/δV= 2/3 U ^-1/3V ^-1/3

δy/δU= 1/3 U ^-2/3V ^1/3 δх/δV= 1/3 U ^1/3V ^-2/3

|-1/3 U ^-4/3V ^2/3 2/3 U ^-1/3V ^-1/3 |

I(U,V)= |1/3 U ^-2/3V ^1/3 1/3 U ^1/3V ^-2/3 | = -1/3U , при U>0

_G∫∫ корень(ху)dxdy – 1/3_Г∫∫ корень(V) dU dV/U= 1/3 _a^b∫ dU/U _p^q∫ корень(V)dV=1/3lnU_a^b| 2/3 V^2/3 _p^q| = 2/9(q ^3/2 - p^3/2)ln b/a

x=r cosφ y=r sinφ

|cosφ -r sinφ |

I(U,V)= |sinφ r cosφ | =r

_G∫∫ f(х,у)dxdy= _Г∫∫ f(r cosφ, r sinφ)drdφ.

Билет № 9. Применение двойного интеграла к вычислению площади плоской области, объёма, площади поверхности. Примеры.

Косяк……………………………………………………………………………………

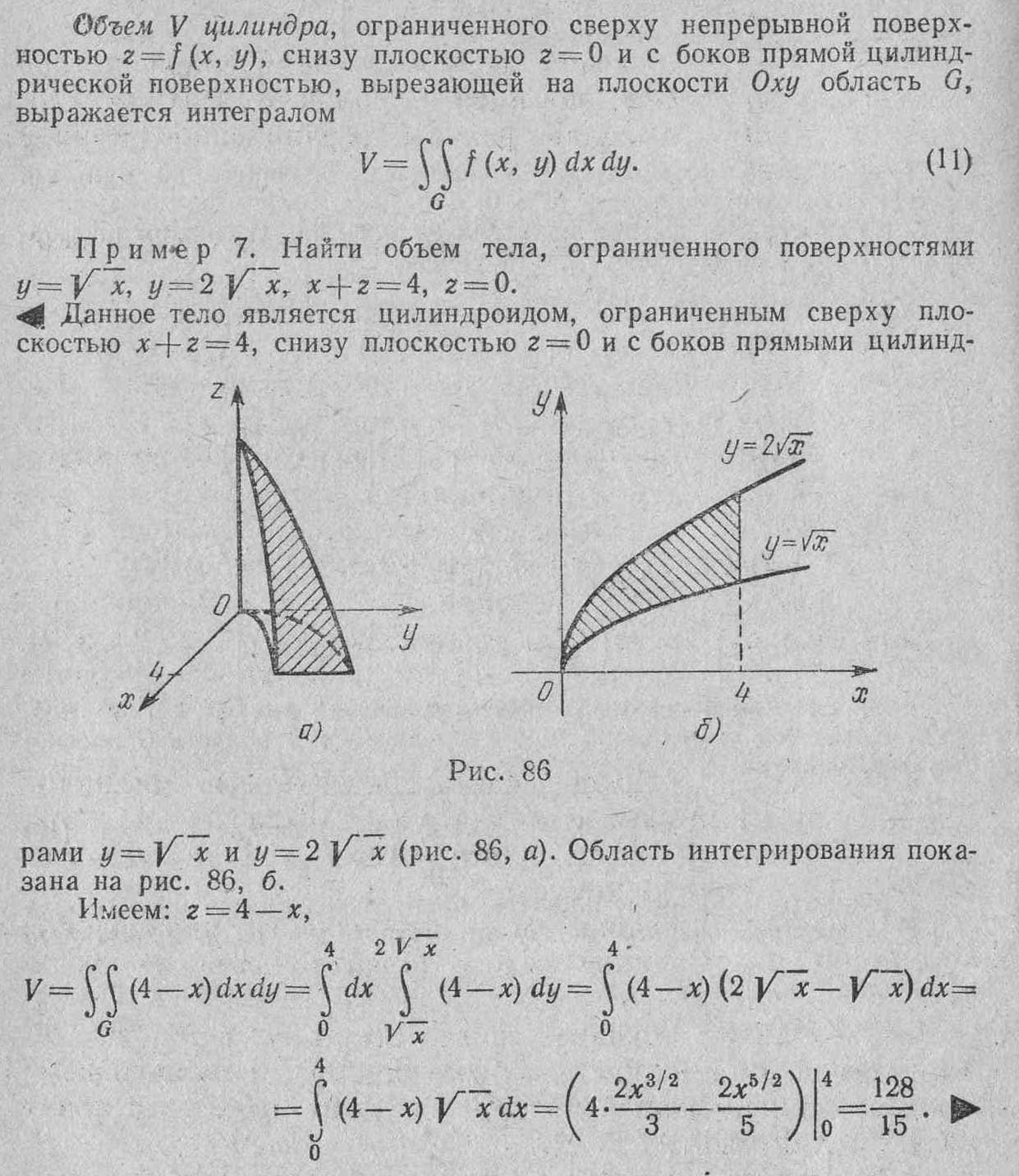
Билет № 10. Применение двойного интеграла в механике. Примеры.

Если пластинка занимает область G плоскости Оху и имеет переменную поверхностную плотность γ=γ(x,y), то масса М пластинки и её статические моменты М_х и М_у относительно осей Ох и Оу выражается двойным интегралом М=_G∫∫γ(x,y)dxdy, М_х=_G∫∫ уγ(x,y)dxdy, М_у=_G∫∫ хγ(x,y)dxdy.

Координаты центра масс х и у пластинки определяются следующим образом

(здесь и далее там где нижнее подчеркивание , на самом деле верхнее подчеркивание,потому так легче шпору делать )

х = М_у/М = _G∫∫ хγ(x,y)dxdy/ _G∫∫γ(x,y)dxdy

у = М_х/М = _G∫∫ уγ(x,y)dxdy/ _G∫∫γ(x,y)dxdy

Моменты инерции пластинки относительно осей Ох и Оу соответственно равны.

I_x= _G∫∫ у²γ(x,y)dxdy

I_y= _G∫∫ x²γ(x,y)dxdy

А моменты инерции относительно начала координат (полярный момент инерции) равен

I₀= _G∫∫ (х² + у²)γ(x,y)dxdy= I_x + I_y

Если пластинка однородна и плотность её не указана, условимся считать γ(x,y)=1

Пример.

Найти координаты центра масс однородной пластинки, ограниченной кривыми у=х², х+у=2а (а >0)

Линии пересекаются в точках М₁ (-2а, 4а) и М₂ (а, а) =>

S= _G∫∫dxdy=_2а ^а∫dx _х^2/а ^2a-x∫dy = _-2а ^а∫(2a - x - x²/a)dx = (2ax – x²/2 – x³/3a) |_-2a ^a = 9/2 a²

М_х= _G∫∫ydxdy=_-2а ^а∫dx _х^2/а ^2a-x∫ydy= 1/2 -_2а ^а∫((2a-x)²-x⁴/a²)dx= 1/2(-(2a-3)³/3 – x⁵/5a)|_-2a^a =36/5a⁵

М_y= _G∫∫ydxdy=_-2а ^а∫xdx _х^2/а ^2a-x∫dy= -_2а ^а∫(x(2a-x-x²/a)dx= (ax² – x³/3 –x⁴/4a)|_-2a^a=-9/4 a²

x = М_y/S = -a/2 y = М_y/S=8/5 a