Б илет № 7. Двойной интеграл и его свойства. Вычисление двойного интеграла в декартовых координатах.

Рассмотрим тело (V), которое сверху ограничено поверхностью z=f(x,y), с боков цилиндрической поверхностью с образующими, параллельными Оz, и снизу плоской фигурой (Р) на плоскости Oxy. Требуется найти объем этого тела. Разложим (Р) сетью кривых на части (Р₁), (Р₂),…, (Р_n) и рассмотрим ряд цилиндрических столбцов, которые имеют свои основания и в совокупности составляют данное тело.

d²z=(δ²z/δx² )d²x + (δ²z/δx δy )dxdy + (δ²z/δy² ) d²y

U=xy + yz + zx

d²U= (δ²φ/δx² ) + (δ²φ/δy² ) +(δ²φ/δz² ) + (δ²φ/δxδy )dxdy + (δ²φ/δyδz )dydz + (δ²φ/δxδz )dxdz

δU/δx = y + x

δU/δy = x + z

δU/δz = y + x

δ²U/δx²=0 (δ²U/δx δy )=1

δ²U/δy²=0 (δ²U/δy δz )=-1

δ²U/δz²=0 (δ²U/δx δz )=1

В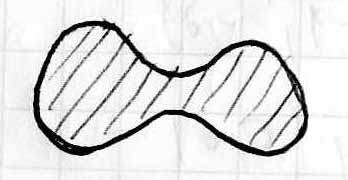 каждой фигуре (Р_i) возьмем произвольно по точкам (ξ_i, η_i). Если приближенно принять каждый столбец за настоящий цилиндр с высотой равной аппликате f(ξ_i, η_i), то объём отдельного столбца оказывается приближенно равным f(ξ_i, η_i) Р_i, где Р_i – площадь фигуры (Р_i). В таком случае V≈ ⁿ_i=1Σ f(ξ_i, η_i) Р_i

Для уточнения этого равенства будем уменьшать (Р_i), увеличивая их число. В пределе при D(Р_i)→ 0. Это равенство делается точным так, что V= lim ⁿ_i=1Σ f(ξ_i, η_i) Р_i (*)

Здесь D(P_i) обозначает диаметр точечного множества, т.е. точную верхнюю границу расстояний между двумя произвольными точками множества. Предел этого вида и есть двойной интеграл от функции f(x,y) по множеству P_i. Он обозначается символом _(Р)∫∫f(x,y)dP. Т.о. V=_(Р)∫∫f(x,y)dP.

σ= ⁿ_i=1Σ f(ξ_i, η_i) Р_i

λ- наименьший из диаметров частичной подобласти

Опр. Конечный предел I интегральной суммы σ при λ→0 называется двойным интегралом функции f(x,y) в области и обозначается символом I=_(Р)∫∫f(x,y)dP.

Функция имеющая интеграл называется интегрируемой.

Теорема

Всякая непрерывная в области (P_i) f(x,y) интегрируема.

Основные свойства двойного интеграла.

1. Двойной интеграл от суммы конечного числа функция равен сумме двойных интегралов от слагаемых функций.

2. Постоянный множитель подынтегральной функции можно вынести за символ двойного интеграла.

3. Если область интегрирования (Р) разбита на 2 части (Р*) и (Р**), то интеграл

_(Р)∫∫f(x,y)dP=_(Р*)∫∫f(x,y)dP + _(Р**)∫∫f(x,y)dP.

4. Если во всех точках области (Р) функции φ(х,у) и f(x,y) удовлетворяет условию f(x,y) ≥ φ(х,у), то _(Р)∫∫f(x,y)dP ≥ _(Р)∫∫φ(x,y)dP.

5. Если f(х,y) во всех точках области (Р) удовлетворяет неравенствам m ≤ f(x,y) ≤ M, то m ≤ _(Р)∫∫f(x,y)dP ≤ M, где Р – площадь области (Р).

6. Двойной интеграл равен произведению значений подынтегральной функции в некоторой точке области интегрирования на площадь этой области, т.е. _(Р)∫∫f(x,y)dP= f(ξ, η) Р (**)

Значение f(ξ, η) Р определяется из (**) и называется средним значением функции f(x,y) в области (Р)

Если f(x,y) ≡1, то => _(Р)∫∫dP=Р ≤MP

В самом деле в этом случае двойной интеграл выражает оббьем прямого цилиндра с высотой 1.

Вычисление двойного интеграла.

П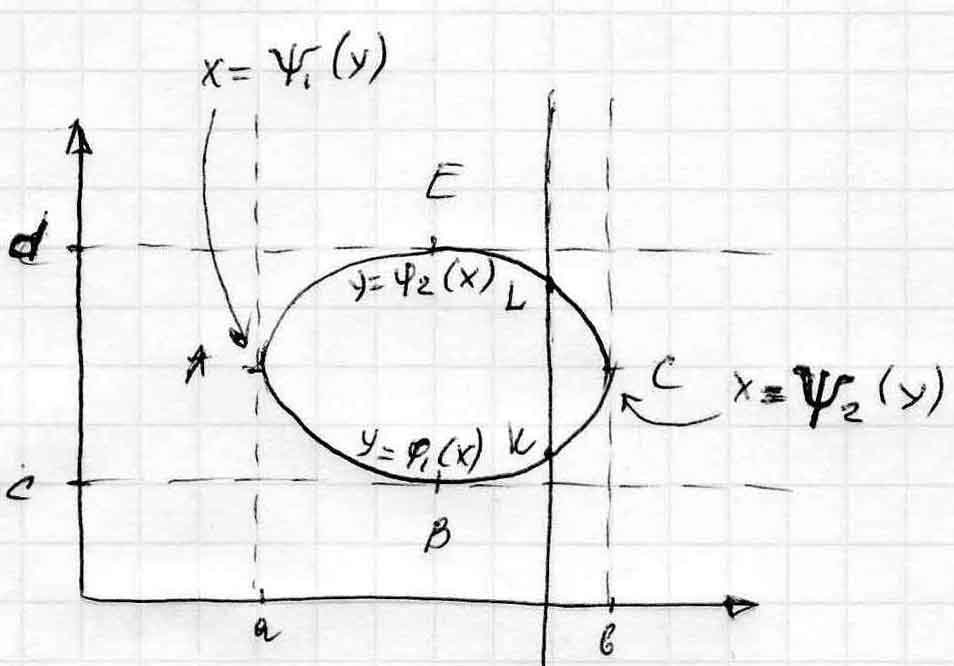 ри вычислении двойного интеграла _(Р)∫∫f(x,y)dP элемент площади dP удобно представить в другом виде. Будем разбивать (Р) на частичные подобласти системы линий х=con∫t, y=con∫t. Частичными подобластями в этом случае будет прямоуглоьник со сторонами параллельными осям координат. А элемент d(P) запишется в виде dP=dxdy. Т.е. элемнт площади в прямоугольных координатах является произведением дифференциалов независимых переменных.

_(Р)∫∫f(x,y)dP=_(Р)∫∫f(x,y)dxdy (1)

При вычислении (1) будем опираться на тот факт, что выражение представляет собой объём V цилиндрического тела с основанием (Р), ограниченного поверхностью z=f(x,y), а также на ранее полученную формулу объёма тела с заданным поперечным сечением.

V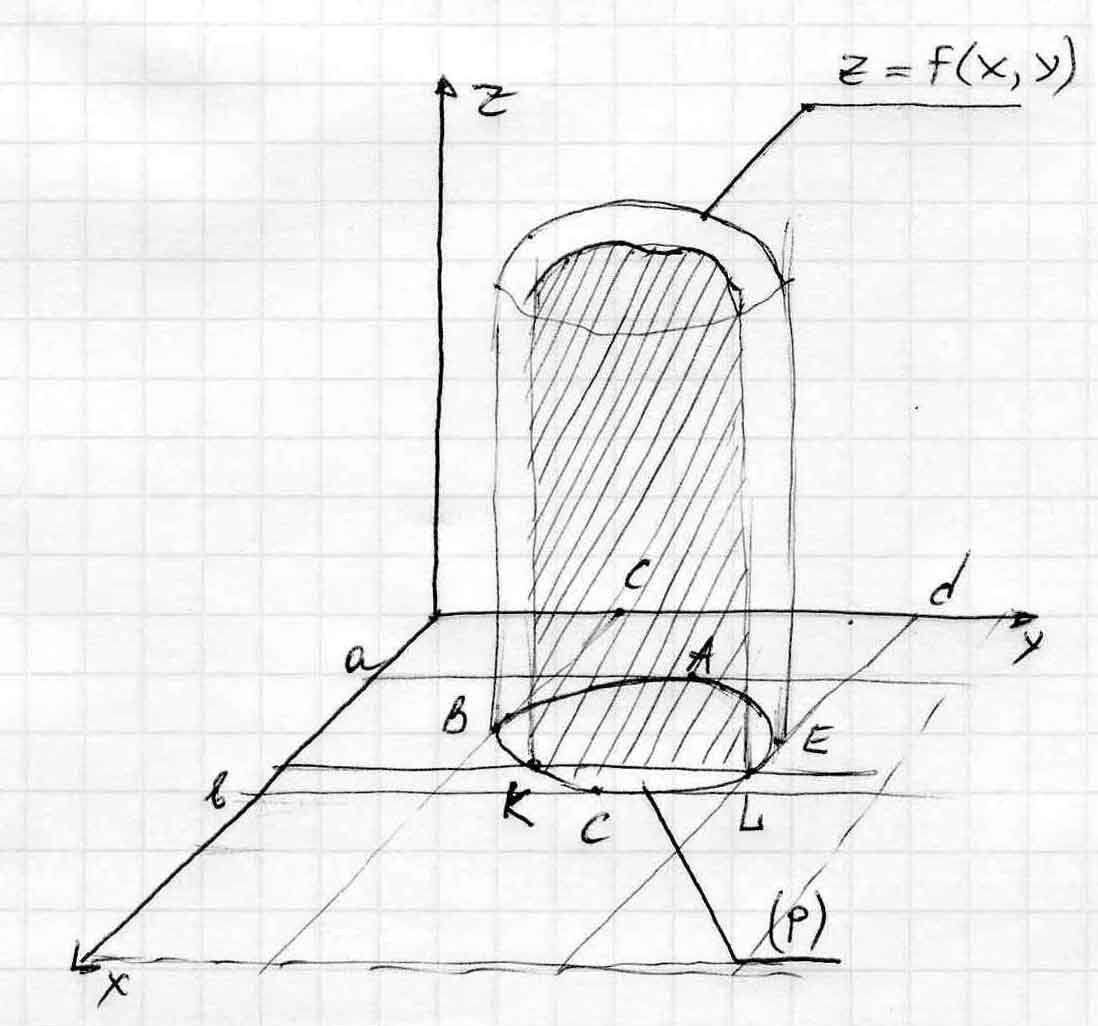 =^a_b∫ S(x)dx (2), где S(x) – площадь поперечного сечения тела плоскостью перпендикулярной Ox, а x=а, х=b - уравнения плоскостей, ограничивающих данное тело.

Предположим, что (Р) удовлетворяет условию:

1. Любая прямая, параллельная Ох или Оу пересекает границу области не более чем в двух точках.

2. Область Р заключим внутри прямоугольника a ≤ x ≤ b,

c ≤ y ≤ d

Обозначим через А,В,С и Е точки касания прямоугольника и (Р).

Точками А и С границы разбиваются на 2 линии – АВС и АЕС, каждая из которых пересекается с любой прямой параллельной Оу в одной точке. Поэтому их уравнения можно записать в форме, разрешенной относительно у:

у=φ₁(х) (АВС)

у=φ₂(х) (АЕС), где φ₁(х) и φ₂(х) функции однозначные на отрезке АВ. Аналогично точками В и Е граница разбивается на линии (ВАЕ) и (ВСЕ), уравнения которых можно записать так

х=ψ₁(у) (АВЕ)

х= ψ₂(у) (ВСЕ), где ψ₁(у) и ψ₂(у) функции однозначные в отрезке СD.

Рассечем рассмотренное тело произвольной плоскостью, параллельной плоскости Оyz, т.е. x=con∫t, x принадлежит [a,b]. В сечении получим криволинейную трапецию KLMN, площадь которой выражается обыкновенным интегралом от функции f(x,y), рассматриваемой как функция одной переменной у, причем у измеряется от ординаты точки K до ординаты точки L, т.к. уравнение линий (АВС) есть у=φ₁(х),а линии (АЕС) есть у=φ₂(х), то эти ординаты при взятом х соответственно равны у=φ₁(х) и у=φ₂(х) => _φ1(х) ^φ2(х)∫ f(x,y)dy даёт выражение площади криволинейной трапеции KLMN. Величина этого интеграла зависит от выбранного значения x.

Другими словами, площадь рассматриваемого поперечного сечения является некоторая функция от х. мы обозначим её как S(x)= _φ1(х) ^φ2(х)∫ f(x,y)dy (3)

Согласно формуле (2) объём всего тела будет равен ^a_b∫ S(x) заменим в (2) S(x) выражением (3). Окончательно получим: _(Р)∫∫f(x,y)dxdy = _a^b∫[_φ1(х) ^φ2(х)∫ f(x,y)dy] dx или V = _a^b∫ dx _φ1(х) ^φ2(х)∫ f(x,y)dy

Пределы внутреннего интеграла переменны, они указывают границы изменения у при x=con∫t. Пределы внешнего интеграла постоянны, они указывают границы изменения аргумента х. Меняя роли х и у, то есть рассматривая сечение тела плоскостями y=con∫t, причём с≤ y≤ d, мы найдем сначала, площадь Q(y) такого сечения равна _ψ1(х)^ψ2(х)∫ f(x,y)dх, где у при интеграле считается величиной постоянной. Интегрируя затем Q(y) в пределах изменения у, то есть от с до d, мы придем ко второму выражению для двойного интеграла _(Р)∫∫f(x,y)dxdy= _c^d∫[_ψ1(х) ^ψ2(х)∫ f(x,y)dx] dy (5)

З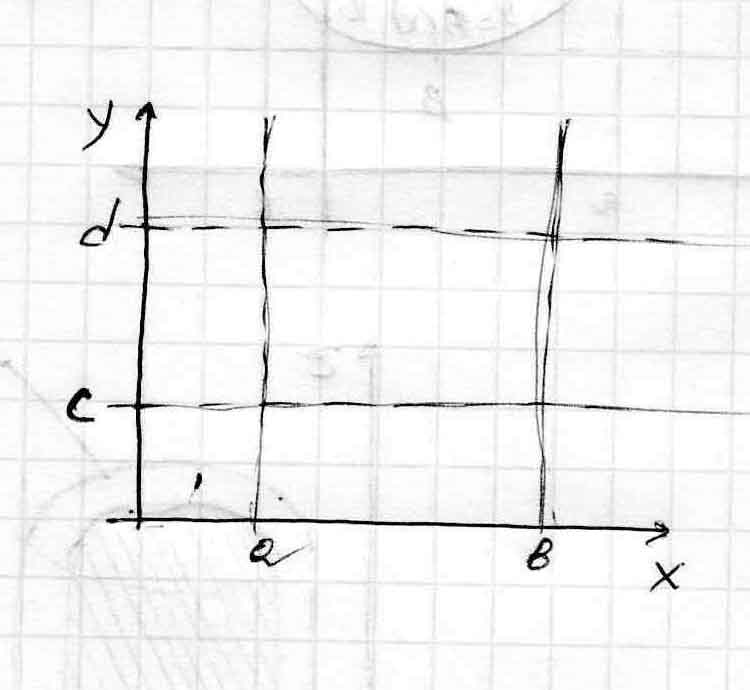 десь интегрирование совершается сначала по х, а потом по у. Выражения стоящие в правых частях формул (4) и (5) называются двукратными интегралами от функции f(x,y) по (Р).

Формулы привидения двойного интеграла к двукратному имеют простой вид, когда (Р) является прямоугольником со сторонами, параллельными осям координат.

_(Р)∫∫f(x,y)dxdy = _a^b∫[_φ1(х) ^φ2(х)∫ f(x,y)dy] dx= _c^d∫[_ψ1(х) ^ψ2(х)∫ f(x,y)dx] dy

В других случаях для сведения двойного интеграла к двукратному необходимо :

1. Построить область интегрирования

2. Установить порядок интегрирования, т.е. наметить по какой переменной будет произведено внутреннее интегрирование, а по какой внешнее.

3. Поставить переделы интегрирования.