Билет 1.

Множества. Основные определения. Декартово произведение множеств.

Множество – совокупность различных предметов//объектов одной природы, рассматриваемых как единое целое. Мощность – число элементов. |A|

Способы задания

1) перечислить все элементы

2) определить принадлежность

3) задать процедуру множества

если элементы мн. А мн. В, то А В(подмножество)

А В (собственное подмножество), если А В, но А≠В

Несобственными подможествами А являются Ø и А.

Универсальное множество Е – такое, что все рассматриваемые в данном классе задач множества являются его подмножествами.

В общем случае мн-вом может являться совокупность таких объектов, нек. из которых сами являются мн-вами. Тогда говорят о системе множеств. система множеств В(М) называется булеаном мн-ва М, если она состоит из подмножества мно-ва М, включая само М и Ø.

например М={a,b,c}

B(M)={a; b; c; a,b; a,c; b,c; a,b,c; Ø }

|M|=3. |B(M)|=2^|M|=8

Мн-ва равномощные мн-ву N называется счётными.

Мн-ва равномощные мн-ву действ. чисел наз-ся континуальными.

Совокупность упорядоченных по опр. признаку мн-в называется картежом.

А={а₁, а₂…а_n}

B={b₁..b_m}

Декартово произведение множеств (АхВ) будет множество всех возможных упорядоченных пар. АхВ≠ВхА

Кол-во элементов дек. произведения (мощность) равна произведению мощностей этих мн-в. На практике часто рассм. произведение мн-ва само на себя.

Билет 2

Основные операции на множествах, свойства операций над множествами.

Операции:

-бинарные

объединение С=А B. сост. из всех эл-тов, принадлежащих хотя бы одному из мн-в

пересечение С=А B. сост. из всех эл-тов, принадлежащих обоим мн-вам

дополнение до универсального , если А+ =Е, А* = Ø

разность А\В=А* =С. сост из элементов А, исключая элементы В.

симметрическая разность АΔВ=С=(А\В)+(В\А)= (А* )+( *В)

Свойства

- коммутативность

А+В=B+A

A*B=B*A

-ассоциативность

(A+B)+C=A+(B+C)

(A*B)*C=A*(B*C)

-дистрибутивность

A*(B+C)=A*B+А*C

A+B*C=(A+B)*(А+C)

-тождественность

А+А+..+А=А

А*А*..*А=А

-поглощение

А+(А*В)=А

-инволюция

-правило Де Моргана

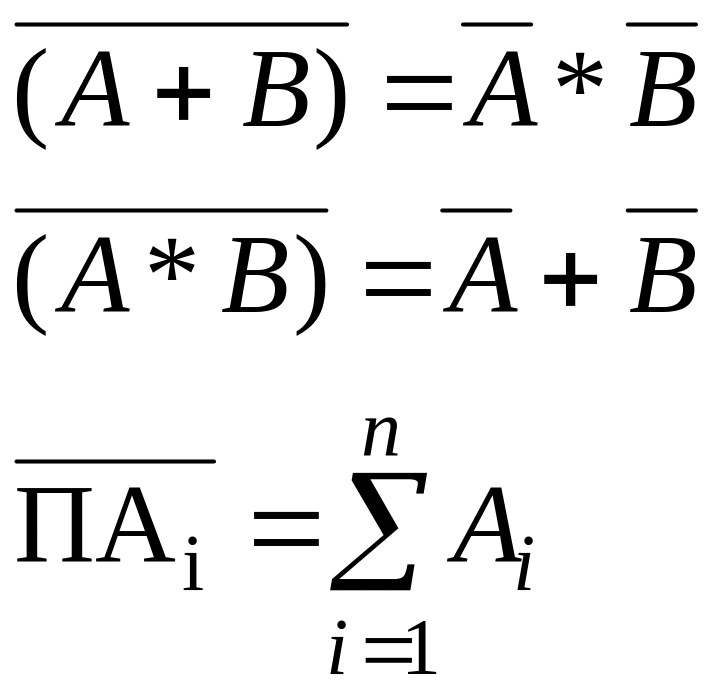
-склеивание

Общие:

А+Е=Е А* Ø= Ø

А*Е=А = Ø

А+ Ø=А А+ =Е

А* = Ø

Билет 3.

Отношения. Бинарные отношения и их свойства.

При рассм. св-в отдельных эл-тов неск. мн-в или одного, используется понятие отношения.

При рассм. св-в эл-тов одного множества ис-ся одноместное (унарное) отношение

при рассм. пар элементов одного или разл. мн-в говорят о двумерных (бинарных отношениях)

Из всего мн-ва возможных эл-тов отн. R выделяют то подмножество, кот. обладает данным св-вом.

Свойства бинарных отношений.

-Отношение R рефлексивно, если для х Х находится в отношении R с самим собой.

Если выполняется не для всех х, то нерефлексивное, если не выполняется ни для одного х, то антирефлексивное. Пример- отношение равенства.

-Отношение R симметричное, если для пары эл-тов (а,b) Х выполнение aRb влечет выполнение bRa_. Пример – отношение эквивалентности

- Отношение R транзитивное, если для всех элементов x,y,z Х. Выполнение xRy, yRz влечет, что xRz.

Отношение эквивалентности – обладает всеми тремя.

Бинарным отношением R называется отношенем не строгого порядка, если оно рефлексивно, антисимметрично(аRb=> a=b), транзитивно. Строгого порядка, если оно антирефлексивно, антисимметрично, транзитивно.