НИЖЕГОРОДСКИЙ ГОСУДАРСТВЕННЫЙ УНИВЕРСИТЕТ

им. Н.И. ЛОБАЧЕВСКОГО

В.А. Рябинин

Транспортные задачи линейного программирования

Лабораторная работа №5

Нижний Новгород

2005

1. Содержательное описание

Из крупнейших месторождений России:

Медвежье(170 млн. м³/сутки), Уренгой (160 млн. м³/сутки) и Янбург(120 млн. м³/сутки). Для сокращения, обозначены соответственно буквами: М1, М2, М3.

Поступает газ в Германию (150 млн. м³/сутки); Австрию(90 млн. м³/сутки); Венгрию(70 млн. м³/сутки) и Польшу(140 млн. м³/сутки). Для сокращения, обозначены соответственно буквами: S1, S2, S3, S4.

Стоимость передачи газа за сутки (у.е/млн. м³) из месторождений к потребителям.

Добыча Продажа _		М1	М2	М3
		170	160	120
S1	150	5	3	3
S2	90	3	4	5
S3	70	2	2	3
S4	140	4	2	3

Необходимо передать газ потребителям с наименьшими затратами.

2. Формализация.

Пусть x_ij- количество газа, поставляемое в страну Si из месторождения Mj. a_i – норма газа, поступающая стране Si, b_j- количество добываемого газа на месторождении Mj.

Тогда для того чтобы поставки газа были выполнены необходимо:

1) Σ_j x_ij =a_i, i=1..4; j=1..3

2) Σ_i x_ij =b_j, i=1..4; j=1..3

x_ij≥0 (Поставки должны быть положительными)

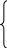
x₁₁+x₁₂+x₁₃=150

x₂₁+x₂₂+x₂₃=90 (U)

x₃₁+x₃₂+x₃₃=70

x₄₁+x₄₂+x₄₃=140

x₁₁+x₂₁+x₃₁+x₄₁=170

x₁₂+x₂₂+x₃₂+x₄₂=160 (V)

x₁₃+x₂₃+x₃₃+x₄₃=120

x_ij≥0 i=1..4; j=1..3

Представим данные в виде таблицы:

Продажа _		М1	М2	М3
		170	160	120
S1	150	5x11	3x12	3x13
S2	90	3x21	4x22	5x23
S3	70	2x31	2x32	3x33
S4	140	4x41	2x42	3x43

Добыча

В левых верхних углах ячеек указаны стоимости транспортировки газа в страну i из месторождения j:

5	3	3
3	4	5
2	2	3
4	2	3

C_ij=

А значит условие минимальности затрат на транспортировку можно записать так:

F= Σ_iΣ_j c_ij*x_ij→min

или

F=5*x₁₁+3*x₁₂+3*x₁₃+3*x₂₁+4*x₂₂+5*x₂₃+2*x₃₁+2*x₃₂+3*x₃₃+4*x₄₁+2*x₄₂+3*x₄₃→min

3. Двойственная задача.

Нам надо оценить выгодность передачи газа через ту или иную трубу. Для этого оценим потенциалы стран U_i и потенциалы месторождений V_j. Так как цель- минимизировать затраты на транспортировку, то сумма потенциалов не должна превышать затрат:

U_i+V_j≤C_ij, при x_ij=0

U_i+V_j=C_ij, при x_ij>0

x_ij≥0 i=1..4; j=1..3

U₁+V₁≤5

U₁+V₂≤3

U₁+V₃≤3

U₂+V₁≤3

U₂+V₂≤4

U₂+V₃≤5

U₃+V₁≤2

U₃+V₂≤2

U₃+V₃≤3

U₄+V₁≤4

U₄+V₂≤2

U₄+V₃≤3

T=150*U₁+90*U₂+70*U₃+140*U₄+170*V₁+160*V₂+120*V₃→max