Двоичный-симметричный канал

Двоичным-симметричным каналом называется канал, в котором в любом символе с вероятностью происходит ошибка типа замещения , причем замещения различных символов статистически независимы . В этом случае произвольное слово Х преобразуется замещением символов в любом слове Y c вероятностью , так что . Поэтому все ошибки в двоичном канале исправить невозможно . Обозначим через математическое ожидание вероятности исправления ошибок в слове кода

при декодировании D в предположении , что все кодовые слова равновероятны. Очевидно , что

.

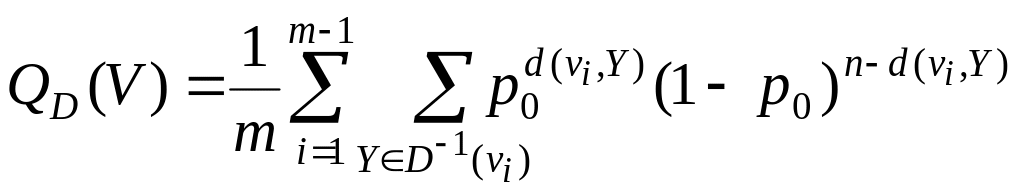Величина называется достоверностью декодирования D при коде V.

Заметим, что в силу условия 0 < функция возрастает при уменьшении d(X,Y) . Поэтому максимальную достоверность имеет такое декодирование D , при котором каждое слово отображается в ближайшее к нему кодовое слово .

Достоверность такого декодирования D будем просто называть достоверностью кода и обозначать через Q(V) , а разбиение множества на окрестности будем называть в этом случае разбиением на окрестности максимальной достоверности .

Приведем в качестве примера таблицу, в которой для кода дается одно из разбиений на окрестности максимальной достоверности и подсчитана достоверность кода .

0011 0000 0001 0010	0111 0101 0100 0110	1011 1001 1010 1101 1000	1110 1100 1111

.

Канал , в котором в каждом слове длины n может произойти любая ошибка заданного типа кратности не более s

Код будем называть кодом с исправлением ошибок заданного типа , если существует декодирование , при котором в каждом кодовом слове исправляются все ошибки рассматриваемого типа кратности не более s .

Код является кодом с исправлением s ошибок заданного типа только тогда , когда множества , попарно не пересекаются .

Заметим ,что в случае ошибок типа замещения множество З(Х) совпадает с метрической окрестностью радиуса s в слове Х .

Метрической окрестностью радиуса s точки Х называется множество точек , удаленных от Х на расстояние более s .

Поэтому условие непересечения множеств , равносильно тому , что кодовое расстояние d(V)>2s .

Аналогичное метрическое описание допускает коды с исправлением фиксированного числа ошибок других типов .

Тип назовем симметричным , если он является объединением некоторых из множеств .

Для ошибок симметричного типа определим из пары двоичных слов из функцию как наименьшее число одиночных ошибок типа преобразующее X в Y , или как , если слово Х нельзя преобразовать в слово Y ошибками типа .

Кодовым расстоянием кода в метрике будем называть величину . В этом случае условие непересечения множеств также равносильно тому , что d(V)>2s и , следовательно код является кодом с исправлением ошибок типа тогда и только тогда , когда d(V)>2s .

Заметим , что метрика Хемминга совпадает с метрикой при .

Пример. Сравним расстояние между словами Х = 00000 и Y = 01101 , а также между словами Y = 01101 и Z = 11010 в метрике Хемминга и в метрике , где .

Имеем d(X,Y)=3 , d(Y,Z)=4 , а соответственно и .

Для ошибок типа , состоящего из выпадений , вставок и замещений , но не являющихся симметричными , функцию определим на парах двоичных слов из следующим образом :

= 2 ,

где - минимальное число одиночных ошибок типа , преобразующих слово X в Z , или , если слово Х нельзя преобразовать в слово Z ошибками типа .

И в условиях этой метрики можно также сказать , что код является кодом с исправлением s ошибок типа тогда , когда для любых и имеет место d( )>2s .

В случае будем иметь :

.

Заключение. Наряду с задачами исправления ошибок можно рассматривать задачи обнаружения ошибок. Очевидно, что при использовании кода V обнаружить лишь те ошибки, которые преобразуют кодовые слова в кодовые слова. Отсюда, в частности, следует, что код V c кодовым расстоянием d всегда позволяет обнаружить d-1 или менее одиночных ошибок типа замещения.