
- •Дискретная математика
- •Реализация функций формулами
- •Важнейшие замкнутые классы
- •Этот класс содержит ровно булевых функций , зависящих от переменных .
- •Этот класс также содержит ровно булевых функций , зависящих от переменных и замкнут . Функция называется двойственной для функции .
- •Алгоритмы построения минимальных дизъюнктивных нормальных форм Совершенная дизъюнктивная нормальная форма (д.Н.Ф.)
- •Способы построения тупиковых д.Н.Ф.
- •Критерий поглощения.
- •Локальные алгоритмы упрощения д.Н.Ф.
- •Необходимое и достаточное условие вхождение конъюнкции в
- •Пусть и .
- •Двоичный-симметричный канал
- •Канал , в котором в каждом слове длины n может произойти любая ошибка заданного типа кратности не более s
- •Примеры кодов с исправлением одиночных ошибок различных типов.
- •Очевидно , что число w(X) равно сумме номеров единичных символов слова х.
- •Элементы теории графов
- •Задача о кратчайшем пути
- •Нахождение кратчайшего пути в графе с ребрами единичной длины
- •Нахождение кратчайшего пути на графе с ребрами произвольной длины
- •Задачи, решаемые методами теории потоков
- •Основные понятия и определения теории потоков Конечный граф (х,т) без петель называется сетью , если каждой дуге
- •В любой сети максимальное значение суммарного потока на конечных дугах равно минимальной пропускной способности разреза.
- •Определение максимального потока методом разметки вершин
- •Последовательность решения примера
- •Транспортная задача по критерию стоимости
МИНИСТЕРСТВО ОБРАЗОВАНИЯ РОССИЙСКОЙ ФЕДЕРАЦИИ
РОСТОВСКИЙ ГОСУДАРСТВЕННЫЙ СТРОИТЕЛЬНЫЙ УНИВЕРСИТЕТ
|
Утверждена на заседании кафедры ИСС 29 сентября 1999 г. |
Методические указания
"Дискретная математика"
для студентов дневной формы обучения
специальности ИСС
Ростов-на-Дону
2000
УДК 519.6 (075.В)
Методические указания "Дискретная математика" для студентов дневной формы обучения специальности ИСС. – Ростов – н/Д: Рост. гос. строит. ун-т, 2000.- 40 c.
Изложен теоретический материал по лингвистическим основам информатики.
Предназначена для студентов дневной формы обучения специальности ИСС.
Составитель:
канд. физ.-мат. наук, доц. А.Е. Богданов
Рецензент:
д-р физ.-мат. наук, проф. М.Г. Селезнев
Редактор Т.М. Климчук
Темплан 2000 г., поз. 105
ЛР 020818 от 13.01.99. Подписано в печать . . 2000. Формат 60х84/16.
Бумага белая. Ризограф. Уч. – изд. л. 2,0. Тираж 100 экз. Заказ
Редакционно-издательский центр
Ростовского государственного строительного университета
344022, Ростов н/Д, ул. Социалистическая, 162
РОСТОВСКИЙ ГОСУДАРСТВЕННЫЙ
СТРОИТЕЛЬНЫЙ УНИВЕРСИТЕТ, 2000
Дискретная математика
Алгебра логики
Функции алгебры логики
Определение.
Функция
![]() ,
областью определения и областью
значений, которой является множество
,
областью определения и областью
значений, которой является множество
![]() ,
называется функцией алгебры логики
или булевой функцией . Функцию алгебры
логики можно задать в виде таблицы :
,
называется функцией алгебры логики
или булевой функцией . Функцию алгебры
логики можно задать в виде таблицы :
|
|
0 0………. 0 0 0 0 ……… 0 1 0 0 ……… 1 0 ………………… 1 1 1 1 |
………………..
|
Будем
обозначать через
![]() систему всех функций алгебры логики .
систему всех функций алгебры логики .
Теорема
. Число
![]() всех
функций из
всех
функций из
![]() ,
зависящих от
,
зависящих от
![]() переменных
переменных
![]() равно
равно
![]() .
.
Введем функции алгебры логики, которые будем называть элементарными :
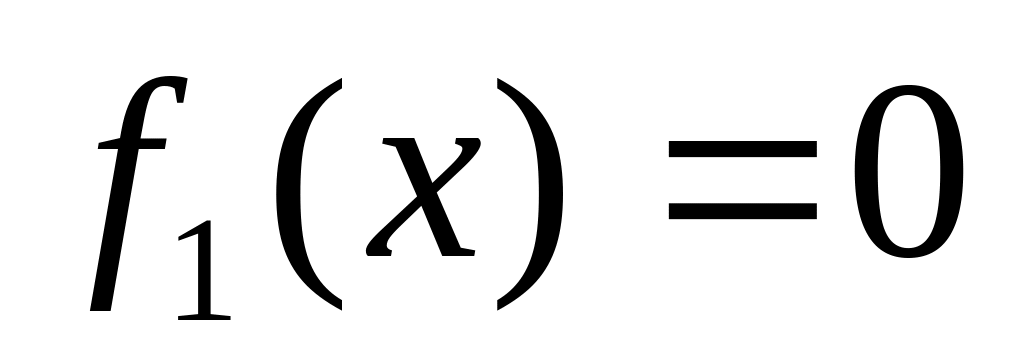 .
.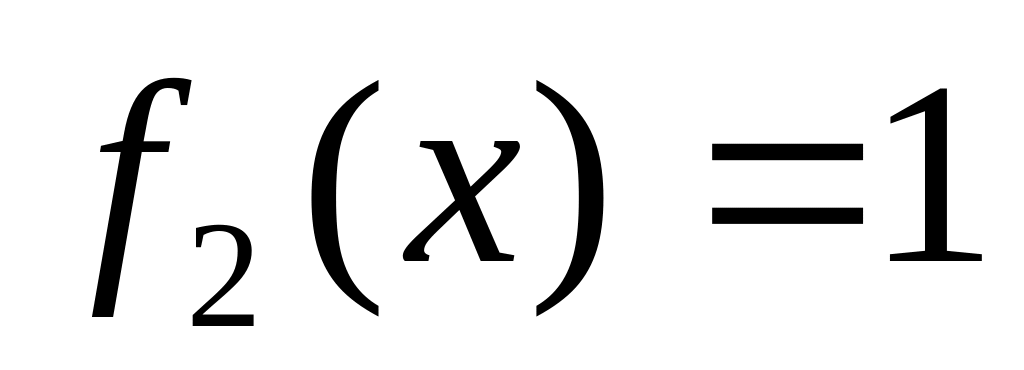 .
.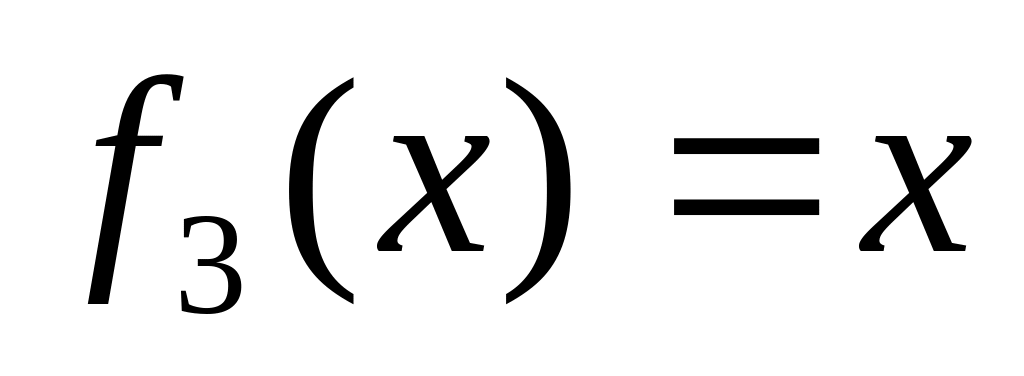 .
.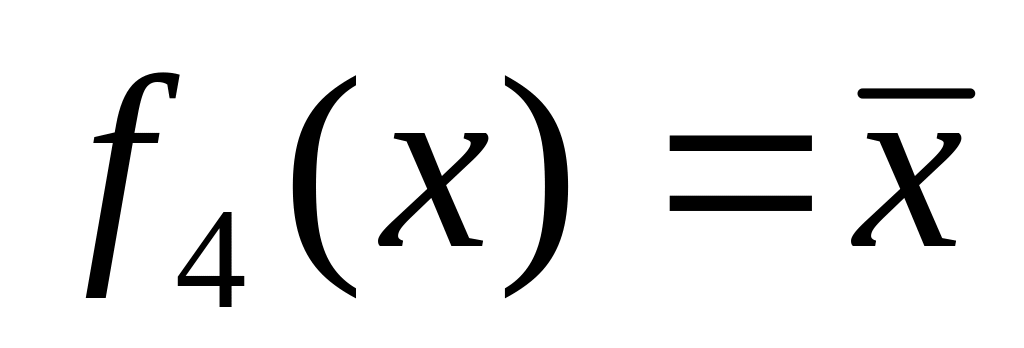 -
отрицание
-
отрицание
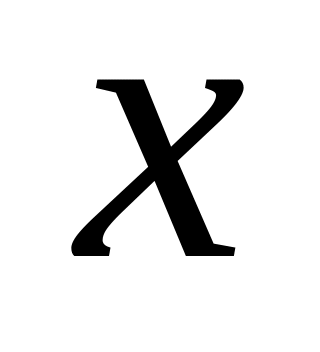 .
.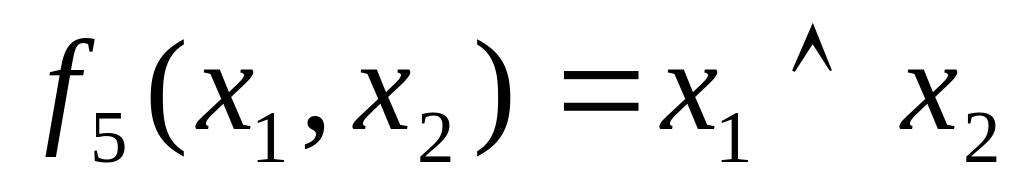 -
конъюнкция
-
конъюнкция
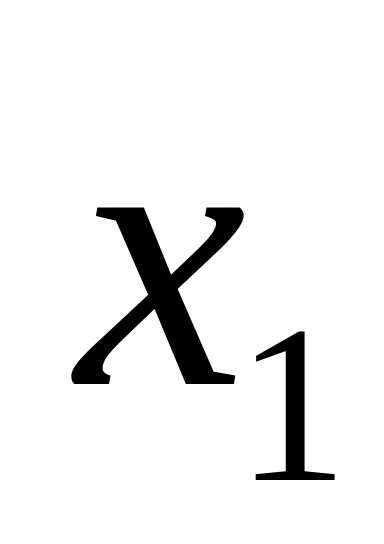 и
и
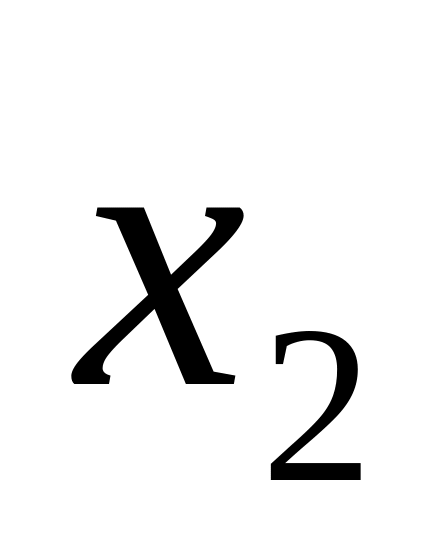 .
.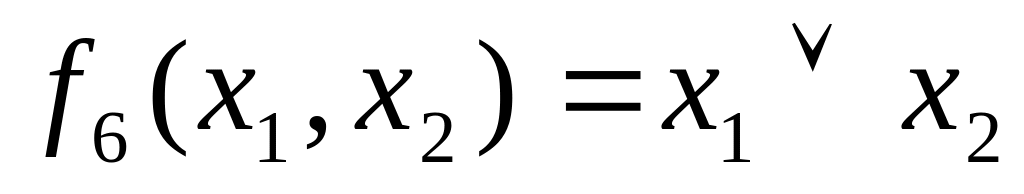 -
дизъюнкция
и
.
-
дизъюнкция
и
.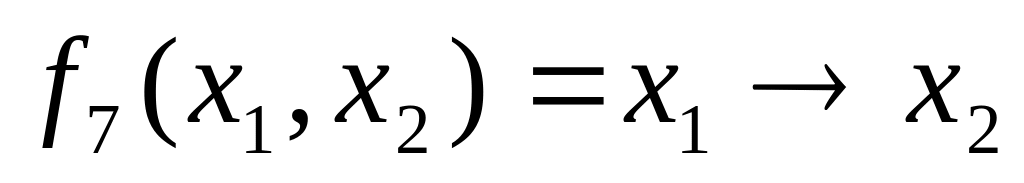 -
импликация
и
.
-
импликация
и
.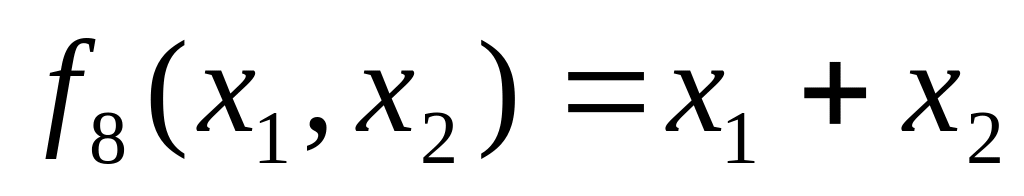 -
сложение
и
по mod 2 .
-
сложение
и
по mod 2 .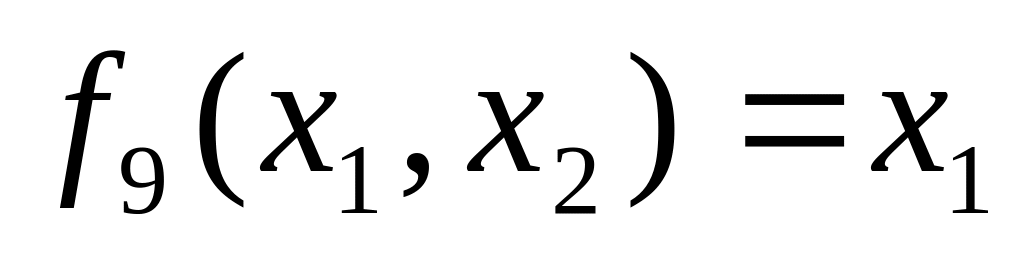 /
- функция
Шеффера .
/
- функция
Шеффера .
Для последних двух функций укажем соответствующие значения :
|
|
|
0 0 0 1
1 1 |
0 1 1 0 |
1 1 1 0 |
Реализация функций формулами
Дадим рекурсивное определение формулы .
Пусть D – подмножество функций из .
Каждое
выражение
![]() , где
, где
![]() D
, называется
формулой над D
.
D
, называется
формулой над D
.
Пусть
![]() функция из D
и
функция из D
и
![]() -
выражения , являющиеся либо формулами
над D
, либо
символами переменных , тогда выражение
-
выражения , являющиеся либо формулами
над D
, либо
символами переменных , тогда выражение
![]() называется
формулой над
называется
формулой над
![]() .
.
Пусть D – множество элементарных функций . Следующие выражения являются формулами над D :
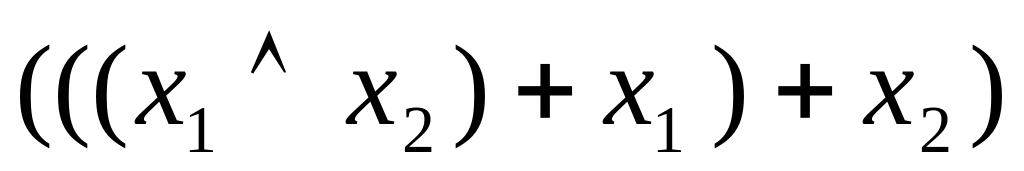 ,
,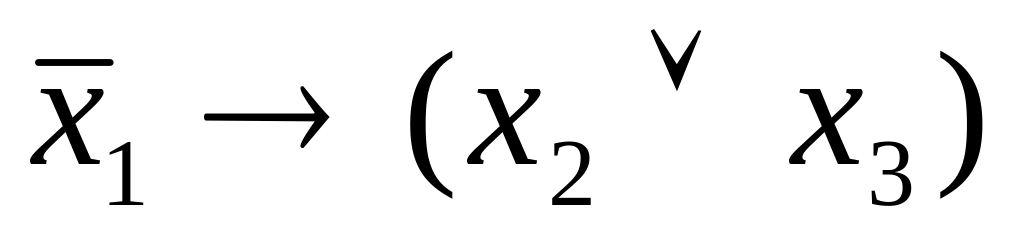 .
.
Будем
в дальнейшем использовать следующую
запись
![]() , которая
означает , что формула U
построена из
, которая
означает , что формула U
построена из
![]() .
В тех случаях , когда нужно обратить
внимание на множество переменных ,
которые участвуют в построении формулы
, пишут
.
В тех случаях , когда нужно обратить
внимание на множество переменных ,
которые участвуют в построении формулы
, пишут
![]() .
.
Формулы , которые использовались для построения формулы U , будем называть подформулами формулы U.
Каждой
формуле
![]() над
можно поставить в соответствие функцию
из
.
над
можно поставить в соответствие функцию
из
.
Если
функция
![]() соответствует
формуле
соответствует
формуле
![]() , то говорят , что формула
реализует функцию
.
, то говорят , что формула
реализует функцию
.
Функцию , соответствующую формуле , будем называть суперпозицией функций из .
Формулы
и
![]() называются эквивалентными , если
соответствующие им функции
называются эквивалентными , если
соответствующие им функции
![]() и
и
![]() равны .
равны .
Полнота и замкнутость
Система
функций
![]() из
называется полной , если любая булева
функция может быть записана в виде
формулы через функции этой системы .
из
называется полной , если любая булева
функция может быть записана в виде
формулы через функции этой системы .
Примеры полных систем :
Система .
Система
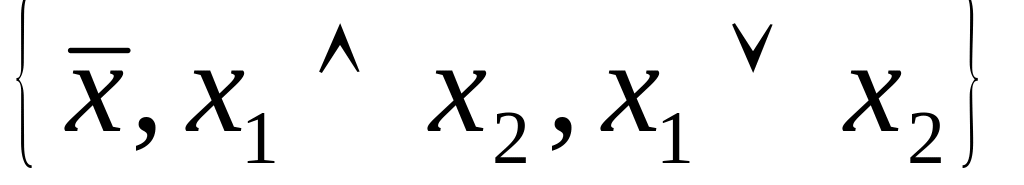 .
.
Теорема
. Пусть даны две системы функций из
![]()
![]() ,
,
![]() ,
,
относительно которых известно , что первая система полна и каждая ее функция выражается через функции второй системы ,тогда и вторая система также полной.
Опираясь на эту теорему можно установить полноту еще ряда систем .
Теорема
. Каждая
функция из
может быть выражена при помощи полинома
по mod
2 – полинома
Жегалкина :
![]() ,
где
,
где
![]() или
или
![]() .
.
Пусть
![]() -
некоторое подмножество функций из
.
Замыканием
называется множество всех булевых
функций , представимых в виде формул
через функции множества
и
обозначается
-
некоторое подмножество функций из
.
Замыканием
называется множество всех булевых
функций , представимых в виде формул
через функции множества
и
обозначается
![]() .
.
Пример .
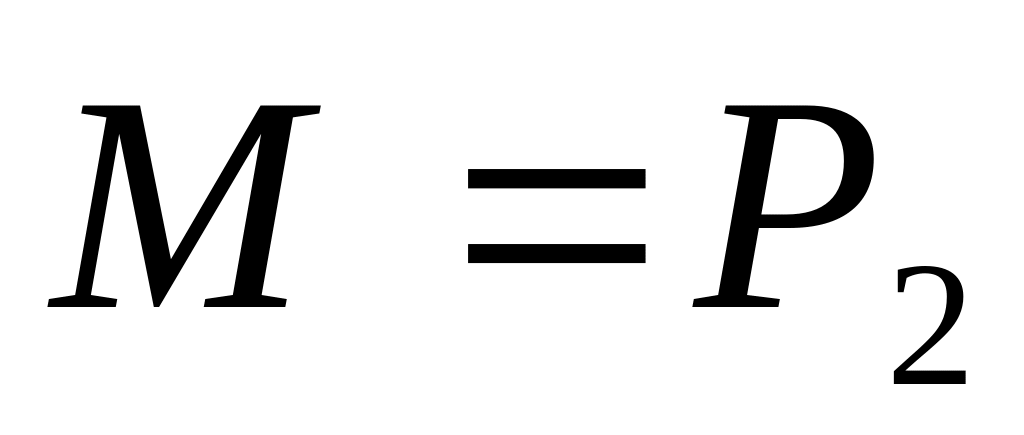 .
Очевидно , что
.
Очевидно , что
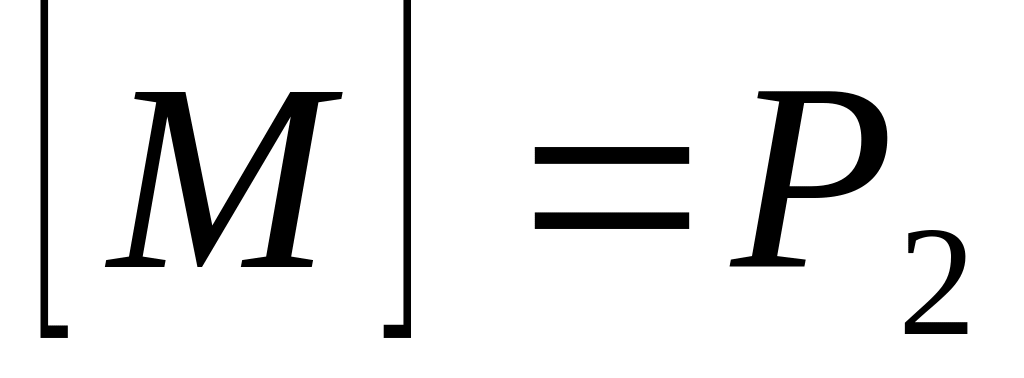 .
.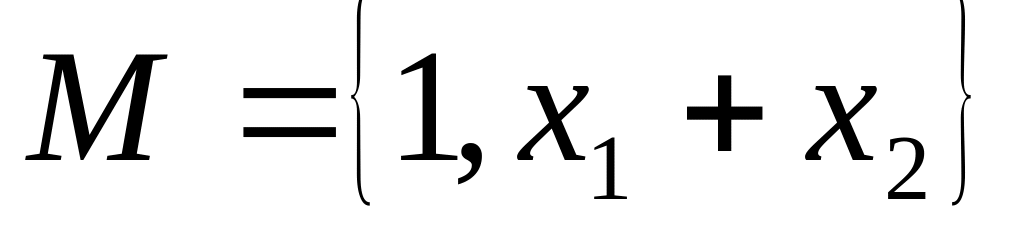 .
.
Замыканием
этого множества будет класс
![]() всех
линейных функций , т.е.
всех
линейных функций , т.е.
функций
, имеющих вид :![]() . где
. где
![]() или
.
или
.
Отметим некоторые свойства замыкания :
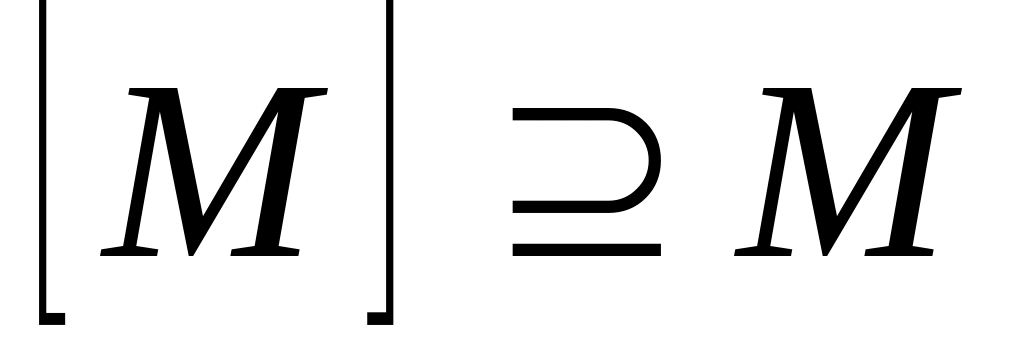 .
.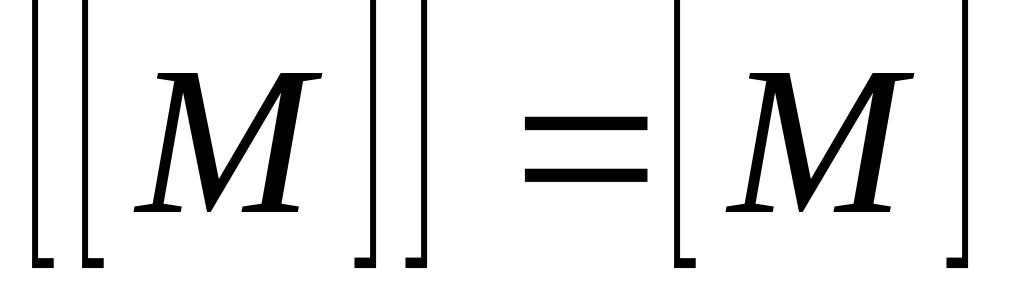 .
.Если
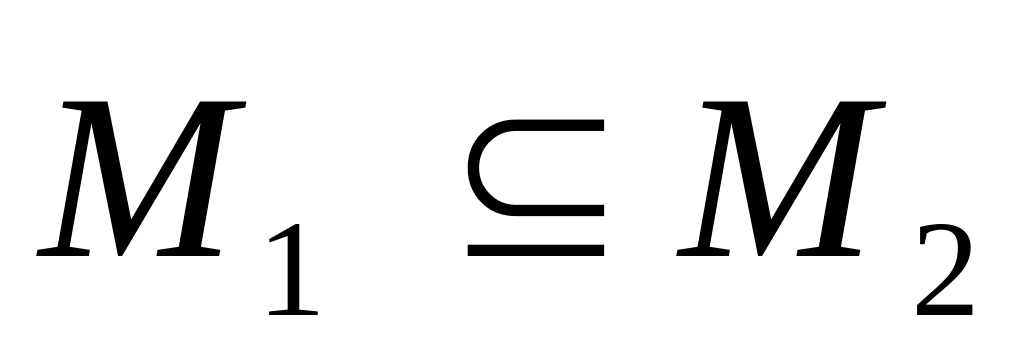 , то
, то
 .
.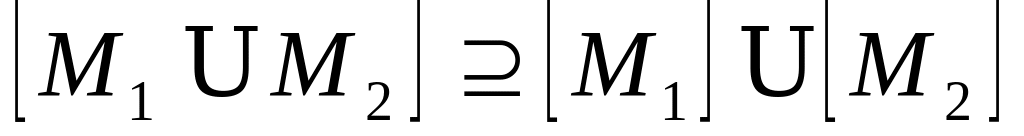 .
.
Класс
функций М
называется замкнутым , если
![]() .
.
Пример .
Класс
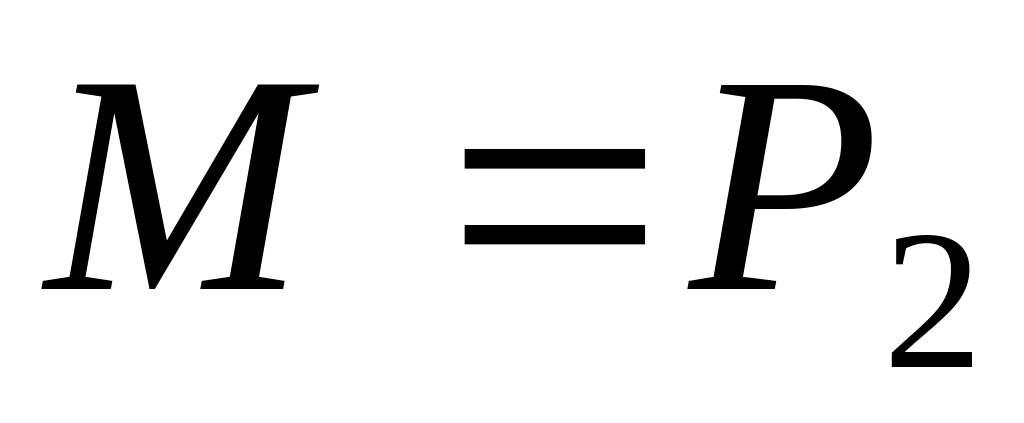 является замкнутым .
является замкнутым .Класс
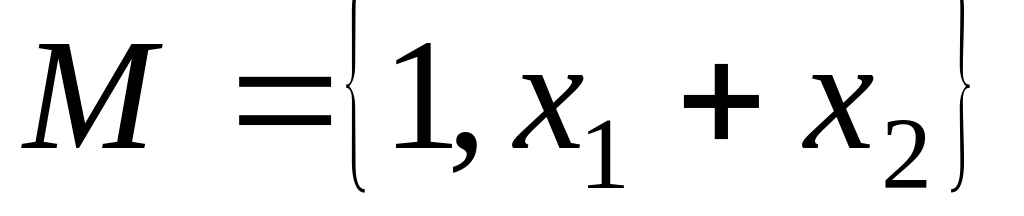 не замкнут .
не замкнут .Класс L замкнут .
Исходя из данных определений можно сказать , что система М – полная , если
.
