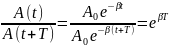6. Основное уравнение динамики вращательного движения твердого тела. Закон сохранения момента импульса.

Изменение момента количества движения твердого тела , равно импульсу момента всех внешних сил, действующих на это тело.

Закон сохранения момента импульса - физический закон, в соответствии с которым момент импульса замкнутой системы относительно любой неподвижной точки не изменяется со временем.

Зако́н сохране́ния моме́нта и́мпульса (закон сохранения углового момента) — векторная сумма всех моментов импульса относительно любой оси для замкнутой системы остается постоянной в случае равновесия системы. В соответствии с этим, момент импульса замкнутой системы относительно любой неподвижной точки не изменяется со временем.

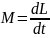- основное уравнение динамики вращательного движения твердого тела

7. Свободные незатухающие механические колебания.

Незатухающие колебания создаются такими устройствами, которые сами могут поддерживать свои колебания за счет некоторого постоянного источника энергии. Такие устройства называются автоколебательными системами.

К примеру, колебание пружинного маятника, которое само по себе затухало бы, поддерживается периодическими толчками, обусловленными самим колебанием маятника. При каждом толчке батарея отдает порцию энергии, часть которой идет на подъем груза. Система сама управляет действующей на нее силой и регулирует поступление энергии из источника — батареи. Колебания не затухают именно потому, что за каждый период от батареи отбирается как раз столько энергии, сколько расходуется за то же время на трение и другие потери. Что же касается периода этих незатухающих колебаний, то он практически совпадает с периодом собственных колебаний груза на пружине, т. е. определяется жесткостью пружины и массой груза.

Гармоническими называются колебания, при которых смещение точки от равновесия зависит от времени по закону sin или cos.

Однородное дифференциальное уравнение:

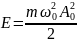
8. Физический и математический маятники. Уравнение колебаний.

Математическим маятником называется материальная точка, подвешенная на нерастяжимой невесомой нити, совершающая колебательное движение в одной вертикальной плоскости под действием силы тяжести.

Период колебаний математического маятника зависит от его длины и ускорения силы тяжести и не зависит от амплитуды колебаний.

Физическим маятником называется твердое тело, закрепленное на неподвижной горизонтальной ocи (оси подвеса), не проходящей через центр тяжести, и совершающее колебания относительно этой оси под действием силы тяжести. В отличие от математического маятника массу такого тела нельзя считать точечной.

Данная формула определяет приведенную длину физического маятника, т.е. длину такого математического маятника, период колебаний которого равен периоду колебаний данного физического маятника.

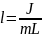
Энергия колебаний пропорциональна квадрату собственной частоты и квадрату амплитуды колебаний.

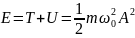
9. Свободные затухающие механические колебания. Коэффициент и логарифмический декремент затухания.

Гармонический осциллятор (в классической механике) — это система, которая при смещении из положения равновесия испытывает действие возвращающей силы, пропорциональной смещению.

Если осциллятор предоставлен сам себе, то говорят, что он совершает свободные колебания. Если же присутствует внешняя сила (зависящая от времени), то говорят, что осциллятор испытывает вынужденные колебания.

Механическими примерами гармонического осциллятора являются математический маятник (с малыми углами отклонения), груз на пружине, торсионный маятник и акустические системы.

Классический гармонический осциллятор – система совокупных гармонических колебаний.

– ускорение

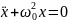
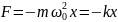
Следовательно, коэффициент затухания β есть физическая величина, обратная времени, в течение которого амплитуда уменьшается в е раз.

Следовательно, логарифмический декремент затухания χ есть физическая величина, обратная числу колебаний, по истечении которых амплитуда А уменьшается в e раз.

Натуральный логарифм отношения амплитуд, следующих друг за другом через период Т, называется логарифмическим декрементом затухания χ.

Отношение значений амплитуды затухающих колебаний в моменты времени t и t+T