7. Прямой изгиб. Силовая плоскость , нейтральный слой, закон Гука при чистом изгибе,нормальные напряжения, касательные напряжения. Условия прочности.

Изгибом называется такой вид деформации при котором в поперечном сечении стержня возникают изгибающие моменты, если при этом все остальные внутренние силовые факторы =0, изгиб называется чистым.

Плоскость, в которой на брус приложены внешние нагрузки называется силовой плоскостью.

Верхние волокна балки растягиваются, а нижние сжимаются и поэтому на Y нейтральной линии деформации не наблюдаются.

Плоскость, проходящая через нейтральную линию называется нейтральным слоем.

растяжение

н ейтральная линия

сжатие

Выделим из бруса некоторый элементарный элемент шириной dz, будем считать что при изгибе левая плоскость останется неподвижной, а правая повернется на некоторый угол:

АВ=СD=C¹D¹

CD-нейтральный слой

C¹D¹=ρdϴ

A¹ B¹=(ρ+y) dϴ относительная деформация будет:

Тогда в силу допущения о ненадавливаемости продольных волокон, закон Гука будет иметь вид: где, ρ-радиус кривизны

σ- нормальное напряжение

Отсюда, нормальные напряжения изменяются по сечению бруса линейно и достигают максимального значения в крайних точках сечения.

Максимальное значение нормальных напряжений будет равно:

σ_мах= М_ху_мах/Y_x= M_х/W_х

Формула является основной в расчетах на прочность при изгибе. Она показывает, что наиб.экономичным, являютя такие формы поперечных сечений для которых с наименьшими затратами материалов получается наибольшая величина моментов сопротивлений.

Величина касательных напряжений определяется по формулам Журавского:

τ=QyS ^*x/Y_xb, где

b - ширина сечения,

Q_y – абсолютная величина поперечной силы в том сечении, где вычисляются касательные напряжения,

S_x^*-Абсолютная величина статического момента отсеченной части поперечного сечения относительно нейтральной оси (линии),

У_х- момент инерции сечения относительно нейтральной оси.

Условие прочности при изгибе формулируется следующим образом: Балка будет прочной, если максимальные нормальные напряжения не превысят допускаемых напряжений

8.Геометрические характеристики плоских сечений. Статический момент, осевой и полярный момент инерции, центробежный момент инерции, момент сопротивления. Изменение моментов инерции при параллельном переносе и при повороте осей координат. Геометрические характеристики – числовые величины (параметры), определяющие размеры, форму, расположение поперечного сечения однородного по упругим свойствам деформируемого элемента конструкции (и, как следствие, характеризующие сопротивление элемента различным видам деформации).

Площадь сечения является одной из геометрических характеристик, используемых, главным образом, в расчетах на растяжение и сжатие.

Площадь, ограниченная произвольной кривой, есть

Для вычисления геометрических характеристик сложных сечений, состоящих из простейших фигур, они разбиваются на конечное число n простейших частей. В этом случае

Для сечений, составленных из профилей стандартного проката, площадь каждого профиля и остальные необходимые для расчетов размеры принимаются по таблицам ГОСТов на прокатную сталь.

Статическим моментом плоского сечения относительно некоторой оси называется, взятая по всей его площади А, сумма произведений площадей элементарных площадок dA на их расстояния от этой оси (рис. 4.1):

где yc – расстояние от центра тяжести всего плоского сечения до оси x; xc – расстояние от центра тяжести всего сечения до оси y.

Статический момент( размерность м3) сложного сечения относительно некоторой оси равен сумме статических моментов всех частей этого сечения относительно той же оси:

Из выражений (4) можно определить координаты центра тяжести плоского сечения:

(7)

Для сложного поперечного сечения формулы (7) можно представить в следующем виде

Осевым( экваториальным) моментом инерции сечения относительно некоторой оси х и у называется взятая по всей площади А сумма произведений элементарных площадок dA на квадраты их расстояний до этой оси

Где х и у-расстояние от элементарной площадки, выбранной в пределах данного сечения, до соответствующей оси.

Полярным моментом инерции сечения относительно некоторого полюса(точки) называется взятая по всей площади А сумма произведений элементарных площадок dA на квадраты их расстояний до этого полюса ρ

I_ρ=ᶋρ²dA

Центробежным моментом инерции сечения относительно двух взаимно перпендикулярных осей х и у называется взятая по всей площади А сумма произведений элементарных площадок А на расстояние до этих осей

Осевым моментом сопротивления сечения называется частное от деления осевого момента, на расстояние уmax или хмах от рассматриваемой оси до наиболее удаленной точки сечения

Wx=Ix/ymax , Wy=Iy/xmax

С изменением положения системы координат изменяются по величине геометрические характеристики сечений. При параллельном переносе осей координат осевые и центробежный моменты преобразуются в соответствии с формулой Гюйгенса и определяются из выражений:

а и b- расстояние между горизонтальными и вертикальными осями соответственно, при этом оси ч и н проходят через центр тяжести сечения.

Для теоретического определения положения центра тяжести сложного сечения его разбивают на простые фигуры (прямоугольник, треугольник, круг, полукруг). Координаты центра тяжести определяются по известным из теоретической механики зависимостям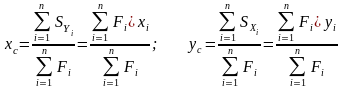 где xc, yc – координаты центра тяжести сложной фигуры;

xi, yi, – координаты центров тяжести простейших фигур, на которые разбито сечение, подставляются в выражения (5.8) с учетом знаков.

Две взаимно перпендикулярных оси, относительно которых центробежный момент инерции равен нулю, называются главными осями инерции, а осевые моменты инерции относительно этих осей – главными центральными моментами инерции.

9.Косой изгиб. Нормальные напряжения, уравнения нейтральной линии. Условие прочности при косом изгибе.

Косой изгиб-такой вид деформированипя, при котором плоскость изгибающего момента не совпадает ни с одной из главных осей поперечного сечения (рис. 5.27, а). Косой изгиб удобнее всего рассмотреть как одновременный изгиб бруса относительно главных осей x и y поперечного сечения бруса.

Нормальное напряжение определяется как сумма нормальных напряжений, возникающих от действия каждого из моментов:

, где

I_x и I_y- главные центральные моменты инерции сечения.

x и y- координаты точек, в к-х определяется напряжение.

уравнение представляет собой уравнение плоскости, если известен модуль , то уравнение примет вид:

.

Уравнение нейтральной линии, т.е. геометрического места точек, где нормальное напряжение принимает нулевые значения:

,

, где

x,y- координаты точек, лежащей на нулевой линии.

Из уравнения следует, что нейтральная линия всегда проходит через начало координат. Максимальные напряжения в сечении возникают в точках наиболее удаленных от нейтральной линии.

В общем случае нулевая линия не перпендикулярна к плоскости изгибающего момента. Она повернута к той главной оси, относительно которой момент инерции минимален. Компоненты изгибающего момента могут растягивать и сжимать волокна, поэтому в общем виде:

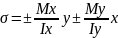
10. Изгиб с растяжением (сжатием)

Расчеты на совместное действие изгиба и растяжения можно свести к следующим двум основным видам:

а) расчеты на действие продольно-поперечных нагрузок;

б) расчеты на внецентренное растяжение (сжатие).

Отдельно должен быть рассмотрен изгиб с растяжением (сжатием) кривого бруса.

Сложный изгиб с растяжением (сжатием) прямого бруса. Если на балку действуют и продольные и поперечные нагрузки, пересекающие ось бруса, то в общем случае (рис. 10.19, а) в поперечных сечениях возникают изгибающие моменты Мz и Му в двух плоскостях, поперечные силы Qz и Qy, а также продольная сила N (рис. 10.19, б). Таким образом, в этом случае будет сложный изгиб с растяжением или сжатием.

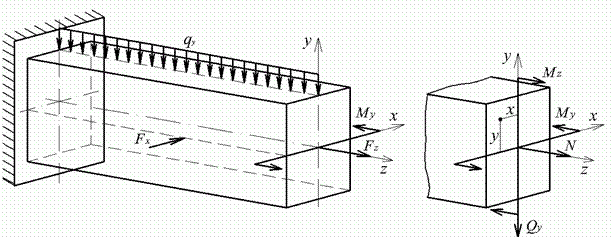
а б

Нормальное напряжение в произвольной точке сечения

(10.54)

Изгибающие моменты, продольную силу и координаты точки, в которой вычисляют напряжения, подставляют сюда с их знаками.

Пренебрегая касательными напряжениями от поперечных сил, можно считать, что напряженное состояние в опасной точке линейно. Следовательно, условие прочности имеет простейший вид:

(10.55)

Если сечение имеет две оси симметрии и выступающие углы, то опасной будет одна из угловых точек. Напряжения в ней определяют по формуле (10.54) или так: (10.56)

В случае плоского изгиба в главной плоскости уОх с растяжением (сжатием) трехчленная формула превращается в двучленную:

(10.57)

Эти формулы применяют при расчете на прочность плоских рам и арок малой кривизны. Опасными в этом случае являются те сечения, где действует наибольший изгибающий момент

При расчете брусьев с поперечным сечением произвольной формы для определения опасной точки сечения необходимо, прежде всего, установить положение нейтральной линии. Способ определения положения нейтральной линии описан ниже при рассмотрении внецентренного растяжения.

Внецентренное растяжение (сжатие) прямого бруса. Внецентренное растяжение (сжатие) представляет собой частный случай сложного изгиба с растяжением (сжатием), при котором брус растягивается силами, параллельными оси бруса, так что их равнодействующая не совпадает с осью бруса (рис. 10.21), а проходит через точку р, называемую полюсом силы.

Рис. 10.21. Внецентренное растяжение (сжатие)

Пусть на брус произвольного сечения действует одна сила F, параллельная оси бруса и пересекающая любое поперечное сечение в точке р (рис. 10.21). Координаты этой точки в системе главных осей сечения обозначим через и , а расстояние этой точки до оси х, называемое эксцентриситетом,— через е. В любом поперечном сечении при такой нагрузке действуют следующие внутренние силовые факторы:

Таким образом, напряжения в произвольной точке сечения будут складываться из напряжений осевого растяжения силой N и напряжений от чистого изгиба моментами и :

(10.59)

Внеся сюда вместо и их значения, получим

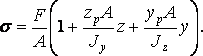(10.60)

Этой формуле можно придать несколько иной вид, выразив главные моменты инерции через радиусы инерции:

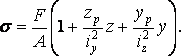(10.61)

Для определения опасной точки при сложном профиле целесообразно построить нейтральную линию сечения. Опасной в сечении будет точка, наиболее удаленная от нейтральной линии.

Уравнение нейтральной линии получим, приравняв к нулю правую часть уравнения (10.61) и обозначив координаты точек на нейтральной линии через и :

(10.62)

Полагая в этом уравнении поочередно и , найдем отрезки и , отсекаемые нейтральной линией на осях у и z (рис. 332):

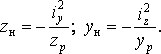(10.63)

Из зависимостей (10.63) следует, что нейтральная линия пересекает координатные оси в точках, принадлежащих квадранту, противоположному тому, в котором находится точка р

Теперь, проведя параллельно нейтральной линии касательные к контуру сечения, найдем наиболее напряженные точки A и B в растянутой и сжатой зонах сечения (рис. 10.22).

Рис. 10.22. Эпюра нормальных напряжений

Напряжения в этих точках и условия прочности имеют вид

(10.64)

Здесь zA, уА и -zB, -ув — координаты точек A и B соответственно. Эпюра напряжений приведена на рис. 10.22. Для прямоугольного сечения условие прочности удобнее представить в следующем виде:

(10.65)

Формулы (10.64) и (10.65) справедливы и в случае действия сжимающей силы F, если нет опасности возникновения продольного изгиба.