Статистическая и корреляционная зависимость.

Математический аппарат используется для описания зависимостей связанных не только функционально, то есть когда связь налицо (Пример: время реакции оператора пульта управления есть сумма времени поиска сигнала, времени принятия решения и времени совершения управляющих действий), но и статистически.

Определение 1. Функциональная зависимость величины Y от величины X - зависимость, при которой каждому значению величины X из множества возможных значений соответствует одно значение величины Y. Изменение значения величины X приводит к изменению значения величины Y.

Определение 2. Статистическая зависимость величины Y от величины X - зависимость, при которой каждому значению величины X из множества возможных значений соответствует некоторое множество возможных значений величины Y, характеризуемое определенным законом распределения. Изменение значения величины X приводит к изменению распределения величины Y, являющейся случайной при каждом фиксируемом значении величины X.

Пример. X - количество вводимого внутривенно препарата, его концентрация в крови Y в произвольный момент времени статистически зависит от величины X, так как определяется многими другими факторами.

В большинстве случаев исследователи ограничиваются рассмотрением частного случая статистических зависимостей - корреляционной зависимости между величинами, когда изменение одной величины (например X) влечет изменение математического ожидания другой (Y). Примером корреляционной зависимости может быть приведенный выше случай с препаратом и его концентрацией в крови; зависимость между ростом человека и массой его тела).

Корреляционная зависимость Y от X описывается уравнением:

М(Y)_x = F(x) (1)

М(Y)_x – условное математическое ожидание величины Y, соответствующее данному значению Х; х – отдельное значение величины Х; F(x) – некоторая функция. Уравнение (1) называют уравнением регрессии Y на Х.

Обратная корреляционная зависимость – уравнение регрессии Х на Y:

М(Х)_Y = Ф(у) (2)

М(Х)_Y – условное среднее значение величины Х, соответствующее данному значению Y; у – отдельное значение величины Y; Ф(у) – некоторая функция.

Графики функций F(x) и Ф(у) называют линиями регрессии. Если F(x) и Ф(у) в уравнениях (1) и (2) линейные, то их можно представить в виде:

М(Y)_x = Ах +В (3)

М(Х)_Y = Cy + D (4)

A,B,C,D – параметры; в этом случае корреляционные зависимости называются линейными, а их графики (линии регрессии) – прямые.

Корреляционная таблица.

Первым этапом статистической обработки величин является составление корреляционной таблицы.

Как она заполняется..

1. В первой строке перечисляются все встречающиеся в экспериментальной выборке значения величины X, т.е.

x_{1 ,}x_2,… x_i… x_k , где k – количество различных значений величины Х, i = 1,2,3…k.

2. В первом столбце перечисляются все встречающиеся в экспериментальной выборке значения Y, т.е.

y₁, y₂… y_j …y_l , где l – количество различных значений величины Y, j = 1,2,3,….,l.

3. На пересечении строк и столбцов указываются частоты n_ji , равные числу появлений в выборке пары (х_i;y_j ). Например, частота n₁₂ равна числу появлений в выборке пары (х₂ ;у₁ ).

4. В последнем столбце указываются числа n_yj равные количеству появления в выборке значения y_j, независимо в паре с каким из значений величины X оно появилось. Значение n_yj равно сумме частот соответствующих строк, т.е.:

n_yj = n_1j + n_2j +… n_ij …+ n_кj= ∑ n_ij , j = 1,2,…,k.

5) В последней строке указываются числа n_xi равные количеству появления в выборке значения x_i, независимо в паре с каким из значений величины Y оно появилось. Значение n_xi равно сумме частот соответствующих столбцов, т.е.:

n_xi = n_i1 + n_i2 +…+ n_ij +…+ n_il =∑ n_ij , i = 1,2,…,l.

6) В правой нижней клетке таблицы находится число N, равное объему выборки. Значение N равно сумме частот внутри корреляционной таблицы, и равно сумме значений последнего столбца и последней строки, т.е.

N = ∑ n_xi = ∑ n_yj

Корреляционная таблица содержит всю информацию, полученную в результате выборочных наблюдений величин Х и Y.

Таблица 1. Корреляционная таблица.

X Y	x1	x2	……	xi	…..	xk	ny
y1	n11	n12		n1i		n1k	ny1
y2	n21	n22		n2i		n2k	ny2
…..
yj	nj1	nj2		nji		njk	nyj
…..
yl	nl1	nl2		nli		nlk	nyl
nx	nx1	nx2		nxi		nxk	N

С помощью корреляционной таблицы для каждого значения х_i можно записать соответствующее эмпирическое распределение величины Y. В первой строке этой таблицы перечислены все встречающиеся в выборке значения величины Y, во второй — соответствующие частоты.

_{Таблица 2. Эмпирическое распределение величины Y для некоторого xi}

Y	y1	y2	…..	yj	….	yl
nyj	n1i	n2i		nji		nli

По данным таблицы 2 можно определить условные средние значения величины Y, соответствующие значениям Х = x_i, по формуле средней арифметической взвешенной

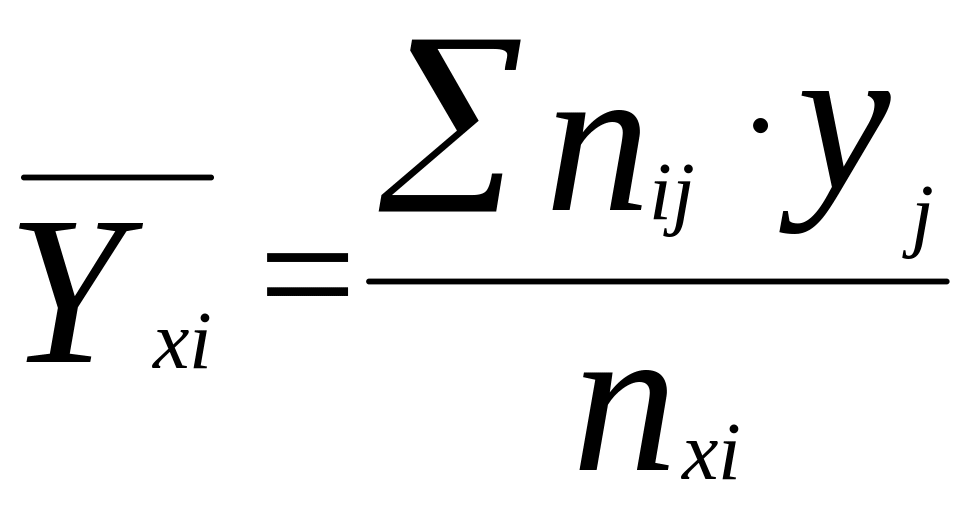(5)

По этой формуле можно определить значения , ,….. и составить таблицу, в первой строке которой – все встречающиеся в выборке значения величины Х, во второй – условные средние значения величины Y.

Таблица 3. Условные средние значения величины Y.

X	x1	x2	……	xi	…..	xk
			……….		………

Таблицу 3 можно рассматривать, как зависимость условного значения Y от X, т.е., как экспериментальную корреляционную зависимость.

Если построить полученные точки в системе координат, можно сделать предположение о форме корреляционной зависимости.

Например:

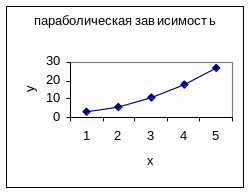
Уравнение прямых регрессии.

Если есть основания полагать, что между величинами Х и Y существует линейная корреляционная зависимость, то уравнения линейной регрессии Y на Х и Х на Y имеют вид (3) и (4). В данном случае вводят выборочные уравнения линейной регрессии Y на Х и Х на Y.

_x = ρ_Yx∙x +b (6)

_y = ρ_Xy∙y +d (7)

ρ_Yx, ρ_Xy – выборочные коэффициенты регрессии, соответственно А и С в уравнениях (3),(4). При этом средние _x и _y являются оценками условных средних математических ожиданий М(Y)_x и М(Х)_Y.

Для нахождения выборочных коэффициентов регрессии применяют метод наименьших квадратов, который заключается в следующем. Пусть результаты выборочных наблюдений корреляционной зависимости Y от X представлены в виде совокупности точек, указывающих на приблизительно линейный характер зависимости. В этом случае необходимо найти такие параметры уравнения (6), чтобы соответствующая прямая линия (линяя регрессии) проходила как можно ближе ко всем точкам совокупности, т.е. сумма квадратов отклонений ординат всех эмпирических точек от ординат теоретической прямой должна быть минимальной.Для лучшего усвоения рассмотрим метод наименьших квадратов графически.

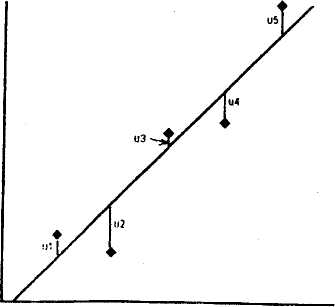
На рисунке представлена совокупность точек, указывающих на приблизительно линейный характер зависимости между величинами X и Y (линия регрессии на рисунке - прямая и точки выстраиваются вдоль этой линии). Отклонения ординат эмпирических точек от ординат точек теоретической прямой на рисунке обозначены как u₁, u₂,… В качестве «расстояния» от прямой до всех точек совокупности можно использовать величину U = u₁+u₂+…+u_k, где k – количество точек совокупности. Но в этом случае при больших значениях k ( при большом количестве точек) U будет стремиться к нулю, т.к. u_i будет принимать как положительные, так и отрицательные значения ( точки совокупности расположены как ниже, так и выше кривой). Для того чтобы избавиться от отрицательных значений u_i, их возводят в квадрат, т.е. U= u₁²+u₂²+…+u_k². Таким образом:

U = ∑n_xi ∙( (x_i) - _xj)², где

n_xi – число появлений в выборке значения х_i; (x_i) – значение, получаемое по формуле (6) при подстановке в нее значения х_i.

Функция U может быть представлена в виде:

U = ∑n_xi∙( ρ_Yx∙x_i +b - _xj)²

Из условия минимума сложной функции следует, что ее частные производные должны обращаться в нуль.

Таким образом получаем два уравнения для определения ρ_Yx и b:

(8)

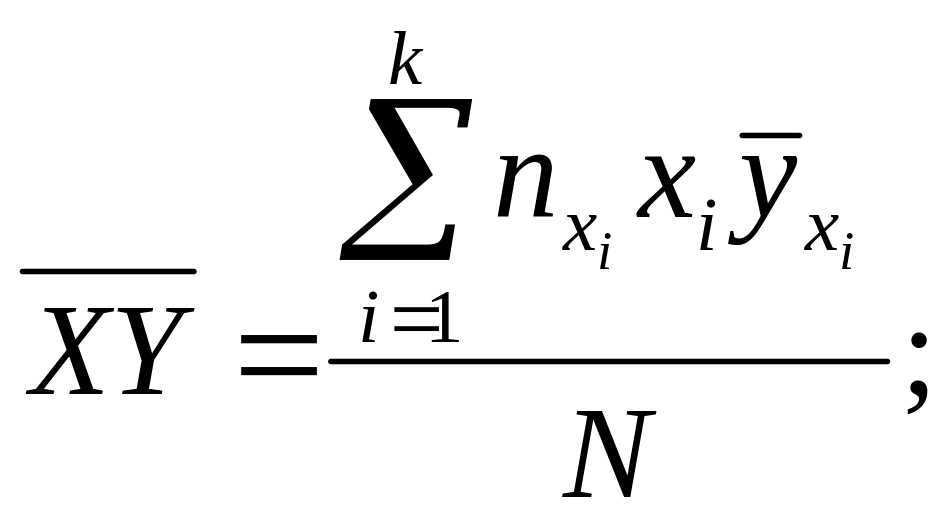
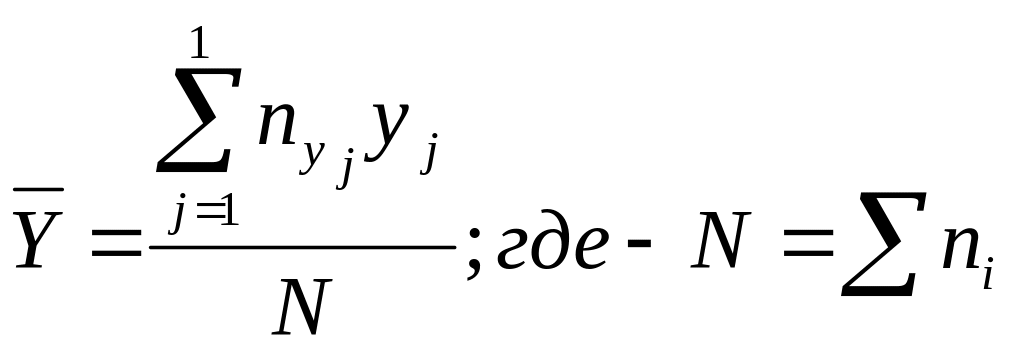
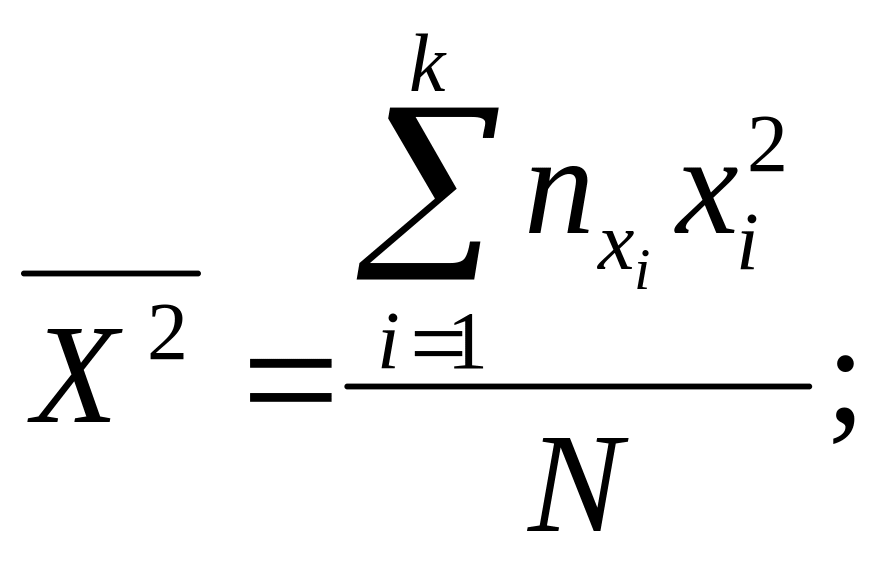
Аналогичным образом можно получить выражения для выборочного коэффициента регрессии Y на X.

Проанализируем сказанное графически.

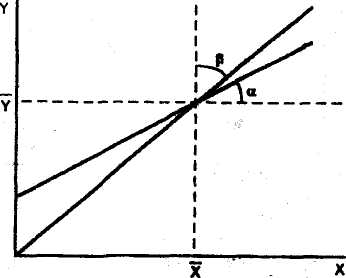
Линии выборочной регрессии и проходят через точку ( ; ).

При этом тангенс угла наклона прямой линии регрессии по отношению к оси Ох численно равен коэффициенту регрессии ρ_Yx, а тангенс угла β - коэффициенту регрессии ρ_Xy. Чем больше коэффициент ρ_Yx линейной регрессии Y на X, тем сильнее изменяется условное среднее значение величины Y при изменении величины X =» тем сильнее корреляционная связь.

Рассмотрим нахождение коэффициентов регрессии и составление уравнения прямой регрессии на примере:

Пример . Провели эксперимент, состоящий из двух этапов.

На первом этапе провели тест Кэттелла, X - результат испытуемого по шкале В (Интеллект). На втором этапе испутыемые в течение часа должны были решать математические задачи - всего 60 задач, Y - количество правильно решенных задач.

Задание: составить уравнение прямых регрессии Y на X и X на Y.

Решение.