9. Средние величины: понятие, виды.

Ср вел-й наз пок-ль, к-й харак-ет обобщенное зн-е признака или группы признаков в исследуемой сов-сти.

Если исследуется совок-сть с качественно однор признаками, то ср вел-на выступает здесь как типическая средняя - т.е. обобщает качественно однор зн-я признака в данной совок-сти, каковым явл доля расходов у работников данной группы на товары первой необходимости.

При исследовании сов-сти с качественно разнородными признаками на первый план может выступить нетипичность средних пок-й. Такими, к примеру, явл средние пок-ли произведенного нац дохода на душу населения (разные возрастные группы), ср пок-ли урожайности зерн-х культур по всей территории РФ (р-ны разных климатических зон и разных зерновых культур)и т.д. Здесь ср вел-ны обобщают качественно разнородные знач-я признаков или сист-х пространственных совок-стей (м/д сообщество, континент, гос-во, регион, район и т.д.) или динамич совок-стей, протяженных во времени (век, десятилетие, год, сезон и т.д.). Такие ср вел-ны наз системными средними.

Виды средних величин:

Выбор вида средней опр-ся эк-м содерж-ем опред пок-ля и исх д-х. В каж конкретном случае прим-ся одна из ср вели-н: ариф-я, гарм-я, геом-я, квадр-я и т.д.

Перечисленные средние относ к классу стеленных средних и объединяются общей формулой:где х - среднее знач-е исследуемого явл-я; т — показ-ль степени средней; х — текущ знач-е осредняемого признака; и - число признаков.В зав-ти от знач-я пок-ля степени т разл след виды степенных средних:при т = -1 — средняя гарм-я Хгар;при т = О — средняя геомет-я х_г;при т = 1 — средняя ариф-я х_ар ;при от = 2 — средняя квадратич хкв и т.д.

- св-во степ-х средних возрастать с повышением 1 пок-ля степени определяющей ф-ции наз в статистике правилом мажорантности средних.

Помимо степенных средних в статистич практике ис­п-ся средние структурные, в качестве кот-х рассматриваются мода и медиана.

10. Средняя арифметическая и средняя гармоническая величины.

Ср арифм-я – исп-ся, когда расчет осущ по несгруппир-м статистич д-м, где нужно получить среднее слагаемое. Ф-ла ср ариф-й имеет вид

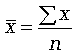, где n – числ-сть совок-сти.

Необх знать св-ва ариф-й средней, что очень важно как для ее исп-я, так и при ее расчете. Можно выделить три осн св-ва, к-е наиболее всего обусловили шир применение ариф-й средней в статистико-эк-х расчетах.

1: сумма полож-х отклонений индивид зн-й признака от его ср зн-я равна сумме отриц отклонений. Это очень важ св-во, поскольку оно пок-ет, что любые отклонения (как с +, так и с -), вызванные случ причинами, взаимно будут погашены.

2: сумма квадратов отклонений индивид зн-й признака от средней ариф-й меньше, чем от любого другого числа (а), т.е. есть число минимальное.

3: ср ариф-я пост вел-ны равна этой постоянной: при а = const.

Кроме этих 3-х важнейших св-в ср ариф-й сущ расчетные св-ва:

- если индивид зн-е признака каждой ед-цы умножить или разделить на пост число, то ср ариф-я увел-ся или

уменьшится во столько же раз;

- ср ариф-я не изм-ся, если вес (частоту) каждого зн-я признака разделить на постоянное число;

- если индив-е зн-я признака каж ед-цы уменьшить или увеличить на одну и ту же вел-ну, то ср

ариф уменьшится или увеличится на ту же самую вел-ну.

Средняя гарм-я - наз обратной ср ар-й, поскольку эта величина используется при k = -1.

Простая ср гарм-я исп-ся тогда, когда веса знач-й признака одинаковы. Ее ф-лу можно вывести из базовой ф-лы, подставив k = -1: