
МИНИСТЕРСТВО ОБРАЗОВАНИЯ И НАУКИ РФ
ФЕДЕРАЛЬНОЕ ГОСУДАРСТВЕННОЕ БЮДЖЕТНОЕ УЧРЕЖДЕНИЕ
высшего профессионального образования
«Национальный исследовательский ядерный университет» МИФИ
___________________________________________
Волгодонский инженерно-технический институт
Н.В. Ермолаева, А.Ю. Смолин
Физика
Учебное пособие
к выполнению индивидуальных домашних заданий для студентов очной
формы обучения
Волгодонск, 2011
1.2 Молекулярная физика. Термодинамика
Количество вещества системы (в молях) равно
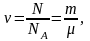
где N – число частиц системы; NA – число Авогадро; m – масса; – молярная масса.
Если система представляет смесь нескольких газов, то количество вещества системы равно
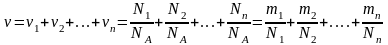 ,
,
где i , Ni , mi , i — соответственно количество вещества, число молекул, масса, молярная масса i-й компоненты смеси.
Молярная масса вещества равна
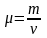 .
.
Молярная масса смеси газов вычисляется по формуле

где
 — масса i
- го компонента смеси;
— масса i
- го компонента смеси;
 —
количество вещества i
- го компонента смеси; п
— число
компонентов смеси.
—
количество вещества i
- го компонента смеси; п
— число
компонентов смеси.
Массовая доля i i - го компонента смеси газа (в долях единицы или в процентах) равна
 ,
,
где т — масса смеси.
Концентрация молекул (число частиц в единице объема) равна
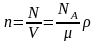 ,
,
где N —число частиц, содержащихся в данной системе; — плотность вещества; NА – постоянная Авогадро. Формула справедлива для любого агрегатного состояния вещества.
Уравнение
Клапейрона—Менделеева
(уравнение состояния идеального газа)
имеет вид pV
=
где т – масса газа; – молярная масса газа; R – универсальная газовая постоянная; =m/ – количество вещества; Т – термодинамическая температура.
Опытные законы идеального газа, являющиеся частными случаями уравнения Клапейрона—Менделеева для изопроцессов, имеют вид:
а) закон Бойля—Мариотта (изотермический процесс при T=const; m=const; =const)
pV = const
или для двух состояний газа
P1V1=p2V2,
где p1 и V1 — давление и объем газа в начальном состоянии; p2 и V2 — те же величины в конечном состоянии;
б) закон Гей-Люссака (изобарический процесс при p=const; m=const; =const)
V/T=const
или для двух состояний
V1/T1=V2/T2,
где V1 и T1— объем и температура газа в начальном состоянии; V2 и Т2 — те же величины в конечном состоянии;
в) закон Шарля (изохорический процесс при V=const; m=const; =const)
р/T=const
или для двух состояний
p1/T1=p2/T2,
где p1 и T1 — давление и температура газа в начальном состоянии; p2 и T2 — те же величины в конечном состоянии;
г) объединенный газовый закон ( при m=const ; =const)
pV/T= const
или для двух состояний
p1V1/T1 = p2V2/Т2 ,
где p1, V1 , T1 — давление, объем и температура газа в начальном состоянии; p2, V2 , T2 – те же величины в конечном состоянии.
Закон Дальтона, определяющий давление смеси газов, имеет вид
р =р1+p2+...+ pi+...+pn,
где pi—парциальные давления компонентов смеси; n – число компонентов смеси.
Основное уравнение кинетической теории газов имеет вид
 ,
,
где
 — средняя кинетическая энергия
поступательного движения молекулы
идеального газа.
— средняя кинетическая энергия
поступательного движения молекулы
идеального газа.
Средняя кинетическая энергия поступательного движения молекулы равна
=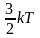 ,
,
где k — постоянная Больцмана.
Средняя полная кинетическая энергия молекулы равна
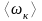 =
=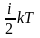 ,
,
где i — число степеней свободы молекулы.
Зависимость давления газа от концентрации молекул и температуры имеет вид
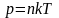 .
.
Распределение Больцмана (распределение молекул газа, находящегося во внешнем силовом поле) имеет вид
 ,
,
где n – концентрация молекул газа; U – потенциальная энергия молекулы; n0 – концентрация молекул в точках поля, где U=0; k – постоянная Больцмана; T – термодинамическая температура; e – основание натурального логарифма.
Распределение Максвелла молекул газа по скоростям теплового движения выражается соотношением
 ,
,
где f(V) – функция Максвелла; N – общее число молекул; dN(V) – число молекул, скорости которых лежат в интервале от V до V+dV; m – масса молекулы.
Скорости молекул определяются формулами:
а)
средняя квадратичная
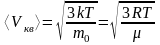 ;
;
б)
средняя арифметическая
 ;
;
в)
наиболее вероятная
 ,
,
где
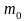 — масса
одной молекулы.
— масса
одной молекулы.
Удельные
теплоемкости
газа при постоянном объеме
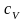 и при постоянном давлении
и при постоянном давлении
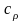 равны:
равны:
 ,
,
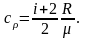
Связь между удельной с и молярной C теплоемкостями имеет вид
 .
.
Уравнение Майера имеет вид
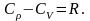
Внутренняя энергия идеального газа равна
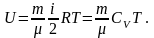
Первое начало термодинамики в общем случае записывается в виде
 ,
,
где
Q—
количество теплоты, сообщенное системе;
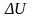 —
изменение внутренней энергии системы;
А — работа,
совершенная системой против внешних
сил.
—
изменение внутренней энергии системы;
А — работа,
совершенная системой против внешних
сил.
Работа расширения газа равна
 .
.
При изобарическом процессе работа газа равна
 .
.
При изотермическом процессе работа газа определяется формулой
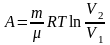
При адиабатическом процессе работа газа равна
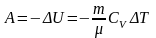 ,
,
или
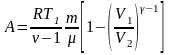 ,
,
где
 —
показатель
адиабаты.
—
показатель
адиабаты.
Уравнения Пуассона, связывающие начальные и конечные параметры идеального газа при адиабатическом процессе, имеют следующий вид:
 ;
;
 ;
;
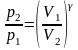 ;
;
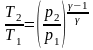 .
.
Термический коэффициент полезного действия цикла определяется формулой
 ,
,
где Q1— теплота, полученная рабочим телом от нагревателя; Q2— теплота, переданная рабочим телом охладителю.
Термический коэффициент полезного действия цикла Карно равен
 ,
,
где
T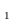 и T
и T — термодинамические температуры
нагревателя
и охладителя
соответственно.
— термодинамические температуры
нагревателя
и охладителя
соответственно.
Энтропия термодинамической системы может быть вычислена по формуле Больцмана:
 ,
,
где S – энтропия; W – термодинамическая вероятность состояния системы; k – постоянная Больцмана.
Изменение энтропии равно:
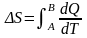 ,
,
где А и В – пределы интегрирования, соответствующие начальному и конечному состояниям системы.
Уравнение состояния реального газа (уравнение Ван-дер-Ваальса) имеет вид
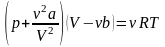 ,
,
где a и b – постоянные Ван-дер-Ваальса.
Коэффициент поверхностного натяжения жидкости равен
 или
или

где
F
— сила поверхностного натяжения,
действующая на контур, ограничивающий
поверхность жидкости;
 E
—изменение
свободной поверхностной энергии пленки
жидкости, связанное с изменением площади
S
поверхности этой пленки.
E
—изменение
свободной поверхностной энергии пленки
жидкости, связанное с изменением площади
S
поверхности этой пленки.
Формула Лапласа, выражающая давление p , создаваемое сферической поверхностью жидкости, имеет вид
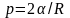 ,
,
где R — радиус сферической поверхности.
Высота подъема жидкости в капиллярной трубке определяется формулой
 ,
,
где
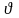 — краевой угол (
= 0 при полном смачивании стенок трубки
жидкостью;
=
при полном несмачивании); R—радиус
канала трубки;
— краевой угол (
= 0 при полном смачивании стенок трубки
жидкостью;
=
при полном несмачивании); R—радиус
канала трубки;
 — плотность жидкости; g
— ускорение
свободного падения.
— плотность жидкости; g
— ускорение
свободного падения.
Высота подъема жидкости между двумя близкими и параллельными друг другу плоскостями равна
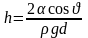 ,
,
где d — расстояние между плоскостями.
