3.2 Теорема Котельникова

Эта теорема (доказана академиком Котельниковым В.А. в 1933 г.), устанавливает возможность сколь угодно точного восстановления мгновенных значений сигнала с ограниченным спектром, исходя из отсчетных значений (выборок), взятых через равные промежутки времени.

Любые два сигнала с ограниченным спектром, принадлежащие семейству (3.9)

являются ортогональными если установить сдвиг

Путём соответствующего выбора амплитудного множителя А можно добиться того, чтобы норма каждого из этих сигналов стала единичной. В результате будет построен ортонормированный базис, позволяющий разложить произвольный сигнал с ограниченным спектром в обобщённый ряд Фурье. Из семейства функции достаточно рассмотреть лишь функциюприk=0.

(3.10)

так как норма любого сигнала одинакова независимо от сдвига во времени. Определим квадрат нормыи проинтегрируем поt.

Функции будут ортонормированными, если:

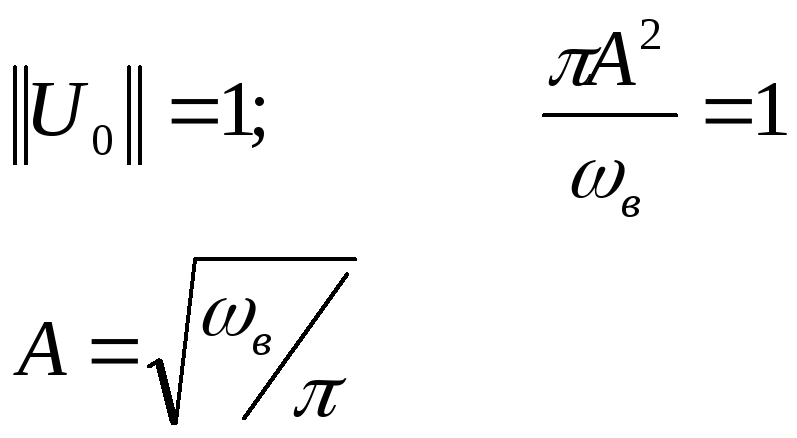(3.11)

Бесконечная совокупность функций.

(3.12)

образует базис Котельникова в линейном пространстве низкочастотных сигналов со спектрами, ограниченными сверху значением . Отдельная функция называетсяk-той отсчётной функцией. Если произвольный сигнал, спектральная плотность которого отлична от нуля лишь в полосе частотто его можно разложить в обобщенный ряд Фурье по базису Котельникова:

(3.13)

Коэффициентами ряда служат, как известно, скалярные произведения разлагаемого сигнала и k-той отсчётной функции:

(3.14)

Удобный способ вычисления этих коэффициентов заключается в применении теоремы Планшереля. Легко проверить, что каждая отсчётная функция в пределах отрезка имеет спектральную плотность, равную.

Тогда, если - спектр излучаемого сигналаS(t), то по теореме Планшереля ,

Тогда:

(3.15)

Величина в фигурных скобках есть не что иное, как , т.е. мгновенное значение сигналаS(t) в каждой отсчётной точке (по аналогии с)

Таким образом:

(3.16)

Откуда следует выражение ряда Котельникова:

(3.17)

Теорему Котельникова принято формулировать так: произвольный сигнал, спектр которого не содержит частот выше Гц, может быть полностью восстановлен, если известны отсчётные значения этого сигнала, взятые через равные промежутки временис.

Важная особенность теоремы Котельникова состоит в её конструктивном характере: она не только указывает на возможность разложения сигнала в соответствующий ряд, но и определяет способ восстановления непрерывного сигнала, заданного своими отсчётными значениями.

Теорема Котельникова показывает возможность «цифровизации» непрерывных сообщений.

3.3. Узкополосные сигналы

Сигнал называется узкополосным, если его спектральная плотность отлична от нуля лишь в пределах частотных интервалов шириной П, образующих окрестности точек , причём должно выполняться условие.

Как правило, можно считать, что частота , называемая опорной частотой сигнала, совпадает с центральной частотой спектра.

(3.18)

Обе входящие функции иявляется низкочастотными, их относительное изменение за период высокочастотных колебанийдостаточно малы. Функциюпринято называть синфазной амплитудой узкополосного сигналапри заданном значении опорной частоты, а функцию- его квадратурной амплитудой.

Синфазную и квадратурную амплитуду можно выделить аппаратурным способом. Пусть имеется перемножающее устройство, на один из входов которого подан узкополосный сигнал , а на другой – вспомогательное колебание, изменяющееся во времени по закону. На выходе перемножителя будет получен сигнал:

Пропустим выходной сигнал перемножителя через фильтр нижних частот (ФНЧ), подавляющий составляющие с частотами порядка . Ясно, что с выхода фильтра будет поступать низкочастотное колебание, пропорциональное синфазной амплитуде.

Если на один из входов перемножителя подать вспомогательное колебание , то такая система будет выделять из узкополосного сигналаS(t) его квадратурную амплитуду .

С физической точки зрения узкополосные сигналы представляют собой квазигармонические колебания. Обобщим метод комплексных амплитуд, известный из электротехники на узкополосные сигналы вида (3.18).

Введём комплексную низкочастотную функцию:

(3.19)

называемую комплексной огибающей узкополосного сигнала.

Формулу (3.19), определяющую комплексную огибающую, можно представить также в показательной форме:

(3.20)

Здесь - вещественная неотрицательная функция времени, называемая физической огибающей (часто для практики просто огибающей), - медленно изменяющаяся во времени начальная фаза узкополосного сигнала.

Величины , связаны с синфазной и квадратурной амплитудами соотношениями:

(3.21) Откуда вытекает ещё одна форма записи математической модели узкополосного сигнала:

(3.22)

Введём полную фазу узкополосного колебания и определим мгновенную частоту сигнала, равную производной по времени от полной фазы:

(3.23)

В соответствии с формулой (3.22) узкополосный сигнал общего вида представляет собой колебание, получающееся при одновременной модуляции несущего гармонического сигнала, как по амплитуде, так и по фазовому углу.

Используя равенства (3.21) физическую огибающую можно определить через синфазную и квадратурную амплитуды:

(3.24)

Комплексная огибающая узкополосного сигнала не определяется однозначно сигналом , а зависит также от выбора частоты.

Если обозначить через спектральную плотность комплексной огибающей узкополосного сигналаS(t); который, в свою очередь, имеет спектральную плотность то нетрудно видеть что:

(3.25)

Таким образом, спектральная плотность узкополосного сигнала может быть найдена путём переноса спектра комплексной огибающей из окрестности нулевой частоты в окрестности точек . Амплитуды всех спектральных составляющих сокращаются вдвое; для получения спектра в области отрицательных частот используется операция комплексного сопряжения.

Формула (3.25) полезна тем, что по известному спектру узкополосного сигнала позволяет найти спектр его комплексной огибающей, (которая в свою очередь определяет физическую огибающую и мгновенную частоту сигнала).