1.2.2 Математические модели дискретных каналов связи

В дискретном канале всегда содержится непрерывный канал, а также модем. Последний можно рассматривать как устройство, преобразующее непрерывный канал в дискретный. Поэтому, в принципе можно вывести математическую модель дискретного канала из моделей непрерывного канала и модема. Такой подход часто является плодотворным, однако он приводит к сложным моделям.

Рассмотрим простые модели дискретного канала, при построении которых свойства непрерывного канала и модема не учитывались. Для модели дискретного канала входным и выходным сигналами являются последовательности кодовых символов. Поэтому для определения возможных входных сигналов достаточно указать число m различных символов, из которых формируется последовательность (основание кода), а также длительность передачи каждого символа. Будем считать значение одинаковым для всех символов, что выполняется в большинстве современных каналов. Величина определяется количеством символов, передаваемых в единицу времени. Она называется технической скоростью и измеряется в бодах. Каждый символ, поступивший на вход канала, вызывается появление одного символа на выходе, так что техническая скорость на входе и выходе канала одинакова.

При подаче на вход канала любой заданной последовательности кодовых символов, на выходе появится некоторая реализация случайной последовательности . Кодовые символы обозначим числами от 0 доm-1.

Введем еще одно определение. Будем называть вектором ошибки поразрядную разность (разумеется, по модулю m) между принятой и переданной кодовыми последовательностями (векторами)). Это значит, что прохождение дискретного сигнала через канал можно рассматривать как сложение входного вектора с вектором ошибки. Вектор ошибки играет в дискретном канале примерно ту же роль, что и помеха в непрерывном канале. Таким образом, для любой модели дискретного канала можно записать, пользуясь сложением в векторном пространстве (поразрядным, по модулю m):

(1.4)

где и - случайные последовательности из n символов на входе и выходе канала; -случайный вектор ошибки. Различные модели отличаются распределением вероятностей вектора . Смысл вектора ошибки особенно прост в случае двоичных каналов (m=2), тогда его компоненты принимают значение 0 и 1. Всякая единица в векторе ошибок означает, что в соответствующем месте передаваемой последовательности символ принят ошибочно, а всякий нуль означает безошибочный приём символа. Число ненулевых символов в векторе ошибок называется его весом.

Перечислим наиболее важные и достаточно простые модели дискретных каналов

1) Симметричный канал без памяти определяется как дискретный канал, в котором каждый переданный кодовый символ может быть принят ошибочно с фиксированной вероятностью p и правильно с вероятностью 1-p, причем в случай ошибки вместо переданного символа в может быть с равной вероятностью принят любой другой символ. Таким образом, вероятность того, что принят символ , если был передан

(1.5)

Термин «без памяти» означает, что вероятность ошибочного приема символа не зависит от предыстории, т.е. от того, какие символы передавались до него и как они были приняты.

Очевидно, что вероятность любого n – мерного вектора ошибки в таком канале

, (1.6)

где -число ненулевых символов в векторе ошибки (вес вектора ошибки). Вероятность того, что произошлокаких угодно ошибок, расположенных как угодно на протяжении последовательности длинноq n, определяется формулой Бернулли:

(1.7)

где -биномиальный коэффициент, равный числу различных сочетаний l ошибок в блоке длиной n.

Эту модель называют также биноминальным каналом. Она удовлетворительно описывает канал, возникающий при определенном выборе модема, если в непрерывном канале, отсутствуют замирания, а аддитивный шум белый (или, по крайней мере, квазибелый). Вероятности переходов показаны в виде графа на рис. а:

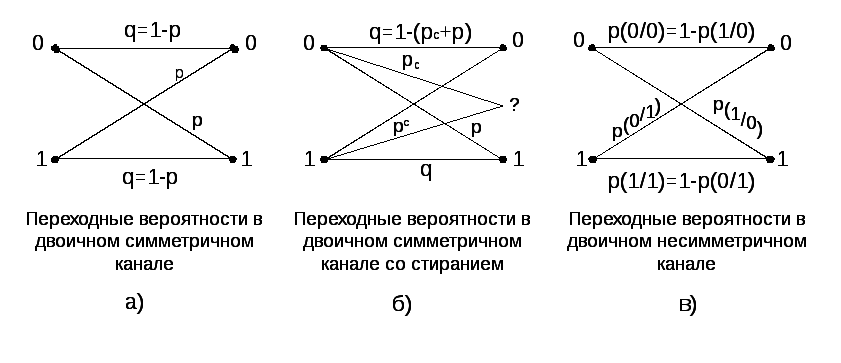
2) симметричный канал без памяти со стиранием отличается от предыдущего тем, что алфавит на выходе канала содержит, дополнительный (m+1)-u символ, обозначаемый знаком «?».

Этот символ появляется тогда, когда 1-я решающая схема (демодулятор) не может надежно опознать переданный символ. Вероятность такого отказа от решения или стирания символа в данной модели постоянна и не зависит от передаваемого символа. За счет введения стирания удается значительно снизить вероятность ошибки, иногда ее даже считают равной нулю. На рис. б) схематически показаны вероятности переходов в такой модели.

3) Несимметричный канал без памяти характеризуется, как и предыдущие модели, тем, что ошибки возникают в нем независимо друг от друга, однако вероятности ошибок зависят от того, какой символ передается. Так, в двоичном несимметричном канале вероятность р (1/0) приема символа «1» при передаче символа «0» не равна вероятности р (0/1) приема «0» при передаче»1» (рис. в)).

4) Марковский канал представляет собой простейшую модель дискретного канала с памятью. В ней вероятность ошибки образует простую цепь Маркова, т.е. зависит от того, правильно или ошибочно принят предыдущий символ, но не зависит от того, какой символ передается. Такой канал, например, возникает, если в непрерывном канале с гауссовским шумом используется ОФМ.

5) Канал с аддитивным дискретным шумом. Является обобщением моделей симметричных каналов. В такой модели вероятность вектора ошибки не зависит от передаваемой последовательности. Вероятность, каждого вектора ошибки считается заданной. Имеется тенденция к тому, что в векторе ошибки единицы расположены близко друг к другу, то есть группированию ошибок.