
- •1.2 Про методологічні основи теорії контролю
- •1.3 Загальні закономірності числового контролю
- •Вхідний поток 1-й вихідний поток 2-й вихідний поток
- •1.4 Про визначення основних понять технічного контролю
- •1.5 Якість контролю
- •1.7 Показники вірогідності вимірювального контролю
- •1.8 Контроль як гарантія якості продукції. Вимоги до точності використовуваних вимірювальних засобів
- •1.9 Середні ризики: терміни, аналіз
- •2 Дослідження середніх ризиків
- •2.1 Вихідних посилок середніх ризків
- •2.2 Дві складові щільності розподілу контрольованого параметра
- •3 Методичний розділ
- •Структура роботі:
- •Джерела посилань
1.7 Показники вірогідності вимірювального контролю
Установлення відповідності показників точності вимірів вимогам вірогідності контролю є однієї з основних задач метрологічної експертизи конструкторської документації [16]. Вірогідність контролю характеризується умовною ймовірністю одержання рішення «не придатний» при контролі параметра, значення якого в дійсності відповідає вимогам технічної документації (вірністю «помилкової відмови» Рл.о.) і умовною ймовірністю одержання рішення «придатний» при контролі параметра, значення якого в дійсності не відповідає вимогам технічної документації (імовірністю «невиявленої відмови» Рн.о).
У
деякій літературі замість «помилкову
відмову застосовують терміни «помилка
першого роду» або «ризик виробника
(постачальника)» і позначають
![]() ,
а замість «невиявлена
відмова»
– «помилка другого роду» або «ризик
споживача (замовника)» і позначають
,
а замість «невиявлена
відмова»
– «помилка другого роду» або «ризик
споживача (замовника)» і позначають
![]() .
.
Коли
контрольований параметр х
і
погрішність виміру
у
розподілені
безупинно в
межах
від
![]() до
до
![]() із щільністю ймовірностей
із щільністю ймовірностей
![]() і
і
![]() значення Рл.о
і
Рн.о,
викликані погрішностями вимірів,
знаходять по відомих
формулах
:
значення Рл.о
і
Рн.о,
викликані погрішностями вимірів,
знаходять по відомих
формулах
:
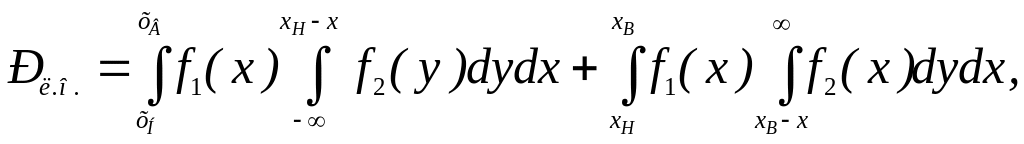 (1.49)
(1.49)
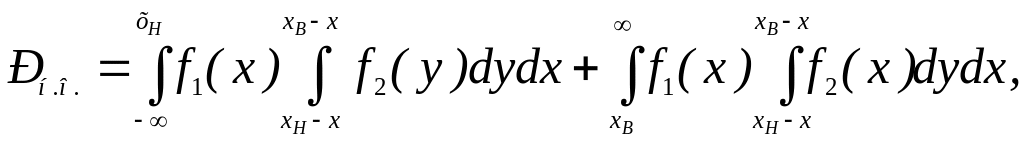 (1.50)
(1.50)
де хн , x – мінімальні й максимальне припустимі значення параметра при контролі.
В
(1.49) і (1.50) перші члени правої частини
являють собою ймовірності «помилкової
(невиявленої) відмови» по нижній границі
допуску, а другі – по верхній границі,
тобто
![]() ,
,
![]() .
.
Практично
контрольовані параметри, як правило,
мають кінцеві розподіли від xmin>-∞
до xmax<∞,
і стандартні апроксимації функцій
розподілу похибок
вимірів
також мають кінцеві розподіли від
![]() до
до
![]() .
Отже,
формули
(1.49) і (1.50) у представленому виді прийнятні
для
рішення практичних задач у названих
умовах,
оскільки
необхідно змінювати межі інтегрування
залежно від співвідношень області
розподілу параметра {х}=[xmin,…,xmax],
його допуску при контролі
.
Отже,
формули
(1.49) і (1.50) у представленому виді прийнятні
для
рішення практичних задач у названих
умовах,
оскільки
необхідно змінювати межі інтегрування
залежно від співвідношень області
розподілу параметра {х}=[xmin,…,xmax],
його допуску при контролі
![]() й
області розподілу похибки виміру
й
області розподілу похибки виміру
![]() .
.
По визначенню результат виміру z=x+y. Найбільший практичний інтерес представляють випадки, коли параметри контрольованих виробів можуть виходити за кожну із двох границь допуску, а погрішність виміру менше допуску на параметр, тобто
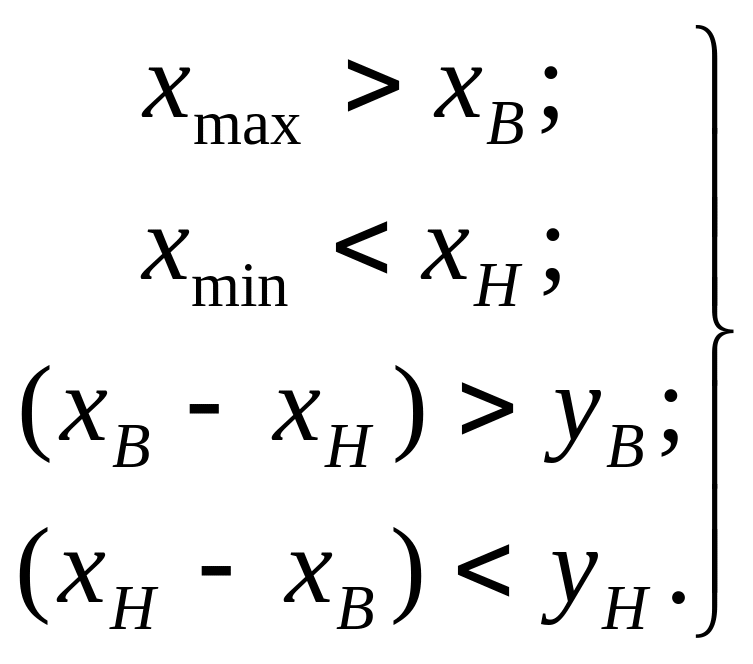 (1.51)
(1.51)
Розподіл f1(x) і f2(y) тут і далі вважаємо безперервними.
З розмірного аналізу треба, що в даних умовах для події «помилкової відмови» по хн, область інтегрування визначається системою нерівностей
![]() (1.52)
(1.52)
а для події «помилкової відмови» по хв — системою нерівностей
![]() (1.53)
(1.53)
При визначенні Рл. про на відміну від (1.49) інтегрування по х повинне вестися тільки по тій частині області розподілу параметра в межах допуску, де можливі «помилкові відмови» при певних співвідношеннях між допуском на параметр і погрішностями вимірів. Так, «помилкові відмови» по хв при умовах (1.52) можливі тільки для тих значень параметра, які відрізняються від хв на величини менше, ніж ув. Якщо ж значення параметра перебувають у межах від хн до (хв-ув), то «помилкові відмови» по хв неможливі при будь-яких значеннях похибок вимірів, і інтегрування по цій ділянці не ведется.
Замінивши в (1.49) межі інтегрування згідно (1.52) і (1.53) і позначивши Рл.о індекс відповідної умови (1.51), одержуємо
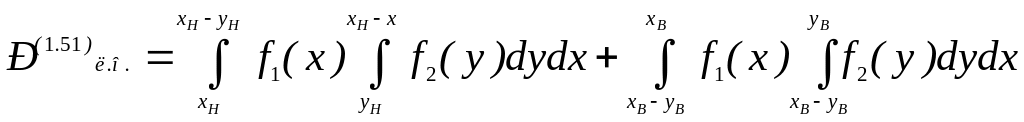 (1.54)
(1.54)
Приклад 1. Нехай контрольований параметр і погрішність виміру мають рівномірні розподіли
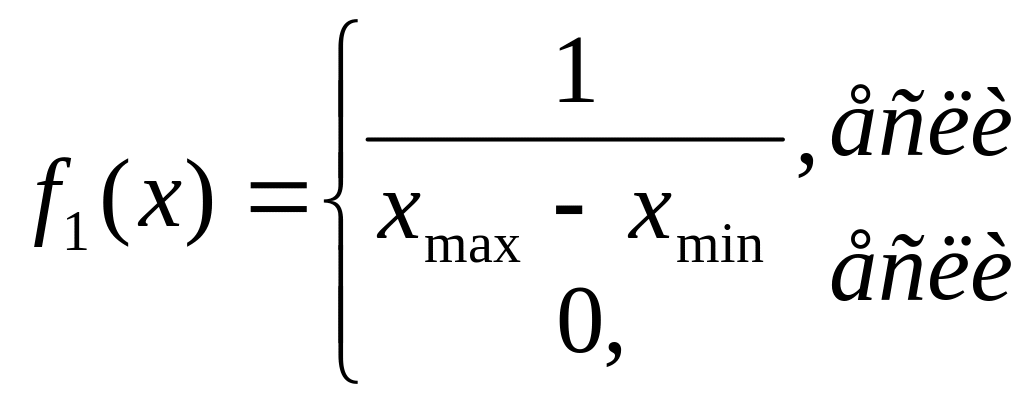
![]() (1.55)
(1.55)
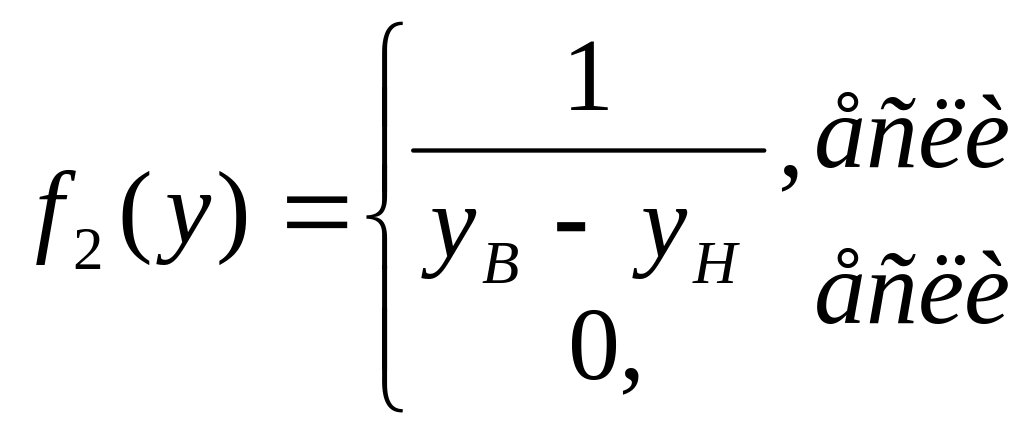
![]() (1.56)
(1.56)
Підставляючи (1.55), (1.56) в (1.54), отримаємо
![]() (1.57)
(1.57)
«Невиявлені
відмови» по хн
можливі при
![]() й тільки при позитивних значеннях
похибок вимірів, що перевищують
й тільки при позитивних значеннях
похибок вимірів, що перевищують
![]() ,
а по
,
а по
![]() - при
- при
![]() й тільки при негативних значеннях
похибок виміру, менших, чим
й тільки при негативних значеннях
похибок виміру, менших, чим
![]() .
.
В умовах
(1.51) для розрахунку як
![]() ,
так й
,
так й
![]() є дві якісно різні ситуації, коли
абсолютне значення похибки виміру менше
абсолютного значення відповідної
величини виходу розміру параметра за
межі допуску й навпаки, тобто
є дві якісно різні ситуації, коли
абсолютне значення похибки виміру менше
абсолютного значення відповідної
величини виходу розміру параметра за
межі допуску й навпаки, тобто
![]() (1.58)
(1.58)
![]() (1.59)
(1.59)
![]() (1.60)
(1.60)
![]() (1.61)
(1.61)
З розмірних співвідношень треба, що для події «невиявленої відмови» по хв при умовах (1.51) і (1.58) область інтегрування визначається системою нерівностей:
![]() (1.62)
(1.62)
а при умовах (1.51) і (1.59) - системою нерівностей:
![]() (1.63)
(1.63)
Аналогічно для події «невиявленої відмови» по хн при умовах (1.50) і (1.59) область інтегрування визначається системою нерівностей:
![]() (1.64)
(1.64)
а при умовах (1.7.3) і (1.7.13) - системою нерівностей:
![]() (1.65)
(1.65)
Замінивши в (1.50) межі інтегрування згідно (1.62) – (1.65) стосовно до конкретних співвідношень (1.58) – (1.61), отримаємо відповідну формулу для визначення Рно. Так, при умовах (1.58) і (1.60)
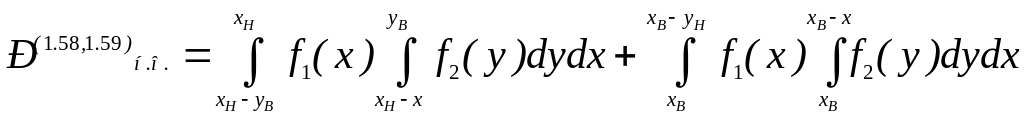 (1.66)
(1.66)
Пі умовах (1.59) і (1.62):
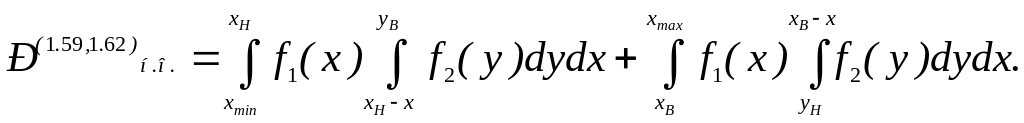
При умовах (1.58) і (1.61)
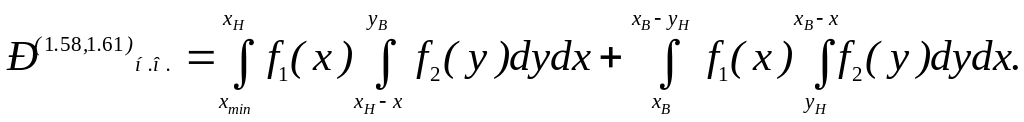
При умовах (1.59) і (1.60)
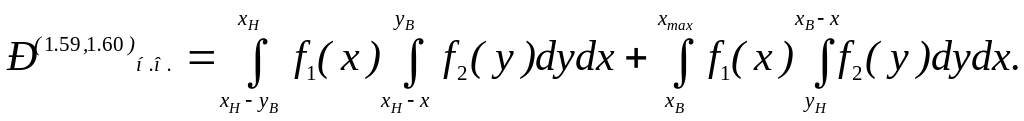
Приклад
2.
Нехай
і
![]() мають вигляд (1.55) і (1.56). Підставляючи
(1.55) і (1.56) в (1.66), находим
мають вигляд (1.55) і (1.56). Підставляючи
(1.55) і (1.56) в (1.66), находим
![]() (1.67)
(1.67)
тобто
одержали ту ж формулу, що й (1.57). При
![]() формули
(1.57) і (1.67) приймаю
формули
(1.57) і (1.67) приймаю
![]()
Отримані результати дозволяють обчислювати показники вірогідності вимірювального контролю для кінцевих визначень контрольованих параметрів і похибок вимірів [17].
