
- •Мариуполь, пгту, 2010г
- •Итерационные методы.
- •Обратный ход метода Гаусса.
- •Лекция 7
- •Лекция 8
- •Блок-схема метода бисекций.
- •Типы задач оптимизации.
- •Одномерная оптимизация.
- •Решение одномерных задач.
- •Решение многомерной задачи оптимизации методом покоординатного спуска.
- •Решение задачи Коши разностными методами.
- •18.1 Рисунок - Блок-схема метода Эйлера
Решение многомерной задачи оптимизации методом покоординатного спуска.
Первоначально
выбирается некоторая точка
с координатами
,
как показано на рисунке 16.1 Затем
фиксируются все координаты функции
![]() кроме первой и получаем функцию одной
переменной
:
кроме первой и получаем функцию одной
переменной
:
![]() (16.1)
(16.1)
Решая таким образом
одномерную задачу оптимизации для этой
функции, от точки
переходим к точке
![]()
![]() В ней функция
принимает наименьшее значение по
координате
или первому проектному параметру при
фиксированных остальных координатах.
В этом состоит первый шаг процесса
оптимизации, заключающийся в спуске по
координате
.
В ней функция
принимает наименьшее значение по
координате
или первому проектному параметру при
фиксированных остальных координатах.
В этом состоит первый шаг процесса
оптимизации, заключающийся в спуске по
координате
.
Следующий шаг заключается в фиксировании всех координат, кроме второй:
![]() (16.2)
(16.2)
Снова решая задачу
одномерной оптимизации, находим
наименьшее значение функции при
![]() ,
т.е. в точке
,
т.е. в точке
![]()
![]() Аналогично производится спуск по
координатам
Аналогично производится спуск по
координатам
![]() .
В результате этого получаем
последовательность точек
,
,
…,
.
В результате этого получаем
последовательность точек
,
,
…,
![]() ,
в которых значение целевой функции
составляет монотонно убывающую
последовательность
,
в которых значение целевой функции
составляет монотонно убывающую
последовательность
![]()
Таким образом, метод покоординатного спуска сводит задачу многомерной оптимизации к многократному решению одномерной оптимизации по каждому проектному параметру. Сходимость данного метода зависит от вида функции и выбора начального приближения.
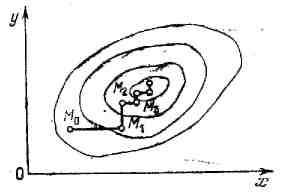
Рисунок 16.1- Пояснение к методу покоординатного спуска
Блок-схема метода покоординатного спуска.
Как показано на
рисунке 16.2 в исходных данных задаются
первоначальные значения всех проектных
параметров и число этих параметров
![]() .
Затем выполняется нахождение целевой
функции при исходных значениях всех
проектных параметров. После чего
определяется минимальное значение
функции по одному параметру при фиксации
всех остальных. Если не достигается
требуемая точность
.
Затем выполняется нахождение целевой
функции при исходных значениях всех
проектных параметров. После чего
определяется минимальное значение
функции по одному параметру при фиксации
всех остальных. Если не достигается
требуемая точность
![]() ,
то вычисления продолжаются.
,
то вычисления продолжаются.
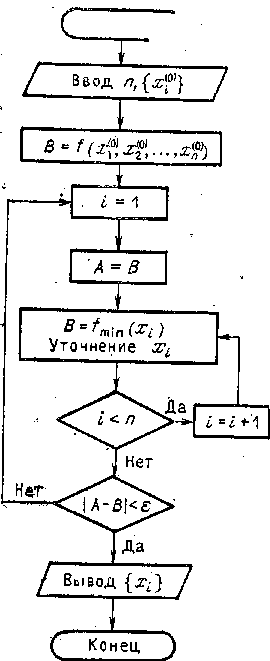
Рисунок 16.2 – Блок- схема метода покоординатного спуска
Лекция 17
Численное дифференцирование.
Аппроксимация производных.
Как известно производной функции называется предел отношения приращения функции к приращению аргумента при стремлении его к нулю:
![]() (17.1)
(17.1)
В численных расчетах на ЭВМ для вычисления производных используют приближенное равенство:
![]() (17.2)
При этом
(17.2)
При этом
![]() и
и
![]() полагают равным некоторому конечному
числу. Поэтому это соотношение (17.2)
называется аппроксимацией производных
с помощью отношения конечных разностей.
полагают равным некоторому конечному
числу. Поэтому это соотношение (17.2)
называется аппроксимацией производных
с помощью отношения конечных разностей.
Дана функция
,
заданная в табличной форме в виде:
![]() и
и
![]() Предположим, что разность между соседними
значениями аргумента постоянна и равна
шагу
Предположим, что разность между соседними
значениями аргумента постоянна и равна
шагу
![]() .
Выражения для вычисления производной
.
Выражения для вычисления производной
![]() при
при
![]() в зависимости от способа нахождения
конечных разностей могут быть следующими:
в зависимости от способа нахождения
конечных разностей могут быть следующими:
![]() ;
;
![]() ;
;
![]() ;
(17.3)
при вычислении
с помощью левых разностей;
;
(17.3)
при вычислении
с помощью левых разностей;
![]() ;
;
;
;
![]() ;
(17.4)
при вычислении с помощью
правых разностей;
;
(17.4)
при вычислении с помощью
правых разностей;
![]() ;
;
![]() ;
;
![]() ;
(17.5) при вычислении
с помощью центральных разностей.
;
(17.5) при вычислении
с помощью центральных разностей.
Используя этот прием можно найти приближенные значения производных любого порядка.
Решение обыкновенных дифференциальных уравнений численными методами.
Понятие решения обыкновенных дифференциальных уравнений (ОДУ).
Многие задачи механики, физики и других отраслей науки и техники
при их математическом моделировании сводятся к дифференциальным уравнениям. В зависимости от числа независимых переменных, дифференциальные уравнения делятся на обыкновенные, содержащие одну независимую переменную, и уравнения с частными производными, содержащие несколько независимых переменных.
Будем рассматривать обыкновенные дифференциальные уравнения, которые в общем виде записываются
![]() ,
(17.6)
,
(17.6)
где
-
независимая переменная,
![]() -
линейная функция,
-
линейная функция,
![]() -
производные от первого до
-
производные от первого до
![]() порядка.
порядка.
Решением
дифференциального уравнения (17.6)
называется всякая функция
![]() ,
которая после ее подстановки в уравнение
превращает его в тождество. Общее решение
дифференциального уравнения
порядка имеет следующий вид:
,
которая после ее подстановки в уравнение
превращает его в тождество. Общее решение
дифференциального уравнения
порядка имеет следующий вид:
![]() (17.7)
(17.7)
где
![]() -
произвольные постоянные.
-
произвольные постоянные.
Геометрически
общее решение ОДУ описывается бесконечным
семейством интегральных кривых с
параметром
![]() ,
а частному решению соответствует одна
кривая с параметром
.
Для выделения частного решения уравнения
первого порядка достаточно задать
координаты
,
а частному решению соответствует одна
кривая с параметром
.
Для выделения частного решения уравнения
первого порядка достаточно задать
координаты
![]() произвольной точки, т.е. одно дополнительное
условие.
произвольной точки, т.е. одно дополнительное
условие.
Для решения уравнений более высокого порядка надо задать столько дополнительных условий, сколько произвольных постоянных в общем решении, т.е. каков порядок уравнения.
В зависимости от способа задания дополнительных условий для получения частного решения ОДУ выделяют два типа задач:
1. Задачи Коши соответствуют заданию условий в одной точке , которая
называется начальная точка начального условия.
2. Краевые задачи соответствуют заданию условий в более, чем одной точке,
например, в двух
точках
![]() и
и
![]() .
Условия называются граничными или
.
Условия называются граничными или
краевыми.
