Лекция 7

АПРОКСИМАЦИЯ ФУНКЦИИ

.

Понятие о приближении функции

Пусть величина у является функцией аргумента х. Это означает, что любому значе­нию х из области определения поставлено в соответствие значение у. Вместе с тем, на практике часто неизвестна явная связь между у и х, т. е. невозможно записать эту связь в виде некоторой зависимости y = f(x). В некото­рых случаях даже при известной зависимости y = f(x) она настолько громоздка (например, содержит трудно вычисляемые выражения, сложные интегралы и т, п.), что ее использование в практических расчетах затрудни­тельно.

Наиболее распространенным и практически важным случаем, когда вид связи между параметрами χ и у не­известен, является задание этой связи в виде некоторой таблицы (x, у). Это означает, что дискретному множест­ву значений аргумента (x_i) поставлено в соответствие множество значений функции ( у_i ) (і = 0, 1, ..., n). Эти значения — либо результаты расчетов, либо эксперимен­тальные данные. На практике нам могут понадобиться значения величины у и в других точках, отличных от уз­лов (x_i) . Однако получить эти значения можно лишь путем очень сложных расчетов или проведением дорогостоящих экспериментов.

Таким образом, с точки зрения экономии времени и средств мы приходим к необходимости использования имеющихся табличных данных для приближенного вы­числения искомого параметра у при любом значении (из некоторой области) определяющего параметра x, посколь­ку точная связь у = f (х) неизвестна.

Этой цели и служит задача о приближении (аппро­ксимации) функций. Данную функцию f(x) требуется приближенно заменить (аппроксимировать) на некоторую функцию φ(х), так, чтобы отклонение φ (х) от f(x) в заданной области было наимень­шим. Функция φ (х) при этом называется аппроксими­рующей. Для практики весьма важен случай аппроксимации функции многочленом

φ (х) = а₀ + а₁х + а₂х² + ... +а_тх^т (7.1) При этом коэффициенты, будут подби­раться так, чтобы достичь наименьшего отклонения мно­гочлена от данной функции.

Графическое изображение аппроксимации функции приведено на рис.7.1.

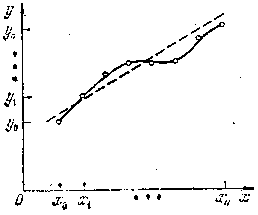
Рисунок 7.1. - Аппроксимация функции.

Точечная аппроксимация. Интерполирование функции.

Если приближение строится па заданном дискретном множестве точек ixj, то аппроксимация называется точечной. К ней относятся интерполирование, среднеквад­ратичное приближение и др. При построении приближе­ния на непрерывном множестве точек (например, на от­резке [а, в]) аппроксимация называется непрерывной (или интегральной).

Одним из основных ти­пов точечной аппроксимации является интерполирование. Оно состоит в следующем: для данной функции у = f (х) строим многочлен, принимающий в заданных точ­ках (x_i), те же значения ( у_i), что и функция φ (х), т. е.

φ (х) = ( у_i), і = 0, 1, ..., п. (7.2)

При этом предполагается, что среди значений x_t нет одинаковых, т. е. х_{ ≠ х_к при і≠ к. Точки (x_i), называются уз­лами интерполяции, а много­член φ (х) — интерполяционным многочленом. Таким образом, близость ин­терполяционного многочлена к заданной функции состоит в том, что их значения совпада­ют на заданной системе точек.