Задание №6.20

Начальные данные:

Случайная величина X задана плотностью вероятности:

Определим сначала константу "c". Для этого воспользуемся условием нормировки:

Поскольку наша функция существует не на всей области, а только в интервале [a,b], то условие нормировки в данном случае записывается так:

Подставим наши начальные данные и найдем константу "c":

Теперь найдем математическое ожидание:

Дисперсия нашей непрерывной величины X равна:

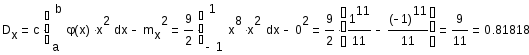
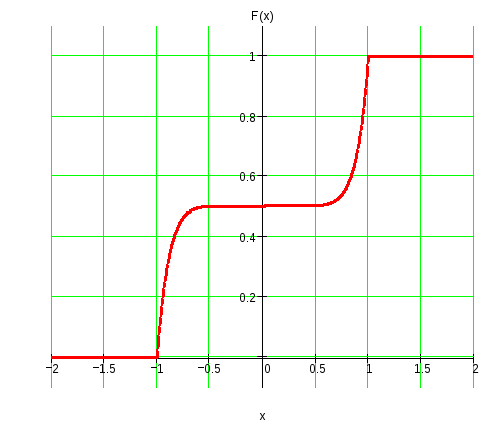
Теперь найдем функцию распределения величины X:

У нас имеется 3 интервала:

1)<-1

2)[-1,1]

3)>1

На первом интервале функция плотности вероятности не существует, поэтому она равна 0, значит и функция распределения на этом интервале тоже равна 0.

На втором интервале функция распределения изменяется по некоторому закону, увеличиваясь от 0 до 1.

На третьем интервале функция распределения не изменяется и остается равной 1.

Осталось найти вероятность попадания величины X в интервал [,]:

Задание №7.20

Начальные данные:

Построим график случайной величины Y=(x):

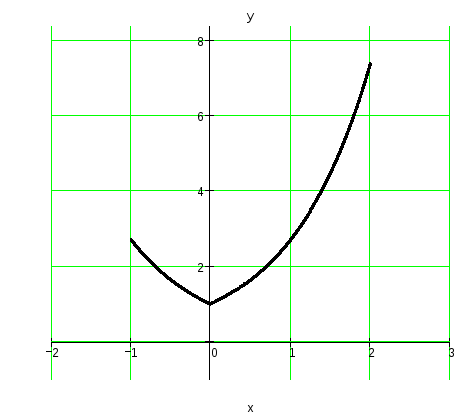
Поскольку величина X равномерно распределена на промежутке [a;b], то ее плотность вероятности равна:

Определим обратные функции Y=(y) на интервале [0;2.718):

Определим обратные функции Y=(y) на интервале [2.178;7.389]:

Плотность вероятности величины y равна:

Задание №8.20

Начальные данные:

Получаем следующую фигуру:

Поскольку двумерная плотность вероятности f(x,y) одинакова для любой точки нашей области и равна константе "c", то найдем данную величину, используя условие нормировки:

Однако стоит учесть то, что это условие нормировки для всей области определения. В нашем случае функция ограничена, поэтому условие нормировки запишется так:

D

, где D - наша область

Найдем недостающий параметр "c":

Для того чтобы высчитать коэффициент корреляции между величинами X и Y, необходимо до этого высчитать их математические ожидания, затем дисперсии, а потом уже и сам коэффициент.

Высчитаем математические ожидания наших величин:

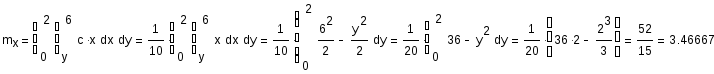
Теперь найдем дисперсии X и Y:

Определяем корреляционный момент:

Теперь найдем необходимый коэффициент корреляции:

Задание №9.20

Исходные данные:

Решение:

Математическое ожидание величины U:

Математическое ожидание величины V:

Дисперсия величины U:

Дисперсия величины V:

Математическое ожидание между величинами U и V:

Корреляционный момент между величинами U и V:

Коэффициент корреляции между величинами U и V:

Математическое ожидание величины x₂²:

Математическое ожидание величины x₁^.x₂:

Математическое ожидание величины x₁^.x₃:

Математическое ожидание величины x₂^.x₃:

Одномерная выборка

Построим вариационный ряд:

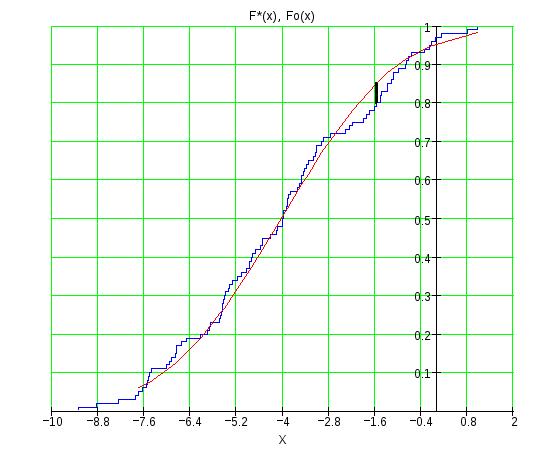
Сделаем таблицу для построения графика эмпирической функции F^*(x), которая определяется формулой:

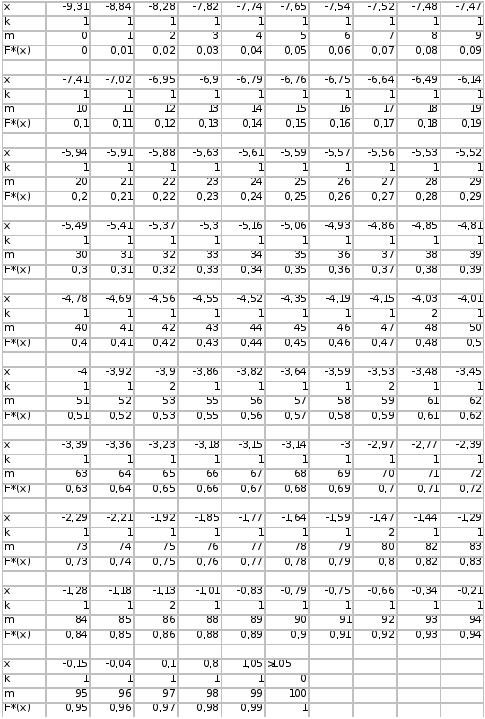
k - количество одинаковых чисел в выборке,

m - номер числа в вариационном ряду

График эмпирической функции представлен в конце задания вместе с графиком гипотетической функции F₀(x).

Определим количество непересекающихся и примыкающих друг к другу M интервалов:

где - количество чисел в выборке

Построим гистограмму равноинтервальным методом:

Определим длину интервала:

Построим гистограмму равновероятностным методом:

Вычислим точечные оценки числовых характеристик:

Состоятельная оценка математического ожидания:

Несмещенная состоятельная оценка дисперсии:

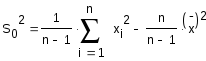
Несмещенная состоятельная оценка среднеквадратического отклонения:

Вычислим интервальные оценки математического ожидания и дисперсии с надежностью =0.95.

Доверительный интервал для математического ожидания:

Согласно центральной предельной теореме при достаточно большом n закон распределения можно считать нормальным, поэтому воспользуемся следующей формулой для случайной величины X с неизвестным законом распределения:

где z_=arg(/2)=arg(0.475)=1.96 - значение аргумента функции Лапласа, тогда интервал равен:

Доверительный интервал для дисперсии:

Выдвинем двухальтернативную гипотезу о законе распределения случайной величины:

Определим оценки неизвестных параметров гипотетического закона распределения:

Проверим гипотезу с помощью критерия ². Вычислим значения критерия ² на основе равноинтервального статистического ряда. Теоретические вероятности попадания случайной величины вычислим по формуле:

Данные для расчета теоретических вероятностей представлены в таблице:

Определим значение критерия ² по формуле:

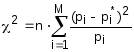
Найдем значения критерия для каждого значения, а затем общий.

Тогда, значение критерия равно:

Определяем число степеней свободы:

k=M-1-s,

где s - число параметров, от которых зависит выбранный гипотезой H₀ закон распределения,

При заданном уровне значимости =0.05 сравним полученное значение критерия ² со значением ²_,k из таблицы распределения ², которое равно:

Поскольку ²<²_,k, то гипотеза H₀ принимается.

Проверим гипотезу с помощью критерия Колмогорова:

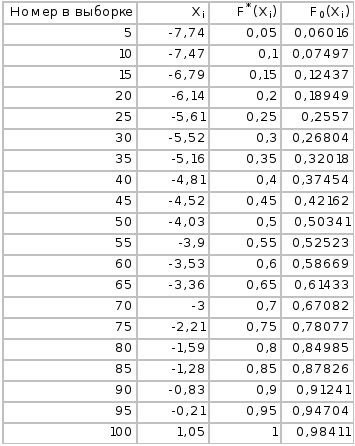
По графику определим максимальное отклонение между функциями F^*(x) и F₀(x):

Определяем значение критерия:

Из таблицы распределения Колмогорова выбираем критическое значение _, где =1-=0.95

_=1.36

Поскольку _, то гипотеза H₀ принимается.

Построим график гипотетической функции F₀(x) совместно с графиком эмпирической функции распределения F^*(x):