
контрольная работа по ТВиМС
.docx
Группа N 902901 Студент N 30
Варианты заданий: ----------------------------------------------------------------
|Номер задания | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 |
--------------------------------------------------------------------
|Номер варианта| 35 | 14 | 29 | 32 | 35 | 34 | 6 | 10 | 30 |
--------------------------------------------------------------------
Одномерная выборка:
1.30 1.01 0.38 3.56 3.90 0.03 6.84 7.75 2.93 4.73 1.39 0.11 0.20 5.72 0.33 2.49
2.49 0.86 5.79 0.77 1.19 4.65 2.52 2.56 1.72 3.77 7.79 1.37 2.51 4.51 6.79 0.16
0.61 2.79 1.74 1.40 2.36 0.14 0.59 1.92 0.82 3.19 5.99 6.53 1.45 0.63 2.73 2.88
0.26
Двумерная выборка:
( 6.65; 2.47) ( 2.28; -1.02) ( -3.06; -2.78) ( 2.60; 1.44) ( -0.80; -1.10)
( 3.69; -1.63) ( 3.56; -2.39) ( 5.79; 4.98) ( -3.75; -6.33) ( -2.33; 0.05)
( -2.12; -5.73) ( -1.22; 3.45) ( 3.47; 4.04) ( 5.45; 3.74) ( -0.63; -0.33)
( 1.02; -0.33) ( -0.84; -0.42) ( -2.28; 2.27) ( 1.56; 3.44) ( 3.41; 2.69)
( 3.32; 0.89) ( -3.14; -5.06) ( 5.92; 3.98) ( -2.64; 0.70) ( 1.28; 0.69)
Контрольная работа №1.
Теория вероятностей
Задача 1.35
В урне 3 белых и 7 черных шаров. Из урны вынимают сразу 6 шаров. Найти вероятность того, что все шесть шаров будут черные.
Пусть А – событие заключающееся в том, что извлечено 6 черных шаров. Всего шаров – 10. Тогда общее число случаев
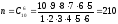
Число благоприятных случаев
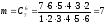
Наконец
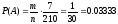
Ответ: вероятность того, что все шесть шаров будут черные равна 0.03333.
Задача 2.14
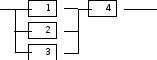
На приведенной ниже схеме соединения элементов, образующих цепь с одним входом и одним выходом. Предполагается, что отказы элементов являются независимыми в совокупности событиями. Отказ любого из элементов приводит к прерыванию сигнала в той ветви цепи, где находится данный элемент. Вероятности отказа элементов 1, 2, 3, 4 соответственно равны p1 = 0.1, p2 = 0.2, p3 = 0.3, p4 = 0.4. Найти вероятность того, что сигнал пройдет со входа на выход.
Пусть событие А
– безотказная работа прибора; Bi
– безотказная работа i-го
элемента; P(Bi)
= qi
– вероятность безотказной работы i-го
элемента;
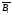 –
отказ i-го
элемента;
–
отказ i-го
элемента;
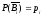 – вероятность отказа i-го
элемента.
– вероятность отказа i-го
элемента.
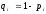 ,
т.к. события
,
т.к. события
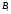 и
и
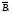 противоположные.
противоположные.
Сигнал пройдет со входа на выход при безотказной работе хотя бы одного из первых трех элементов и безотказной работе четвертого элемента. Это соответствует произведению следующих событий:
A =(B1 + B2 + B3)B4
Так как события совместны и независимы, то удобней переписать это выражение так, чтобы остались только произведения событий, и можно было применить формулу произведения независимых событий:
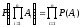
Выражение в скобках равносильно событию, чтобы не отказали все три прибора одновременно, тогда можно записать:
А
=
 и вероятность безотказной работы
прибора:
и вероятность безотказной работы
прибора:
P(A)
= (1 – p1·p2·p3)·
q4
=
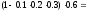 0.5964
0.5964
Ответ: вероятность того, что сигнал пройдет со входа на выход равна 0.5964.
Задача 3.29
Три стрелка производят по одному выстрелу по одной и той же мишени. Вероятность попадания для первого стрелка равна 0.6, для второго – 0.5, для третьего – 0.4. В результате произведенных выстрелов в мишени оказалось две пробоины. Найти вероятность того, что в мишень попал второй стрелок.
Пусть событие Ai – попадание в мишень i-го стрелка, тогда вероятности этих событий: P(A1) = 0.6; P(A2) = 0.5; P(A3) = 0.4. Событие B – в мишени две пробоины. Это событие может наступить только с одним из следующих событий:
С1 – в мишень попали 1-й и 2-й стрелки и непопал 3-й;
С2 – в мишень попали 2-й и 3-й стрелки и непопал 1-й;
С3 – в мишень попали 1-й и 3-й стрелки и непопал 2-й;
События Сi несовместны.
 .
Так как события Аi
независимы, то вероятность произведения
этих событий равна произведению
вероятностей этих событий:
.
Так как события Аi
независимы, то вероятность произведения
этих событий равна произведению
вероятностей этих событий:

Аналогично:
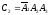
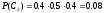
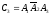
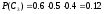
Второй стрелок попадает в мишень в событиях С1 и C2. Событие В наступает совместно со следующими несовместными событиями:
Н1 – в мишень попали 1-й и 2-й стрелки или 2-й и 3-й стрелки, Н1 = С1 + С2;
Н2 – в мишень попали 1-й и 3-й стрелки, Н2 = С3.
В силу несовместности С1 и С2 Р(Н1) = Р(С1) + Р(С2) = 0.18 + 0.08 = 0.26.
Р(Н2) = Р(С3) = 0.12.
Событие В наступает совместно с одним из несовместных событий Hi, поэтому можно применить формулу полной вероятности
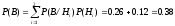 ,
,
где условная вероятность Р(В/Нi) = 1, т.к. при наступлении любого из событий Hi событие В становится достоверным.
Теперь используя формулу Байеса получим вероятность того, что в мишени есть пробоина от второго стрелка, при наличии в мишени двух пробоин:
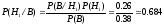
Ответ: вероятность того, что в мишень попал второй стрелок равна 0.684
Задача 4.32
Вероятность появления события А в каждом из 15 независимых опытов равна 0,3. Определить вероятность появления события А семь или восемь раз.
В результате
каждого опыта наступает или не наступает
событие А. Вероятность появления события
Р(А)
= р
= 0.3, следовательно, вероятность не
появления события А:
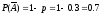 .
Поскольку опыты независимы, то можно
применить формулу Бернулли для определения
вероятности того, что в n
независимых опытах событие А
произойдет ровно k
раз:
.
Поскольку опыты независимы, то можно
применить формулу Бернулли для определения
вероятности того, что в n
независимых опытах событие А
произойдет ровно k
раз:
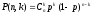
Нас интересует
событие В
= А7
+ А8,
где Аk
– событие заключающееся в том, что А
наступило k
раз. Так как события Аk
несовместны,
то
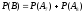 или
или
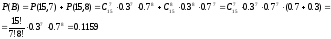
Ответ: вероятность того, что событие А появится семь или восемь раз равна 0.1159.
Задача 5.35
Ряд распределения случайной величины Х представлен таблицей:
|
X |
2 |
3 |
4 |
8 |
10 |
|
P |
0.3 |
* |
0.3 |
0.1 |
0.1 |
Вычислить математическое ожидание и дисперсию величины Х. Рассчитать и построить график функции распределения.
Неизвестную вероятность найдем из условия
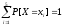
Тогда
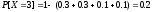
Математическое ожидание:
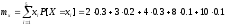 =
4.200
=
4.200
Второй начальный момент:
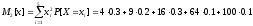 =
24.200
=
24.200
Дисперсия:
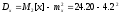 =
6.560
=
6.560
Функция распределения:
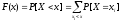 ,
т.е.
,
т.е.
|
X |
x<2 |
x<3 |
x<4 |
x<8 |
x<10 |
x<∞ |
|
F(x) |
0 |
0.3 |
0.5 |
0.8 |
0.9 |
1.0 |
Построим график F(x).

Ответ: mx = 4.2; Dx = 6.56.
Задача 6.34
Случайная величина Х задана плотностью вероятности
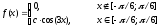
Определить константу с, математическое ожидание, дисперсию, функцию распределения величины Х, а также вероятность ее попадания в интервал [0; 1].
Найдем функцию распределения F(x) и с.
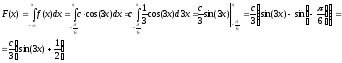
Так как все значения
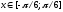 ,
то при
,
то при
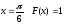 .
Отсюда найдем с.
.
Отсюда найдем с.
 с
= 2
с
= 2
Окончательный вид функции распределения:
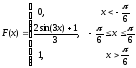
Определим вероятность попадания величины Х на заданный отрезок.
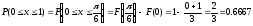
Окончательный вид плотности вероятности:

Математическое ожидание:
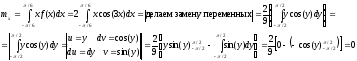
Второй начальный момент:
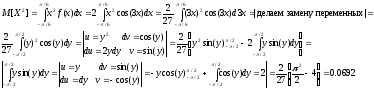
Дисперсия:
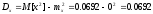
Ответ:
с
= 2; mx
= 0; Dx
= 0.0692;
 .
.
Задача 7.6.
Случайная
величина Х распределена равномерно на
интервале
 .
Построить график случайной величины
.
Построить график случайной величины
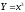 и определить плотность вероятности
g(y).
и определить плотность вероятности
g(y).
Решение:
Так
как Х равномерно распределена в интервале
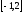 ,
то ее плотность вероятности равна:
,
то ее плотность вероятности равна:
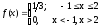
Построим
график величины
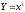 для
x
в интервале
для
x
в интервале
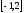 и в зависимости от числа k
обратных функций выделим следующие
интервалы для Y:
и в зависимости от числа k
обратных функций выделим следующие
интервалы для Y:
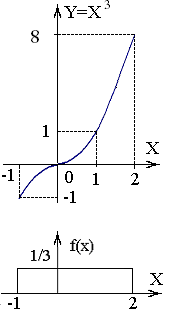
[-, -1[ k = 0,
]-1; 8] k = 1,
]8, +] k = 0.
Так как на интервалах [-, -1[ и ]8, +] обратная функция не существует, то для этих интервалов g(y)=0.В интервале [-1,8] одна обратная функции:
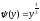
Плотность
вероятности
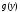 величины Y
определяем по формуле:
величины Y
определяем по формуле:
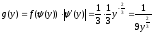
Таким образом, плотность вероятности величины Y равна
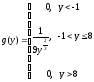
Ответ:

Задача 8.10.
Двумерный случайный вектор (Х, У) равномерно распределен внутри выделенной жирными прямыми линиями на рис. области B. Двумерная плотность вероятности f(x,y) одинакова для любой точки этой области B:

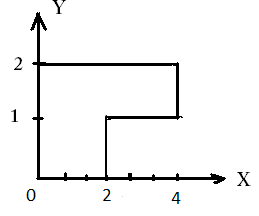
Вычислить коэффициент корреляции между величинами X и Y.
Решение:
Запишем в аналитической форме совместную плотность вероятности:
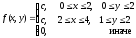
Определим c, используя условие нормировки:
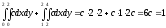
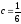
Найдем математическое ожидание и дисперсию величины X:
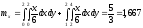
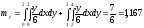
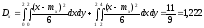
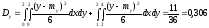
Определим
корреляционный момент
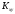 по
формуле:
по
формуле:

Коэффициент корреляции величин X и Y будет равен:
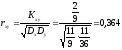
Ответ:

Задача 9.30.
Вычислить
математическое ожидание и дисперсию
величин U
и V,
а также определить их коэффициент
корреляции
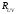 :
:
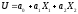
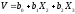
a0=1 b0=6 m1=5 D1=9 K12=1,5
a1=-8 b1=8 m2=-2 D2=1 K23=0
a2=2 b2=6 m3=6 D3=2,5 K13=7,5
Решение:
Определим
коэффициент корреляции
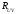 величин U
и V:
величин U
и V:
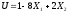

Вычислим математическое ожидание U и V:
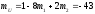
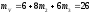
Вычислим
дисперсии
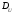 и
и
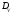 :
:

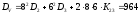
Рассчитаем
корреляционный момент
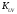 .
.
Для
этого определим
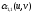 :
:
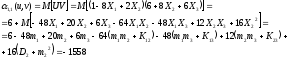
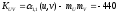
Определим
величину коэффициента корреляции
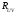 :
:
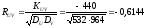
Ответ:

Контрольная работа №2.
Математическая статистика
Задача 10
Дана выборка одномерной, случайной величины Х:
X =[1.30; 1.01; 0.38; 3.56; 3.90; 0.03; 6.84; 7.75; 2.93; 4.73;
1.39; 0.11; 0.20; 5.72; 0.33; 2.49; 2.49; 0.86; 5.79; 0.77;
1.19; 4.65; 2.52; 2.56; 1.72; 3.77; 7.79; 1.37; 2.51; 4.51;
6.79; 0.16; 0.61; 2.79; 1.74; 1.40; 2.36; 0.14; 0.59; 1.92;
0.82; 3.19; 5.99; 6.53; 1.45; 0.63; 2.73; 2.88; 0.26];
Вариационный ряд получается путем расположения элементов выборки по возрастанию:
ВАРИАЦИОННЫЙ РЯД (расположение по строкам)
0.030 0.110 0.140 0.160 0.200 0.260 0.330 0.380 0.590 0.610
0.630 0.770 0.820 0.860 1.010 1.190 1.300 1.370 1.390 1.400
1.450 1.720 1.740 1.920 2.360 2.490 2.490 2.510 2.520 2.560
2.730 2.790 2.880 2.930 3.190 3.560 3.770 3.900 4.510 4.650
4.730 5.720 5.790 5.990 6.530 6.790 6.840 7.750 7.790
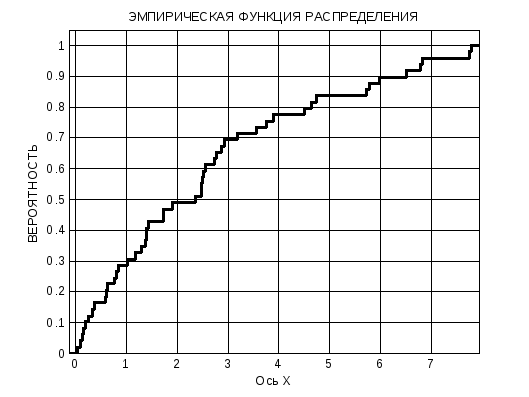
Эмпирическая функция распределения:
Эмпирическая функция распределения случайной величины Х равна частоте того, что Х примет значение меньшее, чем аргумент функции х, и определяется формулой
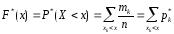
где n – объем выборки, в нашей задаче n =100;
xk – отличающиеся элементы вариационного ряда, k = 1,2,3,…,nx, nx ≤ n;
mk – количество значений в вариационном ряду равых xk.
Суммирование ведется по всем xk удовлетворяющим условию xk < x.
Объединим совпадающие элементы вариационного ряда и сформируем таблицу из четырех столбцов: 1-й столбец – неповторяющиеся значения элементов вариационного ряда xk, 2-й столбец – количество таких элементов m, 3-й - их относительные частоты p*, 4-й – соответствующие значения эмпирической функции распределения.
x m p* F*(x)
0.0300 1.0000 0.0204 0.0204
0.1100 1.0000 0.0204 0.0408
0.1400 1.0000 0.0204 0.0612
0.1600 1.0000 0.0204 0.0816
0.2000 1.0000 0.0204 0.1020
0.2600 1.0000 0.0204 0.1224
0.3300 1.0000 0.0204 0.1429
0.3800 1.0000 0.0204 0.1633
0.5900 1.0000 0.0204 0.1837
0.6100 1.0000 0.0204 0.2041
0.6300 1.0000 0.0204 0.2245
0.7700 1.0000 0.0204 0.2449
0.8200 1.0000 0.0204 0.2653
0.8600 1.0000 0.0204 0.2857
1.0100 1.0000 0.0204 0.3061
1.1900 1.0000 0.0204 0.3265
1.3000 1.0000 0.0204 0.3469
1.3700 1.0000 0.0204 0.3673
1.3900 1.0000 0.0204 0.3878
1.4000 1.0000 0.0204 0.4082
1.4500 1.0000 0.0204 0.4286
1.7200 1.0000 0.0204 0.4490
1.7400 1.0000 0.0204 0.4694
1.9200 1.0000 0.0204 0.4898
2.3600 1.0000 0.0204 0.5102
2.4900 2.0000 0.0408 0.5510
2.5100 1.0000 0.0204 0.5714
2.5200 1.0000 0.0204 0.5918
2.5600 1.0000 0.0204 0.6122
2.7300 1.0000 0.0204 0.6327
2.7900 1.0000 0.0204 0.6531
2.8800 1.0000 0.0204 0.6735
2.9300 1.0000 0.0204 0.6939
3.1900 1.0000 0.0204 0.7143
3.5600 1.0000 0.0204 0.7347
3.7700 1.0000 0.0204 0.7551
3.9000 1.0000 0.0204 0.7755
4.5100 1.0000 0.0204 0.7959
4.6500 1.0000 0.0204 0.8163
4.7300 1.0000 0.0204 0.8367
5.7200 1.0000 0.0204 0.8571
5.7900 1.0000 0.0204 0.8776
5.9900 1.0000 0.0204 0.8980
6.5300 1.0000 0.0204 0.9184
6.7900 1.0000 0.0204 0.9388
6.8400 1.0000 0.0204 0.9592
7.7500 1.0000 0.0204 0.9796
7.7900 1.0000 0.0204 1.0000
График F*(x) см. ниже.
Построение гистограмм
а) Равноинтервальный метод
В этом методе диапазон значений вариационного ряда делится на равные интервалы и подсчитывается число mi точек, попавших на каждый интервал. Точки подсчитываются по вариационному ряду или по таблице для построения эмпирической функции распределения. Если значение точки попадает на границу между интервалами, то в счетчик каждого интервала добавляется по 0.5.
Число интервалов гистограммы определяется по формуле:
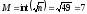
Все интервалы имеют равную длину, следовательно:
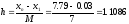
ТАБЛИЦА ДЛЯ ПОСТРОЕНИЯ ГИСТОГРАММЫ
инт 1 2 3 4 5 6 7
mi 15.0000 9.0000 11.0000 3.0000 3.0000 4.0000 4.0000
fi 0.2761 0.1657 0.2025 0.0552 0.0552 0.0736 0.0736
Ai 0.0300 1.1386 2.2471 3.3557 4.4643 5.5729 6.6814
Bi 1.1386 2.2471 3.3557 4.4643 5.5729 6.6814 7.7900
Здесь инт – номер интервала гистограммы;
mi – количество значений вариацонного ряда, попавших в i-ый интервал;
fi
– статистическая плотность (высота)
i-го
интервала равная
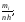
Ai – левая граница i-го интервала гистограммы;
Bi – правая граница i-го интервала гистограммы;
Начинается
гистограмма с точки х
= 0.0300
и заканчивается при х
=7.7900
(первая и последняя
точки вариационного ряда). Площадь
каждого столбика гистограммы равна
относительной частоте
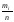 .
.
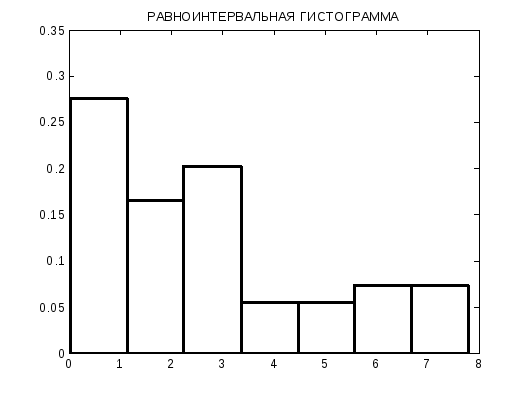
б) Равновероятностная гистограмма
При построении гистограммы этим методом интервалы определяются так, чтобы на каждый из них попало бы одинаковое число точек, т.е. вариационный ряд делится по порядку на М равных групп. Если значение последнего элемента интервала совпадает со значением первого элемента следующего интервала, то это значение берется в качестве границы между этими интервалами. Если такие значения не совпадают, то в качестве границы берется средняя точка между ними.
ТАБЛИЦА ДЛЯ ПОСТРОЕНИЯ ГИСТОГРАММЫ
i Ai Bi hi fi
1.0000 0.0300 0.3550 0.3250 0.3077
2.0000 0.3550 0.9350 0.5800 0.1724
3.0000 0.9350 1.5850 0.6500 0.1538
4.0000 1.5850 2.5150 0.9300 0.1075
5.0000 2.5150 3.3750 0.8600 0.1163
6.0000 3.3750 5.7550 2.3800 0.0420
7.0000 5.7550 7.7900 2.0350 0.0491
Здесь: i – номер интервала гистограммы;
Ai – левая граница i-го интервала гистограммы;
Bi – правая граница i-го интервала гистограммы;
hi – ширина i-го интервала;
fi
– высота i-го
интервала
 ,
,
m – число точек на i-ом интервале;
n – число элементов вариационного ряда.
Гистограмму см. ниже.

Оценка математического ожидания
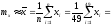 2.6153
2.6153
Оценка дисперсии
Выборочная
дисперсия
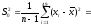 4.8825
4.8825
Среднеквадратическое отклонение S0 = 2.2096
Доверительные интервалы
Построим
доверительные интервалы математического
ожидания mх
и дисперсии Dx
с доверительной вероятностью р
= 0.95. Согласно центральной предельной
теореме при достаточно большом объеме
выборки n
(n
> 20…50) закон распределения несмещенных
точечных оценок mx
и Dx
можно считать нормальным при любом
законе распределения случайной величины.
Тогда доверительный интервал для
математического ожидания будет
определяться выражением:
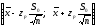 ,
где zp
определяется по таблице нормального
распределения для заданной доверительной
вероятности р.
,
где zp
определяется по таблице нормального
распределения для заданной доверительной
вероятности р.
В нашем
случае n = 49,
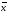 =
2.6153
,
=
2.6153
,
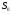 =
2.2096,
zp
= 1.96. Величина
=
2.2096,
zp
= 1.96. Величина
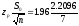 =
0.6187,
а доверительный интервал: (2.6153
±
0.61874
), т.е. (1.9966
< mx
<
3.2340).
=
0.6187,
а доверительный интервал: (2.6153
±
0.61874
), т.е. (1.9966
< mx
<
3.2340).
Доверительный интервал для дисперсии будет определяться выражением:
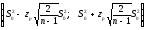 ,
здесь
,
здесь
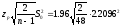 =
1.9534,
а доверительный интервал: (4.8825
±
1.9534),
т.е.(2.9291
< Dx
<
6.8358).
=
1.9534,
а доверительный интервал: (4.8825
±
1.9534),
т.е.(2.9291
< Dx
<
6.8358).
Проверка гипотезы о законе распределения случайной величины
Наблюдая функцию распределения и гистограмму, выдвинем гипотезу H0 об экспоненциальном законе распределения.
Проверка гипотезы по критерию χ2
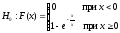
оценка
параметра:
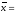 2.6153
(см. выше). Используем равновероятностную
гистограмму. Число интервалов гистограммы
М=7. Относительная частота попадания
значений случайной величины на каждый
интервал одинакова p*
=
2.6153
(см. выше). Используем равновероятностную
гистограмму. Число интервалов гистограммы
М=7. Относительная частота попадания
значений случайной величины на каждый
интервал одинакова p*
=
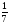 .
Теоретическая вероятность попадания
случайной величины в каждый интервал:
.
Теоретическая вероятность попадания
случайной величины в каждый интервал:

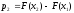
…………………………
 (1)
(1)
…………………………
 ,
,
где xi = xi-1 + h, i= 1,2…7, x0 = 0.
Вероятности Pi для каждого интервала
инт: 1 2 3 4 5 6 7
h: 0.3250 0.5800 0.6500 0.9300 0.8600 2.3800 2.0350
xi: 0.3250 0.9050 1.5550 2.4850 3.3450 5.7250 Inf
exp: 0.1169 0.2925 0.4482 0.6133 0.7217 0.8880 1.0000
pi: 0.1169 0.1757 0.1557 0.1651 0.1084 0.1663 0.1120
здесь: инт – номер интервала;
h – длина интервалов гистограммы;
Inf = ∞;
xi
– значения случайной величины
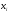 в конце каждого инервала, i
= 1,2,…,7;
в конце каждого инервала, i
= 1,2,…,7;
exp
– значения величин
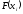 в выражениях (1), i
= 1,2,…,7;
в выражениях (1), i
= 1,2,…,7;
pi – теоретические вероятности попадания случайной величины на i-й интервал, опреде -ляемая формулами (1) , i = 1,2,…,7.
Проверка
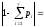 0
<0.01 выполняется.
0
<0.01 выполняется.
Величина
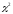 определяется по формуле:
определяется по формуле:
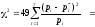 1.898
1.898
число
степеней свободы k
= M
– s
– 1 = 7 – 1 – 1 = 5, здесь s
– число параметров от которых зависит
закон распределения. Для экспоненциального
это один параметр:
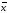 .
По таблице распределения χ2
для уровня значимости α
= 0.05 и k
= 5 имеем: χ2α
=11.07
.
По таблице распределения χ2
для уровня значимости α
= 0.05 и k
= 5 имеем: χ2α
=11.07
Т.к. χ2 < χ2α , то гипотезу H0 принимаем.
Критерий Колмогорова.
Считаем
параметры закона известными, т.е. параметр
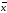 = 2.6153.
Строим теоретическую функцию распределения:
= 2.6153.
Строим теоретическую функцию распределения:
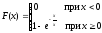 (2)
(2)
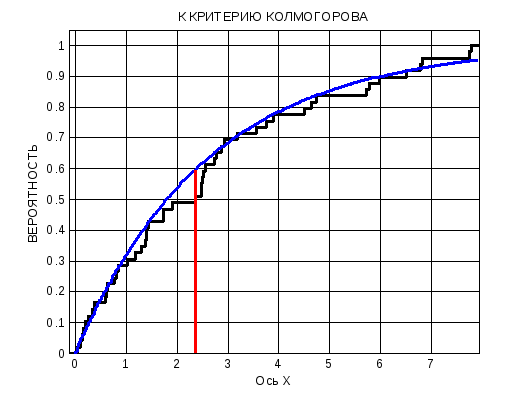
Построим совместно графики эмпирической и теоретической функций распределения (см. ниже).
Найдем
наибольшее отклонение эмпирической
функции F*(x)
от теоретической F(x).
Для этого берем значения х
из таблицы для построения F*(x)
в области самых больших отклонений этих
функций на графике, вычисляем F(x)
для выбранных х
по выражению (2) . Затем вычисляем
наибольшую разницу
 для выбранных х.
для выбранных х.
В нашем случае получим наибольшую разницу в точке х = 2.3600 (штрих-пунктирная линия на графике). Значение функции F*(x) в этой точке (заметим, что если F*(x) лежит ниже F(x), то значение F*(x) надо брать по предыдущей точке)
F*( 2.3600) = 0.4898, а
 =F(2.3600)=1
- exp(-2.3600/2.6153)=
0.5944
=F(2.3600)=1
- exp(-2.3600/2.6153)=
0.5944
Наибольшее отклонение:
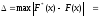 0.10465
0.10465
Тогда значение критерия Колмогорова будет:
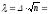 0.1046
∙7 =
0.732
0.1046
∙7 =
0.732
По таблице Колмогорова для уровня значимости α = 0.05 находим λγ = 1.34
Т.к. λ < λγ, гипотезу H0 принимаем.
Оба критерия показывают, что гипотеза об экспоненциальном законе распределения не противоречит опытным данным.
Задача 11
Дана выборка двумерной случайной величины:
B=[6.65 2.47; 2.28 -1.02; -3.06 -2.78; 2.60 1.44; -0.80 -1.10
3.69 -1.63; 3.56 -2.39; 5.79 4.98; -3.75 -6.33; -2.33 0.05
-2.12 -5.73; -1.22 3.45; 3.47 4.04; 5.45 3.74; -0.63 -0.33
1.02 -0.33; -0.84 -0.42; -2.28 2.27; 1.56 3.44; 3.41 2.69
3.32 0.89; -3.14 -5.06; 5.92 3.98; -2.64 0.70; 1.28 0.69];
Здесь символом ";" отделены пары значений случайной величины – это строки, т.е. матрица В имеет два столбца. Обозначим 1-й столбец Х, 2-й – Y, а конкретные i-ые значения случайной величины обозначим (xi,yi).
Число опытов n = 25.
Оценки математических ожиданий по каждой переменной
 1.0876
,
1.0876
,
 0.3084
0.3084
Оценки начальных моментов второго порядка по каждой переменной
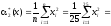 11.1662
,
11.1662
,
 9.3703
9.3703
Оценка смешанного начального момента второго порядка
 6.3412
6.3412
ТАБЛИЦА ДАННЫХ
x y x^2 y^2 x*y
1.0000 6.6500 2.4700 44.2225 6.1009 16.4255
2.0000 2.2800 -1.0200 5.1984 1.0404 -2.3256
3.0000 -3.0600 -2.7800 9.3636 7.7284 8.5068
4.0000 2.6000 1.4400 6.7600 2.0736 3.7440
