БЕЛОРУССКИЙ ГОСУДАРСТВЕННЫЙ УНИВЕРСИТЕТ ИНФОРМАТИКИ

И РАДИОЭЛЕКТРОННИКИ

Факультет непрерывного и дистанционного обучения

Специальность: Программное обеспечение информационных технологий.

Контрольная работа

по дисциплине «Теория вероятностей и математическая статистика»

Выполнил: студент гр.701022 Пугач В.И.(ЗК №-701022-13)

Минск 2009

ЗАДАЧА 1.20.

Из колоды в 36 карт (6, 7, 8, 9, 10, В, Д, К, Т) наугад извлекаются три карты. Определить вероятность того, что будут вытащены карты одной масти.

РЕШЕНИЕ:

Число способов выбрать 4 карты из 36 равно числу сочетаний из 36 по 4 (неупорядоченная выборка без повторений):

;

Число способов, которыми можно выбрать 4 карты из 9 для каждой масти равно числу сочетаний из 9 по 4:

;

Т.к. в колоде 4 различных масти то число способов выбрать 4 карты одинаковой масти равно 4*;

Искомая вероятность будет:

ЗАДАЧА 2.27.

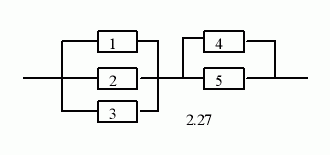
На рисунке 2.1 приведена схема соединения элементов, образующая цепь с одним входом и одним выходом. Предполагается, что отказы элементов являются независимыми в совокупности событиями. Отказ любого из элементов приводит к прерыванию сигнала в той ветви цепи, где находится данный элемент. Вероятности отказа элементов 1, 2, 3, 4, 5 соответственно равны p1=0,1; p2=0,2; p3=0,3; p4=0,4; p5=0,5 . Найти вероятность того, что сигнал пройдет со входа на выход.

РЕШЕНИЕ:

Представим данную схему как цепь, состоящую из двух последовательно соединенных элементов. Каждый из которых, в свою очередь, состоит, соответственно, из трех и двух параллельно соединенных элементов.

Обозначим безотказную работу цепи – В. Тогда

В=В₁*В₂;

для последовательно соединенных элементов, где В₁ и В­₂–вероятности безотказной работы, соответственно, первой и второй полуцепей.

В₁=1– p₁* p₂* p₃;

В₂=1– p₄* p₅;

где p_i – вероятность безотказной работы i-го элемента.

Тогда:

В₁=1–0,1*0,2*0,3=0,994;

В₂=1–0,4*0,5=0,8;

В=0,994*0,8=0,7952;

Искомая вероятность – 0,7952.

ЗАДАЧА 3.1.

На трех автоматических станках изготавливаются одинаковые детали. Известно, что 30% продукции производится первым станком, 25% - вторым и 45% - третьим. Вероятность изготовления детали, отвечающей стандарту, на первом станке равна 0,99 , на втором - 0,988 и на третьем - 0,98. Изготовленные в течение дня на трех станках нерассортированные детали находятся на складе. Определить вероятность того, что взятая наугад деталь не соответствует стандарту.

РЕШЕНИЕ:

Рассмотрим событие A противоположное рассматриваемому. С ним (деталь соответствует стандарту) связано три гипотезы: H₁=(деталь изготовлена первым станком), H₂=(изготовлена вторым станком ), H₃=(изготовлена третьим станком). Вероятности этих событий определяются из условия задачи: p(H₁)=0,3; p(H₂)=0,25; p(H₃)=0,45. Условные вероятности события A также определяются из условия задачи: p(A/H₁)=0,99; p(A/H₂)=0,988; p(A/H₃)=0,98. Отсюда по формуле полной вероятности следует:

p(A) = 0,3*0,99+0,25*0,988+0,45*0,99 =0,9895 .

Тогда искомая вероятность будет равна : 1–0,9895=0,0105.

ЗАДАЧА 4.24.

Вероятность попадания в мишень при одном выстреле равна 0,4. По мишени производится шесть независимых выстрелов. Найти вероятность того, что будет хотя бы пять попаданий в мишень.

РЕШЕНИЕ:

По условию задачи необходимо найти вероятность попадания 5 или 6 выстрелов из 6:

Р=Р(6,5)+Р(6,6);

Находим вероятность промаха для каждого выстрела:

q = 1 –0,4 = 0,6;

Тогда по формуле Бернулли находим:

Искомая вероятность будет равна: Р=0,036864+0,004096=0,04096;

ЗАДАЧА 5.4.

Дискретная случайная величина Х может принимать одно из пяти фиксированных значений 1, 2, 3, 4, 5 с вероятностями 0,3, 0,3, 0,1, 0,1, 0,2 соответственно. Вычислить математическое ожидание и дисперсию величины Х. Рассчитать и построить график функции распределения.

РЕШЕНИЕ:

Находим математическое ожидание:

М[x]=1*0,3+2*0,3+3*0,1+4*0,1+5*0,2=2,6;

D[X] =

=1^2*0,3+2^2*0,3+3^2*0,1+4^2*0,1+5^2*0,2=9;

D[X] =9-2,6^2=2,24;

Функцию распределения определим следующим образом:

x<=1: F(x)=0;

1<x<=2: F(x)=p₁=0,3;

2<x<=3: F(x)=p₁+ p₂=0,3+0,3=0,6;

3<x<=4: F(x)= p₁+ p₂+ p₃=0,6+0,1=0,7;

4<x<=5: F(x)= p₁+ p₂+ p₃+ p₄ =0,7+0,1=0,8;

x>5: F(x)= p₁+ p₂+ p₃+ p₄ +p₅=0,8+0,2=1,0;

Строим график функции распределения(см. рисунок 5.1).

Рисунок 5.1

ЗАДАЧА 6.12.

Случайная величина Х задана плотностью вероятности:

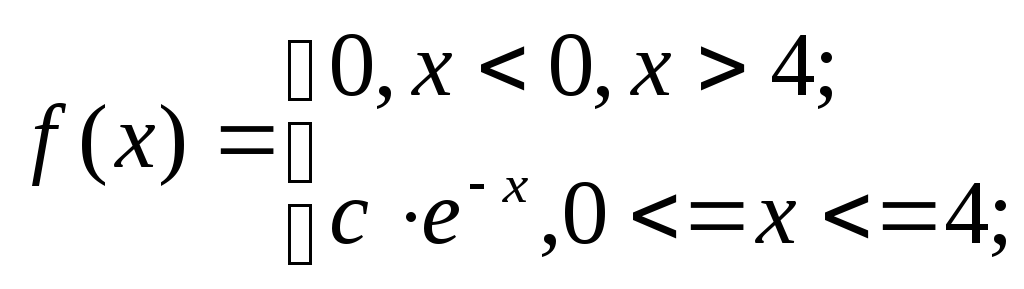
Определить константу С, математическое ожидание, дисперсию, функцию распределения величины Х, а также вероятность ее попадания в интервал[1,2].

РЕШЕНИЕ:

Для нахождения коэффициента с воспользуемся свойством нормировки плотности распределения:

откуда

Находим математическое ожидание:

M[x]= ;

Пусть U=x, =dV, тогда dU=dx, V=-e^-x,

M[x]=

Находим дисперсию:

D_x= α₂(x)-m_x²;

α₂(x)=

Пусть U=x², =dV, тогда dU=2xdx, V=-e^-x,

ранее было получено: тогда:

α₂(x)=

D_x=

Так как плотность вероятности задана различными формулами на разных интервалах, то и функцию распределения будем искать для каждого интервала в отдельности:

для x<0 F(x)=

для 0<=x<=4

для x>4:

Окончательно имеем:

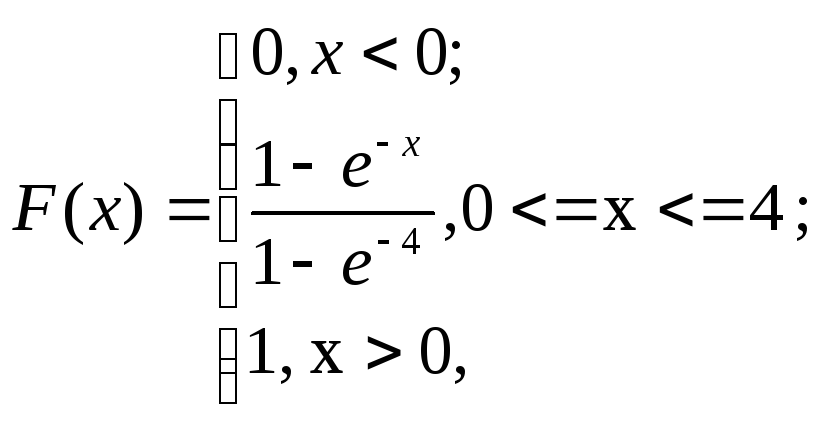
Вероятность попадания величины x интервал[1,2] равен

F(2) –F(1) =

ЗАДАЧА 7.8.

Случайная величина Х распределена равномерно на интервале [-2,1]. Построить график случайной величины Y=x4 и определить плотность вероятности g(y).

РЕШЕНИЕ:

1. Построим график функции Y=X² для x в интервале [-2,1] и определим диапазон значений Y: Y[0; 16] (рис. 7.1).

2. В зависимости от числа k обратных функций выделим следующие интервалы для Y:

(-; 0) k1=0;

[0; 1] k2­­=2;

(1; 16 k2­­=1;

[0; +] k2­­=0;

3. На интервалах [-; 0)и (16; ] обратные функции не существует.

В интервале [0;1] две обратных функции:

ψ₁(y) и ψ₂(y)

Вычислим модули производных обратных функций |ψ’_j (y)|:

|ψ’₁(y)|=

|ψ’₂(y)|=

В интервале (1;16] одна обратная функция ψ₁(y)следовательно, Рис. 7.1.

|ψ’₁(y)|=

4. Так как Х равномерно распределена в интервале -2, 1, то ее плотность вероятности равна:

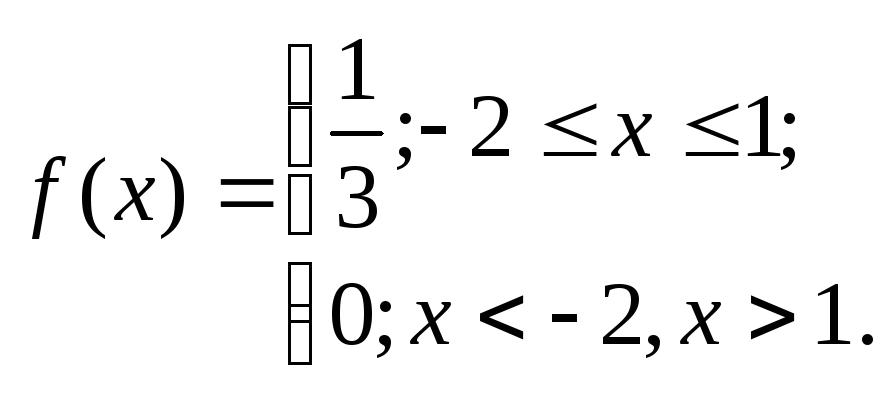
Получаем плотность вероятности величины Y:

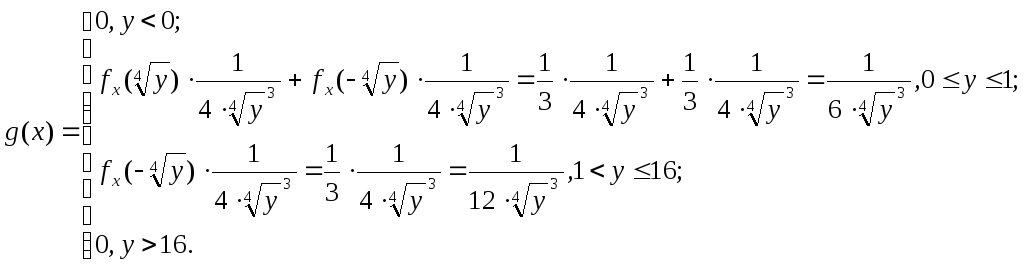
ЗАДАЧА 8.16.

Двухмерный случайный вектор (Х, У) равномерно распределен внутри выделенной жирными прямыми линиями на рис. 8.1 области B. Двухмерная плотность вероятности f(x,y) одинакова для любой точки этой области B:

Вычислить коэффициент корреляции между величинами X и Y.

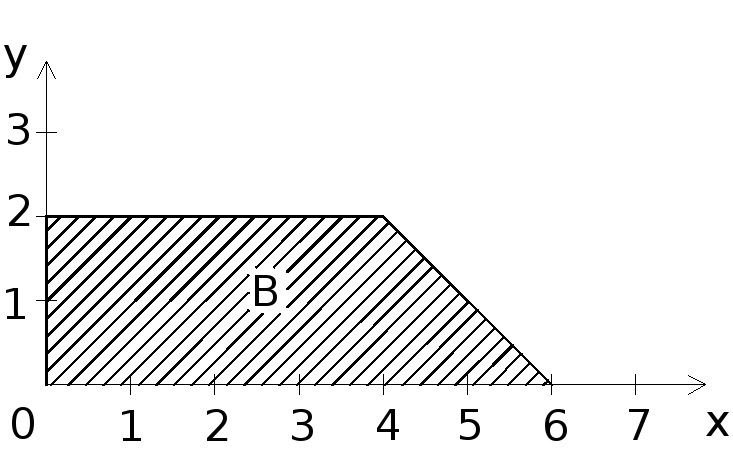
Рисунок 8.1

РЕШЕНИЕ:

Совместная плотность вероятности примет вид

ограниченный поверхностью распределения и плоскостью xOy должен быть

равен единице

Неизвестную константу c определим, используя условие нормировки

плотности вероятности:

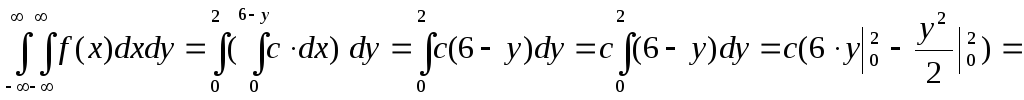
Следовательно c=1/10;

Таким образом

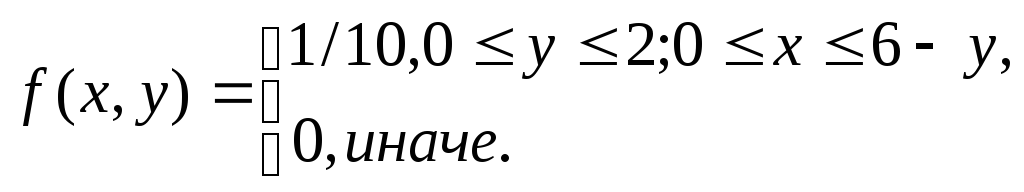
Проверим геометрически полученный результат. Объем тела,

, т.е. объем прямой призмы с основанием в виде прямой трапеции равен:

Вычислим математическое ожидание:

Вычислим дисперсии:

Вычислим корреляционный момент:

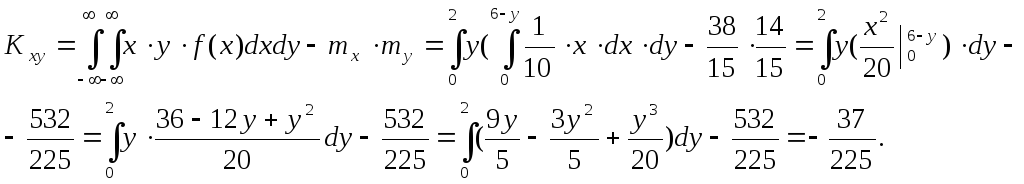После нормировки получаем коэффициент корреляции:

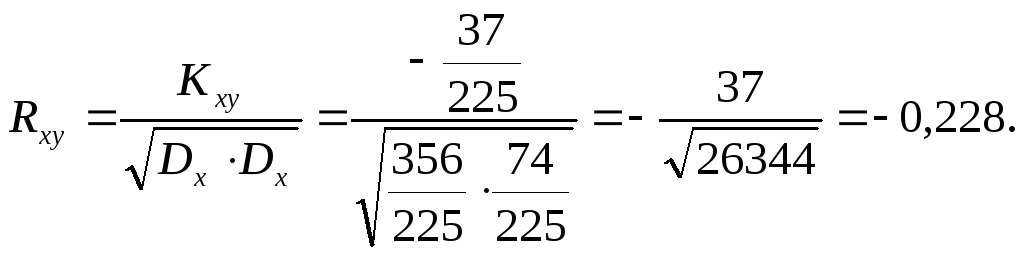
ЗАДАЧА 9.2.

Вычислить математическое ожидание и дисперсию величин

U и V, а так же определить их коэффициент корреляции R_UV:

U= –8+4X­_1­+8X₂;

V=3–4X₂+4X₃;

Величины X₁, X₂ , X₃ имеют следующие числовые характеристики:

m₁=1; m₂=0; m₃=2;

D₁=1; D₂=4; D₃=16;

K₁₂=1; K₂₃=4; K₁₃=2;

РЕШЕНИЕ:

Вычислим математические ожидания U и V:

m_u= –8+4m₁+8m₂ = –8+4*1+8*0 = –4;

m_v= 3–4m₂ + 4m₃=3–4*0+4*2 = 11;

Вычислим дисперсии D_U и D_V:

D_u=4² D₁+8² D₂+2*4*8*K₁₂=16+64*4+64*1=336;

D_v=(-4)² D₂+4² D₃+2*(-4)*4* K₂₃=16*4+16*16-32*4=192;

Рассчитаем корреляционный момент K_UV по формуле

K_UV= M[UV] − m_Um_V;

M[UV]=M[(–8+4X­_1­+8X₂)( 3–4X₂+4X₃)]=

=M[–24+56X₂-32X₃+12X₁-16X₁X₂+16X₁X₃-32X₂X₂+24X₂X₃]=

= –24+56m₂–32m₃+12m₁-16M[X₁X₂]+ 16M[X₁X₃]-32M[X₂X₂]+24 M[X₂X₃]=

= –24+56m₂–32m₃+12m₁-16(m₁m₂+K₁₂)+ 16(m₁m₃+K₁₃) –32M(m₂²+D₂)+ +24(m₂m₃+K₂₃) = –24+56*0–32*2+12*1–16(1*0+1)+ 16(1*2+2) –32(0²+4)+ +24(0*2+4) = –60.

Таким образом

K_UV= –60 –(–4)*11= –16;

Определяем величину R_UV:

Задача 10.123.

По выборке одномерной случайной величины:

Одномерная выборка № 123:

-1.37 2.71 -3.31 -1.78 -1.76 -6.43 -4.67 -5.13 -1.72 -4.06

-1.99 -3.58 -2.68 -3.09 -5.42 -2.14 -2.39-2.96 -4.44-10.12

-5.66 -5.78 -4.74 -6.66 -0.54 -4.68 -0.35 -2.33 -0.01 -2.83

-4.82 -0.72 -2.43-10.28 -5.21 -4.43 -4.57 -9.79 -1.68 -2.71

-7.73 -8.11 -0.00 -0.08 -5.46 -2.96 2.59 -7.28 -4.03 -7.54

-0.75 -2.79 -6.24 -7.33 -3.88 -8.15 -6.05 -5.77 1.21 -2.59

-0.93 -9.79 -7.49 -5.21 -3.12 -5.17 -3.80 -6.51 -6.51 -3.66

-5.36 -2.16 -4.90 -6.00 -4.47 -4.43 -1.53 -5.40 -0.12 -0.35

-1.31 -1.24 -4.12 -6.01 -6.32 -0.99 -5.13 -0.10 -9.27 1.45

-4.15 -2.00 -2.62 -3.80 -2.34 -4.30 -4.96 -8.25 -2.15 -6.88

- получить вариационный ряд;

- построить на масштабно-координатной бумаге формата А4 график

эмпирической функции распределения F*(x);

- построить гистограмму равноинтервальным способом;

- построить гистограмму равновероятностным способом;

- вычислить точечные оценки математического ожидания и дисперсии;

- вычислить интервальные оценки математического ожидания и дисперсии

(γ = 0,95);

- выдвинуть гипотезу о законе распределения случайной величины и

проверить ее при помощи критерия согласия χ2 и критерия Колмогорова (α=0,05). График гипотетической функции распределения F0(x) построить

совместно с графиком F*(x) в той же системе координат и на том же листе.

Решение:

Строим вариационный ряд случайной величины, размещая данные выборки в порядке возрастания:

-10,28 -10,12 -9,79 -9,79 -9,27 -8,25 -8,15 -8,11 -7,73 -7,54

-7,49 -7,33 -7,28 -6,88 -6,66 -6,51 -6,51 -6,43 -6,32 -6,24

-6,05 -6,01 -6,00 -5,78 -5,77 -5,66 -5,46 -5,42 -5,4 -5,36

-5,21 -5,21 -5,17 -5,13 -5,13 -4,96 -4,9 -4,82 -4,74 -4,68

-4,67 -4,57 -4,47 -4,44 -4,43 -4,43 -4,3 -4,15 -4,12 -4,06

-4,03 -3,88 -3,8 -3,8 -3,66 -3,58 -3,31 -3,12 -3,09 -2,96

-2,96 -2,83 -2,79 -2,71 -2,68 -2,62 -2,59 -2,43 -2,39 -2,34

-2,33 -2,16 -2,15 -2,14 -2,00 -1,99 -1,78 -1,76 -1,72 -1,68

-1,53 -1,37 -1,31 -1,24 -0,99 -0,93 -0,75 -0,72 -0,54 -0,35

-0,35 -0,12 -0,1 -0,08 -0,01 0 1,21 1,45 2,59 2,71

Строим график эмпирической функции распределения F*(x) (рис. 10.1). Так как F*(x) является неубывающей функцией и все ступеньки графика F*(x)имеют одинаковую величину 1/n, то таблицу значений эмпирической

функции распределения F*(x) можно не вычислять, а построить ее график

непосредственно по и вариационному ряду, начиная с его первого значения.

Z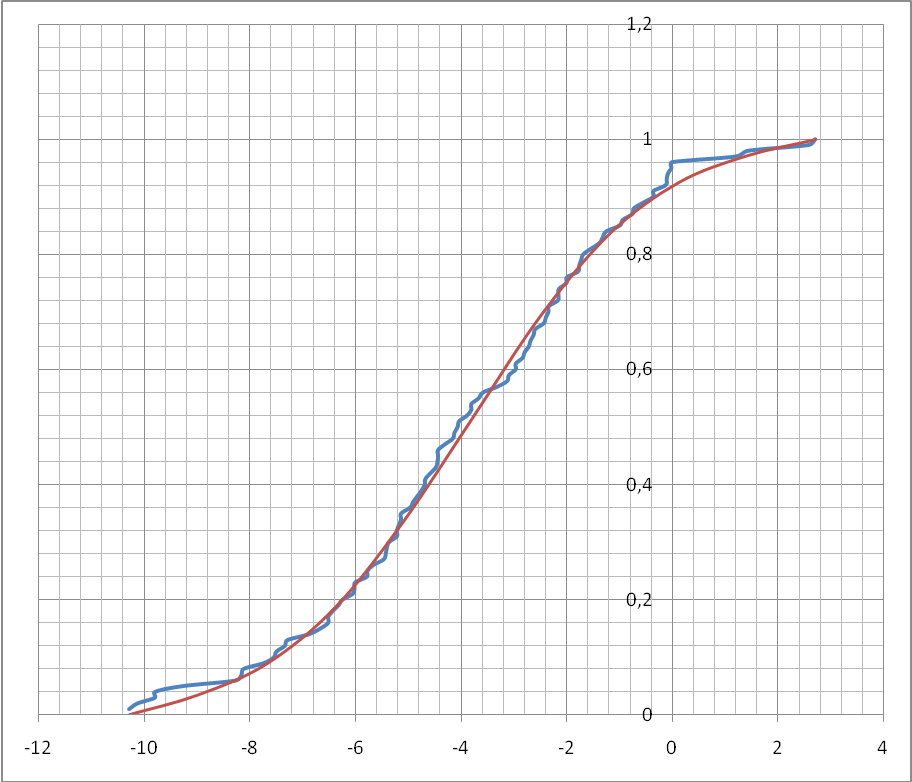

Рисунок 10.1 Графики эмпирической F*(x) (синий) и гипотетической функций

распределения F₀(x) (красный).

Количество интервалов M, необходимое для построения гистограмм,

определим по объему выборки:

;

Для равноинтервальной гистограммы рассчитаем величины hj, Aj, Bj и заполним все колонки интервального статистического ряда (таблица. 10.1):

Таблица 10.1

j	Aj	Bj	hj	vj	pj*	fj*
1	-10,28	-8,981	1,299	5	0,05	0,0385
2	-8,981	-7,682	1,299	4	0,04	0,0308
3	-7,682	-6,383	1,299	9	0,09	0,0693
4	-6,383	-5,084	1,299	17	0,17	0,1309
5	-5,084	-3,785	1,299	19	0,19	0,1463
6	-3,785	-2,486	1,299	13	0,13	0,1001
7	-2,486	-1,187	1,299	17	0,17	0,1309
8	-1,187	0,112	1,299	12	0,12	0,0924
9	0,112	1,411	1,299	1	0,01	0,0077
10	1,411	2,71	1,299	3	0,03	0,0231

Равноинтервальная гистограмма имеет вид, согласно рис. 10.2:

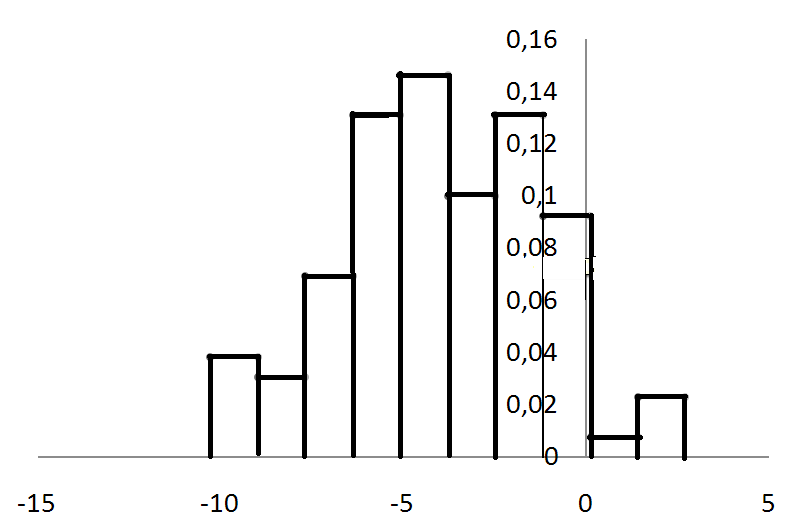
Рисунок10.2. Равноинтервальная гистограмма

Для равновероятностной гистограммы рассчитаем величины ν_j, p_j^*, A_j, B_j, и заполним все колонки интервального статистического ряда (таблица. 10.2):

таблица. 10.2

j	Aj	Bj	hj	vj	pj*	fj*
1	-10,28	-7,515	2,765	10	0,1	0,0362
2	-7,515	-6,145	1,37	10	0,1	0,073
3	-6,145	-5,285	0,86	10	0,1	0,1163
4	-5,285	-4,675	0,61	10	0,1	0,1639
5	-4,675	-4,045	0,63	10	0,1	0,1587
6	-4,045	-2,96	1,085	10	0,1	0,0922
7	-2,96	-2,335	0,625	10	0,1	0,16
8	-2,335	-1,605	0,73	10	0,1	0,137
9	-1,605	-0,35	1,255	10	0,1	0,0797
10	-0,35	2,71	3,06	10	0,1	0,0327

Равновероятностная гистограмма имеет вид, согласно рис. 10.3:

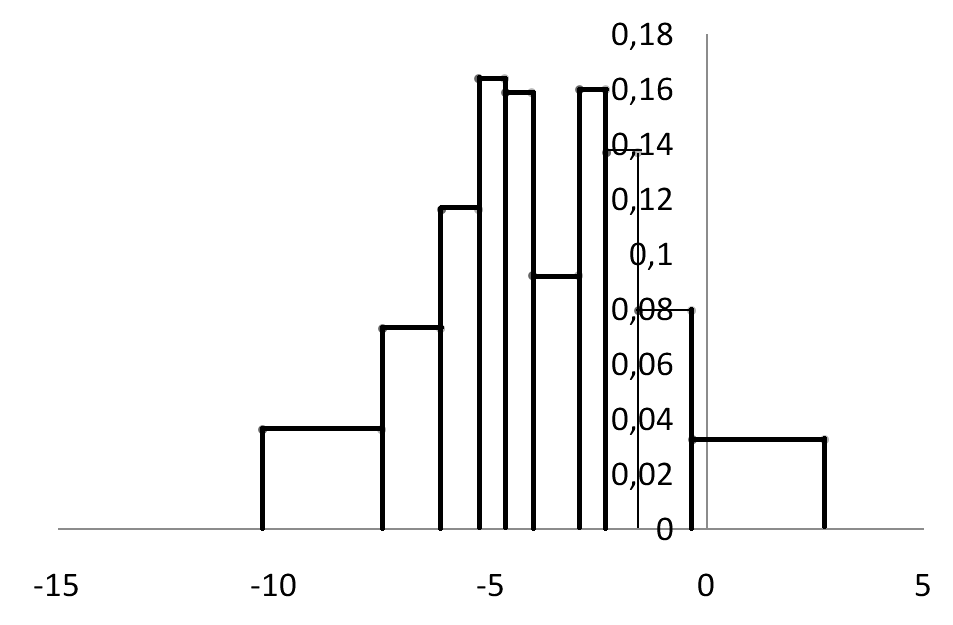
Рисунок10.3. Равновероятностная гистограмма

Вычислим точечную оценку математического ожидания по формуле:

;

Вычислим точечную оценку дисперсии по формуле:

;

Построим доверительный интервал для математического ожидания с надежностью γ = 0,95. Для этого в таблице функции Лапласа найдем значение, равное γ/2= 0,475, и определим значение аргумента, ему соответствующее: z_0,95=argΦ(0,475)=1,96. Затем вычислим

;

и получим доверительный интервал для математического ожидания:

I_0,95(m_x­)=[–4,453; –3,365].

Построим доверительный интервал для дисперсии с надежностью γ = 0,95 по формуле (10.9). Вычислим

;

и получим доверительный интервал для дисперсии:

I_0,95(D_x­)=[5,555; 9,846].

По виду графика эмпирической функции распределения F*(x) и гистограмм выдвигаем двухальтернативную гипотезу о законе распределения случайной величины

H₀ – величина X распределена по нормальному закону:

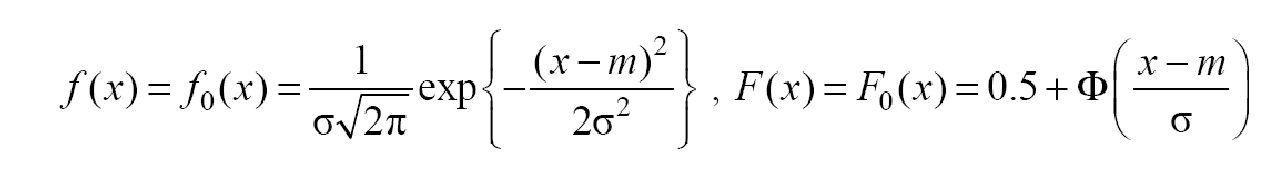
H₁ – величина X не распределена по нормальному закону:

f(x) ≠ f₀(x), F(x) ≠ F₀(x),

Определим оценки неизвестных параметров m и σ гипотетического

(нормального) закона распределения:

m_x^*= –3,9089; σ^*=S₀= = 2,775;

Таким образом, получаем полностью определенную гипотетическую

функцию распределения:

Проверим гипотезу о нормальном законе с помощью критерия

Вычислим значение критерия на основе равноинтервального статистического ряда по формуле:

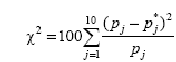
Теоретические вероятности p_i попадания в интервалы равноинтервального статистического ряда нормальной случайной величины с параметрами m^*= –3,9089 ; σ^*=2,775 вычислим по формуле:

Значения функции Лапласа определяем с помощью специальной таблицы. Результаты расчета сводим в таблицу 10.3:

Таблица 10.3

j	Aj	Bj		F0(Aj)	F0(Bj)		pj	pj*	(pj-pj*)^2/pj
1	-∞	-8,981		0	0,034		0,0344	0,05	0,007096
2	-8,981	-7,682		0,0344	0,089		0,0541	0,04	0,003688
3	-7,682	-6,383		0,0885	0,187		0,0982	0,09	0,000689
4	-6,383	-5,084		0,1867	0,337		0,1505	0,17	0,002524
5	-5,084	-3,785		0,3372	0,516		0,1787	0,19	0,000713
6	-3,785	-2,486		0,516	0,695		0,179	0,13	0,013423
7	-2,486	-1,187		0,695	0,836		0,1415	0,17	0,005748
8	-1,187	0,112		0,8365	0,925		0,0886	0,12	0,01112
9	0,112	1,411		0,9251	0,972		0,0469	0,01	0,029001
10	1,411	+∞		0,9719	1		0,0281	0,03	0,000133
Сумма:	1	1	0,074136

Проверяем выполнение контрольного соотношения для p _j :

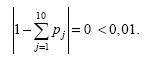
В результате получаем =100*0,074136=7,4136;

Вычислим число степеней свободы по формуле k = M−1−s=10−1−2=7 и по заданному уровню значимости α =0,05 из таблицы распределения χ2 выбираем критическое значение _χα;7²=χ_0,05;7²=14,07.

Так как χ²=7,4136 < χ_0,05;7²=14,07, то гипотена H₀ о нормальном законе распределения принимается (нет оснований ее отклонить).

Проверим гипотезу о нормальном законе с помощью критерия

Колмогорова. Построим график F₀(x) в одной системе координат с графиком

эмпирической функции распределения F^*(x) (см. рис 10.1). В качестве

опорных точек для графика F₀(x)используем 10 значений F₀(Aj) из таблицы.10.3. По графику определим максимальное по модулю отклонение между функциями F^*(x) и F₀(x) (см. рисунок 10.1):

Вычислим значение критерия Колмогорова по формуле:

Из таблицы Колмогорова по заданному уровню значимости α=0,05 выбираем критическое значение λ_γ=λ_1-α=λ_0,95=1,36.

Так как λ=0,4 ≤ λ_0,95=1,36, то гипотезу H₀ о нормальном законе

распределения отвергать нет основания.