Добавил:

inrad Опубликованный материал нарушает ваши авторские права? Сообщите нам.

Вуз:

Белорусский государственный университет информатики и радиоэлектроники

Предмет:

Теория вероятностей и математическая статистика

Файл:

Кр по ТВиМС 4 вариант

.pdf

Скачиваний:

317

Добавлен:

01.04.2014

Размер:

221.31 Кб

Скачать

☆

1 / 21 2 > Следующая >>>

Вариант №4

Задача №1

Собрание, на котором присутствуют 25 человек, в том числе 5 женщин, выбирает делегацию из трех человек. Считая, что каждый из присутствующих с одинаковой вероятностью может быть избран, найти вероятность того, что в делегацию войдут две женщины и один мужчина.

Решение

По условию получаем, что на собрании 5 женщин и 20 мужчин. Событие А – в делегацию вошли две женщины и один мужчина. Найдем количество благоприятных исходов.

n C2	C1	5!	20!	10 20 200
		3!2!	19!1!
5	20

Найдем количество возможных делегаций из 3 человек, которые можно составить из 25 присутствующих.

m C253 2225!!3! 2300

Находим искомую вероятность

P(A) mn 2300200 232 0.087

Ответ: P(A) 0.087.

Задача №2

Гардеробщица выдала одновременно номерки четырем лицам, сдавшим в гардероб свои шляпы. После этого она перепутала все шляпы и повесила их наугад. Найти вероятность того, что ровно три лица получат свои шляпы.

Решение

Событие А1 – первый человек получил свою шляпу; Событие А2 – второй человек получил свою шляпу; Событие А3 – третий человек получил свою шляпу; Событие А4 – четвертый человек получил свою шляпу. Вероятность того что человек получит свою шляпуравна

P(A1) P(A2 ) P(A3) P(A4 ) 14 0.25

Теперь найдем вероятность того, что шляпуполучат ровно три человека:

P(3) P(A1) P(A2 ) P(A3) P(A4 ) P(A1) P(A2 ) P(A3) P(A4 )

P(A1) P(A2 ) P(A3) P(A4 ) P(A1) P(A2 ) P(A3) P(A4 ) 4 0.253 (1 0.25) 0.047

Ответ: P(3) 0.047.

Задача №3

В группе 60 % студентов – юноши. 80 % юношей и 75 % девушек имеют билеты на дискотеку. В группу принесли кем-то потерянный билет. Какова вероятность того, что он принадлежал юноше?

Решение

Событие А – потерянный билет принадлежит кому-то из группы. Это событие уже произошло.

Выдвинем две гипотезы:

H1- билет принадлежит юноше, P(H1) 0.6;

H2 - билет принадлежит девушке, P(H2 ) 0.4. Условные вероятности даны по условию:

P(A/H1) 0.8;P(A/H2 ) 0.75

Значит, полная вероятность будет равна.

P(A) P(H1) P(A/H1) P(H2 ) P(A/H2 ) 0.6 0.8 0.4 0.75 0.78

По формуле Байеса найдем вероятность того, что билет принадлежит юноше

P(H1 / A)	P(H1) P(A/H1)	0.6 0.8	0.615
	P(A)	0.78

Ответ: P(H1 / A) 0.615.

Задача №4

Игральная кость брошена 10 раз. Найти вероятность выпадения единицы не менее

2 раз.

Решение

Событие А – выпадение единицы.

Событие B – единица выпадет не менее двух раз. Вероятность выпадения единицы при броске равна

P(A) 16

Найдем вероятность того, что единица ни разу не выпадет, используем формулу Бернулли P(n,k) Cnk pk (1 p)n k

P(0) C0	P(A)0 P(		10)10	1 1	1	1	10	0.162.
		A
10						6

Найдем вероятность того, что единица выпадет ровно один раз

P(1)	10		9	10	1		1	9	0.323

		P(A) P(A)			6	1	6

Тогда искомая вероятность будет равна

P(B) 1 P(0) P(1) 1 0.162 0.323 0.515 Ответ: P(B) 0.515.

Задача №5

В страховом обществе застраховано 7000 автолюбителей. Размер страхового взноса равен 8 у.е., а в случае аварии страховое общество выплачивает 800 у.е. Какова вероятность что страховое общество к концу года разорится, если вероятность автолюбителю попасть в аварию равна 0,007?

Решение

Найдем максимальное возможное количество, попавших в аварию, автолюбителей, при котором страховое общество еще получит хоть какой-то доход.

Составляем неравенство:

8 7000 800 n 0 n 56000800 70

Значит, еслиn 71, то страховое общество разориться.

Следовательно теперь нам необходимо найти вероятность того что в аварию попадет от 71 до 7000 автолюбителей из 7000.

По условию имеем n 7000, p 0.007,q 0.993,m1 71;m2 7000.

Воспользуемся интегральной теоремой Муавра-Лапласа:

P7000 (71,7000) Ф(x2 ) Ф(x1), где


x	2	m2	np	7000 7000 0.007			996.494;x	m1	np	71 7000 0.007	3.154
x		m2					996.494;x	m1	np		3.154
			npq		7000 0.007 0.993	1			npq	7000 0.007 0.993
			npq		7000 0.007 0.993				npq	7000 0.007 0.993

Таким образом

P7000 (71,7000) Ф(996.494) Ф(3.154)

Определяем:

		1			x	x22
Ф(996.494)		1			e 2		0.5;

		2
		2		0
Ф(3.154)	1		e	x12		0.49919
	1			2
				2
	2
	2

Получаем

P7000 (71,7000) Ф(996.494) Ф(3.154) 0.5 0.49919 8.1 10 4

Ответ: P7000 (71,7000) 8.1 10 4 .

Задача №6

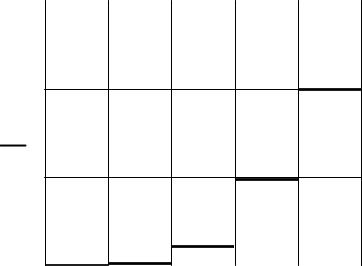
Вероятность сдачи экзамена для каждого из трех студентов равна 0.8. Случайная величина (СВ) Х – число студентов сдавших экзамен. Получить ряд распределения, вычислить функцию распределения F(x) и построить ее график.

Решение

Число студентов сдавших экзамен среди п = 3 случайно отобранных, представляет случайную величину Х с множеством значений X= т = 0, 1, 2, 3, вероятности которых определяются по формуле Бернулли:

		P(X m) Cnm pmqn m , где q 1 p
В нашем случае n =3,			p 0.8, q 1 p 1 0.8 0.2
Вычислим			P(X 0) C30				0,80		0,23	0.008;
			P(X 0) C30				0,80		0,23	0.008;
			P(X 1) C31				0,81	0,22		0.096;
			P(X 2) C32				0,82		0,21	0.384;
			P(X 3) C33				0,83		0,20	0.512.
(Здесь учтено, что C30			= 1, C31 =3, C32 3, C33 = 1)

			xi		0		1		2		3
			pi		0.008	0.096			0.384		0.512

Убеждаемся, что 4 pi				0,008 0,096 0,384 0,512 1
	i 1
Функция распределения F(x):
0;x 0
0.008;0 x 1

	0.096			0.104;1 x			2
F(x) 0.008	0.096			0.104;1 x			2
0.104 0.384 0.488;2 x 3
	0.512 1;x 3
0.488	0.512 1;x 3

1.5
1.5

F(x)

0.5

0
	1	0	1	2	3	4

x	5

Задача №7

Вычислить функцию распределения F(x) и построить ее график. Найти математическое ожидание и дисперсию дискретной случайной величины, заданной рядом распределения

xi	0	2	4	6	8
pi	0,1	0,3	0,2	0,3	0,1

Решение

Математическое ожидание:

M X 5 xi pi 0 0.1 2 0.3 4 0.2 6 0.3 8 0.1 4

i 1

Дисперсия:

D X 5 (xi M X )2 pi 0 4 2 0.1 2 4 2 0.3 (4 4)2 0.2

(6 4)2 0.3 (8 4)2 0.1 5.6

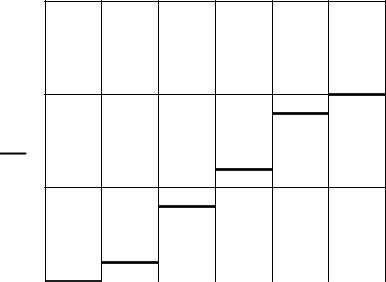
Функция распределения выглядит следующим образом:

0;x 00.1;0 x 2

0.1 0.3 0.4;2 x 4 F(x) 0.4 0.2 0.6,4 x 60.6 0.3 0.9;6 x 8

0.9 0.1 1;x 8

1.5

F(x)

0.5

0
0	2	1	0	1	2	3	4
	2	1	0	1	2	3	4
				x

Задача №8

Плотность вероятности случайной величины Х равна:

0, x 1 f(x)= Cx 2, 1 x 2

0, x>2

Найти постоянную С, функцию распределения F(x), математическое ожидание, дисперсию и вероятность попадания на отрезок [1; 1.5]. Построить графики функций

F(x) и f (x).

Решение

Для нахождения параметра С воспользуемся свойством:

f (x)dx 1

Тогда:

	2					2				2			4C							C						3C
	2					2				2
f (x)dx 1		Cx 2 dx	Cx												4								2					2
f (x)dx 1		Cx 2 dx		2			2x						2		4							2	2			2		2
				2						1			2									2				2
										1
Следовательно:
3C	2 1 C 2
2
	0, x 1
		1 x 2
f(x)= 2x 2,		1 x 2

	0, x>2
Функция распределения равна:
		0, x 1
		x					x		2x
			2)dx					2				x	x			2	2x 1,							1 x 2
								2				x				2
F(x) f (x)dx (2x												1


		1, x>2
Математическое ожидание равно:

M(X) xf (x)dx

	2		2		2		x dx				1		x	3			1	x	2			2		8	2		1		1	5
	2		2		2						1			3			1		2			2		8			1		1	5
M(X) x 2(x 1)dx 2 x
	1		1								3						2				1			3			3		2	6
	1		1								3						2				1			3			3		2	6

Дисперсия равна:


D(X) x2 f (x)dx M 2 (X)

2					5		2	2						2			2				2
2							2	2													2
D(X) x		2	2(x 1)dx					2 x		3	x	2			x	4		x		3
D(X) x			2(x 1)dx					2 x			x		dx		x			x
1					6			1						4			3				1
1					6			1						4			3				1
8 16	1		2	17
3	2		3	6
Вероятность P(1 X 1.5)						равна:
P(1 X 1.5) F(1.5) F(1)								3	2					(1	2 1)				1
P(1 X 1.5) F(1.5) F(1)											3 1			(1	2 1)
								2											4
								2											4
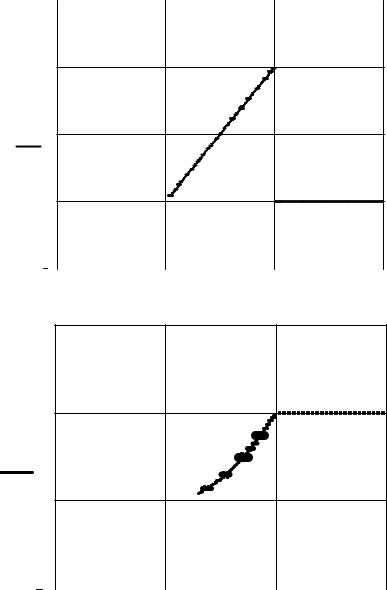
Графики	f(x) и F(x):
			3
			3

f(x) 1

1
1	0	1	2	3
			x

F(x)

1
1	0	1	2	3	8
			x		8
			x

Задача №9

По выборке одномерной случайной величины

построить график эмпирической функции распределения F* x ,

построить гистограмму относительных частот равноинтервальным способом,

вычислить точечные оценки математического ожидания и дисперсии,

вычислить интервальные оценки математического ожидания и дисперсии при доверительной вероятности 0,95,

выдвинуть гипотезу о законе распределения случайной величины и проверить ее при помощи критерия Пирсона при уровне значимости 0,05.

Одномерная выборка:

xi	19,80-19,85	19,85-19,90	19,90-19,95	19,95-20,00	20,00-20,05	20,05-20,10
ni	6	15	27	32	14	6

Решение

Согласно условию имеем:

n 100объем выборки;0.05 - шаг интервала.

Составим таблицу:

Интервал	xi	mi	mi/n	ximi	xi2mi
-∞;19.8	-∞	0	0	0	0
19.8;19.85	19.825	6	0.06	118.95	2358.184
19.85;19.9	19.875	15	0.15	298.125	5925.234
19.9;19.95	19.925	27	0.27	537.975	10719.152
19.95; 20	19.975	32	0.32	639.2	12768.02
20; 20.05	20.025	14	0.14	280.35	5614.009
20.05; 20.1	20.075	6	0.06	120.45	2418.034
20.1;∞	∞	0	0	0	0
∑		100	1	1995.05	39802.633

Эмпирическая функция распределения будет иметь вид:

		0	x 19.8
		0.06	19.8 x 19.85
			19.85 x 19.9
		0.21	19.85 x 19.9
F	*		19.9 x 19.95
F		(x) 0.48	19.9 x 19.95
		0.8	19.95 x 20
			20 x 20.05
		0.94	20 x 20.05
			x 20.05
		1	x 20.05

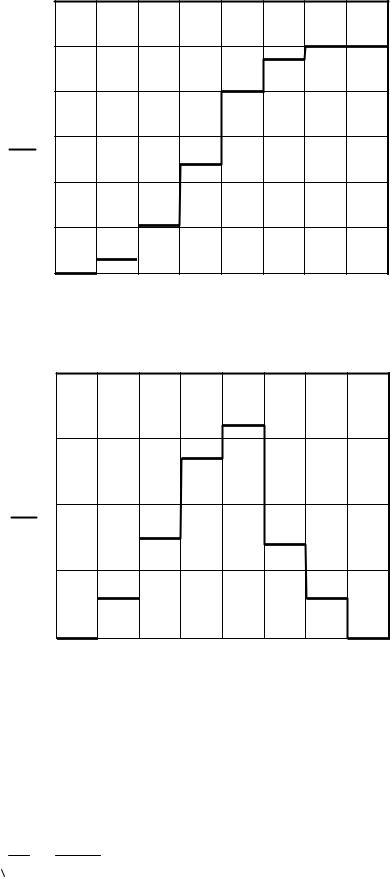
Строим график функции F*(x):

1.2

0.8

F(x) 0.6

0.4

0.2

19.75 19.8 19.85 19.9 19.95 20 20.05 20.1 20.15 x

Строим гистограмму относительных частот равноинтервальным способом:

0.4

0.3

f(x) 0.2

0.1

19.75 19.8 19.85 19.9 19.95 20 20.05 20.1 20.15 x

Вычислим точечные оценки:

	1	ximi			1	1995.05 19.951 - точечная оценка математического ожидания
x
	n			100
		1					n		1		100
			xi2mi							39802.633-		(19.95)2 0.0039-
D								x2
		n 1					n 1		100 1		100 1

точечная оценка дисперсия

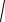D 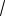0.0039 0.063среднее квадратическое отклонение

Вычислить интервальные оценки математического ожидания и дисперсии при доверительной вероятности 0,95.

Доверительный интервал для математического ожидания имеет вид:

I (mX ) x z n ;x z n ,

где z			- значение аргумента функции Лапласа, т.е Ф z		.
	argФ	2		2

Получаем

z0.95 argФ 0.295 1.96

Значит

I0.95 (mX ) 19.951 1.96 0.063;19.951 1.96 0.063 19.938;19.963100 100

Доверительный для дисперсии имеет вид:


					2				2					2
I	(D	X	)		2	z			2	2; 2 z				2			2
I	(D		)			z				2; 2 z							2
									n 1					n		1
Значит									n 1					n		1
Значит

							2				2				2			2		2		2
I0.95 (DX )				0.063				1.96					0.063			;0.063			1.96		0.063
I0.95 (DX )				0.063				1.96			100	1	0.063			;0.063			1.96	100 1	0.063
											100	1								100 1
0.0028;0.005

По форме гистограммы делаем предположение о нормальном законе распределения.

Проверим выдвинутую гипотезу при помощи критерия Пирсона при уровне значимости 0,05.

Составим таблицу для определения величины p2 :

				x			x				(m		np	)2
				x	i	x	x		x		(m		np	)2
m	x	x	i 1	F	i		F	i 1		p		i	i
i	i		i 1							i			npi
													npi
0	-∞	19.8			0		0.0081			0.0081		0.807
6	19.8	19.85		0.0081			0.0541			0.046		0.425
15	19.85	19.9		0.0541			0.2098			0.1557		0.021
27	19.9	19.95		0.2098			0.4968			0.287		0.101
32	19.95	20		0.4968			0.7856			0.2888		0.337
14	20	20.05		0.7856			0.9447			0.1591		0.229
6	20.05	20.1		0.9447			0.9916			0.0469		0.367
0	20.1	∞		0.9916				1		0.0084		0.843
∑										1			3

1 / 21 2 > Следующая >>>

Соседние файлы в предмете Теория вероятностей и математическая статистика

#
01.04.2014298.36 Кб148контрольная работа по ТВиМС.docx
#
01.04.2014203.38 Кб198контрольная работа,вариант20.docx
#
01.04.2014424.96 Кб145контрольная работа.doc
#
01.04.2014193.84 Кб389контрольная работа.docx
#
01.04.2014423.42 Кб348Контрольная работа№1 - Теория вероятностей и математическая статистика.doc
#
01.04.2014221.31 Кб317Кр по ТВиМС 4 вариант.pdf
#
01.04.20141.7 Mб117КР(1).doc
#
01.04.2014815.1 Кб166Кр.doc
#
01.04.2014519.17 Кб137Математическая статистика.doc
#
01.04.2014159.74 Кб142ответы ТР.doc
#
01.04.2014298.71 Кб133Пример контрольной работы.pdf