1. Лекции Термодинамика (УЭИ)
.pdf60
13.Что такое холодильный коэффициент и как он определяется?
14.Первый и второй интегралы Клаузиуса.
15.Каково изменение энтропии в замкнутой адиабатной системе, если в ней протекают обратимые и необратимые процессы?
16.Что такое эксергия? Основные формулы для расчета эксергии.
17.Можно ли считать эксергию параметром?
18.Эксергетический КПД.
Рекомендуемая литература:
Основная
10.Баскаков А. П., Берг Б.В., Витт О.К. и др. Теплотехника: учебник для вузов. 2-е изд., перераб. – М.: Энергоатомиздат, 1991. – Гл.3.
11.Нащокин В. В. Техническая термодинамика и теплопередача. – М.: Высшая школа, 1980. – §§ 8-1 - 8-14.
12.Техническая термодинамика: учебник для вузов/ В.А. Кириллин, В.В. Сычев, А.Е. Шейндлин. – 4-е изд., перераб. - М.: Энергоатомиздат, 1983. - Гл. 3, гл.9, п.
9.4.
Дополнительная
10.Сивухин Д.В. Общий курс физики. Т.2, Термодинамика и молекулярная физи-
ка. 2-е изд., испр. - М.: Наука, 1979. - Гл.3, §§27-30, 34-35, 37-38, 40-42.
11.Пригожин И., Кондепуди Д. Современная термодинамика. От тепловых двигателей до диссипативных структур: Пер. с англ. Ю. А. Данилова и В. В. Белого - М.:
Мир, 2002. – п.3.1 – 3.8.
12.Бродянский В.М., Фратшер В., Михалек К. Эксергетический метод и его приложения. Под ред. B.М. Бродянского. - М.: Энергоатомиздат, 1988. - 288 с.
13.Второе начало термодинамики / Под ред. и с предисл. А.К. Тимирязева. Сборник работ (С. Карно, Р. Клаузиус, В. Томсон-(Кельвин), Л. Больцман, М. Смолуховский). Изд. 2-е.- М.: Изд-во ЛКИ, 2007. - 312 с.
61
5 ТЕРМОДИНАМИЧЕСКИЕ ПРОЦЕССЫ ИДЕАЛЬНЫХ ГАЗОВ
5.1 Исследование термодинамических процессов
Основными термодинамическими процессами, весьма важными и в теоретическом и в прикладном отношениях, являются:
•изохорный, протекающий при постоянном объеме;
•изобарный, протекающий при постоянном давлении;
•изотермический, происходящий при постоянной температуре;
•адиабатный – процесс, при котором отсутствует теплообмен с окружающей средой;
•политропный – любой процесс, в котором теплоемкость постоянна
c = const.
Исследование процессов состоит в следующем:
а) выводится уравнение процесса, устанавливающее связь между начальными (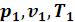
) и конечными параметрами идеального газа (
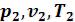) в данном процессе;
б) определяются изменения калорических параметров состояния системы в процессе (внутренней энергии u, энтальпии h, энтропии s);
изменение внутренней энергии
изменение энтальпии
изменение энтропии
62
При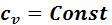 
и 
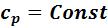для идеальных газов справедливы выражения (см. п.4.2):
в) вычисляются термодинамическая работа (расширения или сжатия)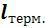 
и потенциальная (располагаемая) работа процесса 
.
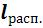г) определяется количество теплоты q, участвующей в процессе:
е) строится графическое изображение процесса в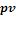 
- и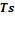 
- координатах.
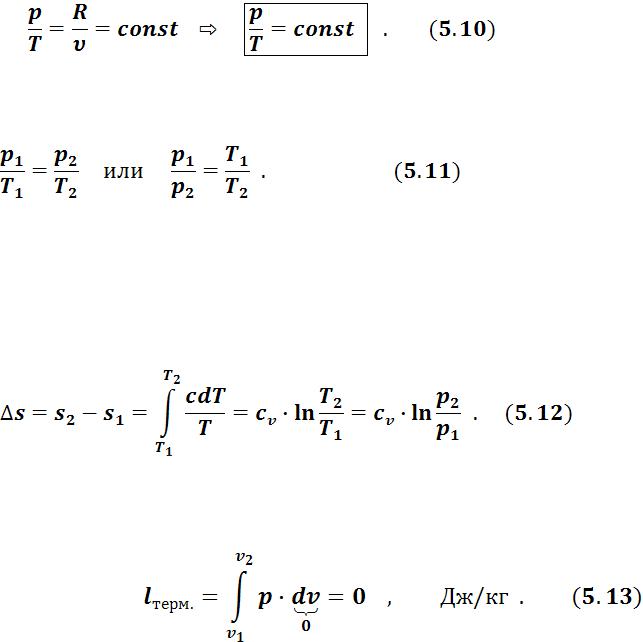
63
5.2Частные термодинамические процессы
5.2.1Изохорный процесс (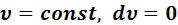 
)
а) Уравнение процесса
Из уравнения состояния идеального газа (2.13) получим:
Это и есть уравнение изохорного процесса (закон Шарля (п.2.1)). Он устанавливает следующую связь между начальными и конечными параметрами:
б) Изменения калорических параметров состояния:
изменение внутренней энергии определяется по общей формуле (5.1); изменение энтальпии определяется по общей формуле (5.2)
изменение энтропии определяется из формул (5.3) или (5.6) при
:
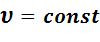в) Работа процесса:
•Термодинамическая работа в изохорном процессе по формуле (5.7) равна 0.
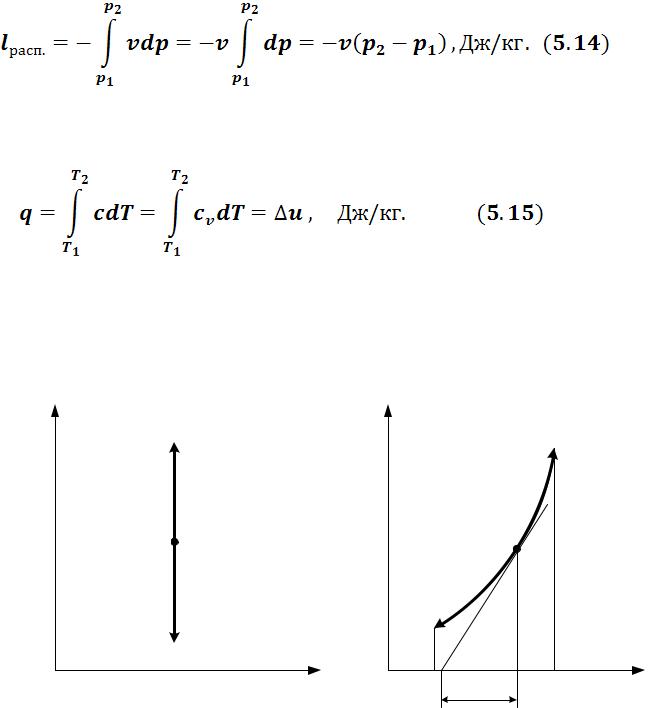
• Располагаемая (потенциальная) работа процесса из формулы (5.8).
64
г) Количество теплоты, подведенной (отведенной) в процессе из (5.9) при
:
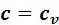В изохорном процессе вся подводимая теплота идет на увеличение внутренней энергии.
е) Графическое изображение процесса в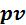 
– и 
- координатах.
Изображение изохорного процесса представлено на рисунке 5.1.
P |
|
T |
|
2 |
2 |
|
|
|
|
lрасп < 0 |
|
lрасп > 0
1 |
|
1 |
|
|
|
|
2' |
> 0 |
|
q |
|
|
|
|
2' |
q < 0 |
|
|
|
|
v |
c |
s |
|
v |
|
Рисунок 5.1 – Изохорный процесс
•
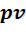- диаграмма. Поскольку 
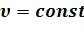на 
- диаграмме изохорный процесс изображается вертикалью. Термодинамическая работа (площадь проекции под линией процесса на ось V ) равна 0.
Располагаемая работа в процессе 1-2 (dp> 0) отрицательна. В процессе 1-2’ давление уменьшается (dp< 0) и располагаемая работа положительна.
65
•Tsдиаграмма. Согласно уравнению (5.12)изохора в Ts - координатах имеет логарифмический характер с выпуклостью к оси s. Тангенс угла наклона касательной равен:
Сувеличением температуры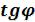 
возрастает. А подкасательная в любой точке изохоры численно равна истинной изохорной теплоемкости
.
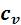Теплота, подведенная в процессе, изображается на Ts - диаграмме площадью под линией процесса. Процесс 1–2, связанный с увеличением энтропии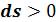 
, сопровождается подводом теплоты 
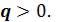Процесс 1– 2’, связанный с уменьшением энтропии 
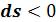, сопровождается отводом теплоты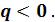 
5.2.2Изобарный процесс ( 
)
а) Уравнение процесса
Из уравнения состояния идеального газа (2.13) получим:
Это - закон Гей–Люссака (п.2.1), устанавливающий следующую связь между начальными и конечными параметрами:
б) Изменения калорических параметров состояния:
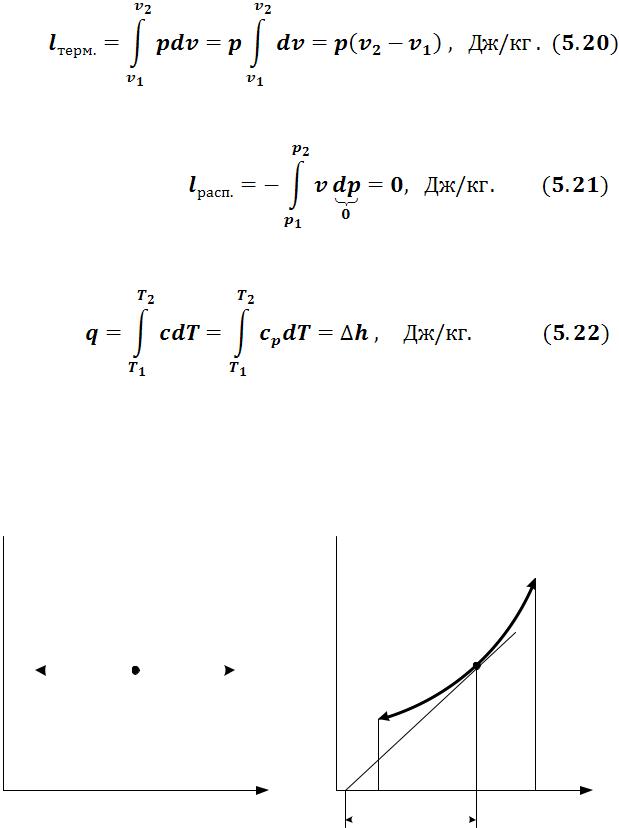
Изменение внутренней энергии определяется по общей формуле (5.1); Изменение энтальпии определяется по общей формуле (5.2) Изменение энтропии определяется из формул (5.3), (5.6) при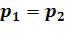 
:
66
в) Работа процесса:
•Термодинамическая работа в изобарном процессе при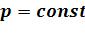 
:
•Располагаемая (потенциальная) работа в изобарном процессе равна 0:
г) Количество теплоты, подведенной (отведенной) в процессе при c = cp:
В изобарном процессе вся подводимая теплота идет на увеличение энтальпии.
е) Графическое изображение процесса в 
– и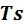 
- координатах.
Изображение изобарного процесса представлено на рисунке 5.2.
P 
T 
2
2' |
1 |
2 |
|
1 |
||
|
|
|
||||
|
|
|
|
2' |
|
|
|
|
|
|
|
|
|
|
lтерм < 0 |
lтерм > 0 |
|
|
|
|
|
|
|
|
q < 0 |
|
q > 0 |
|
|
|
v |
cp |
|
s |
|
|
|
|
|
|
|
Рисунок 5.2 – Изобарный процесс
67
•
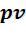- диаграмма. Термодинамическая работа изображается площадью под линией процесса при проецировании на ось V. Работа расширения (процесс 1–2) считается положительной. Работа, затраченная на сжатие (процесс 1–2’) – отрицательной.
Располагаемая работа в изобарном процессе равна 0.
•Tsдиаграмма. Согласно уравнению (5.19) изохора в Ts - координатах имеет логарифмический характер с выпуклостью к оси s. Тангенс угла наклона касательной равен:
Сувеличением температуры 
возрастает. А подкасательная в любой точке изохоры численно равна истинной изохорной теплоемкости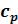 
.
Теплота, подведенная в процессе, изображается на Ts - диаграмме площадью под линией процесса. Процесс 1–2, связанный с увеличением энтропии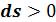 
, сопровождается подводом теплоты 
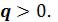Процесс 1–2’, связанный с уменьшением энтропии 
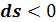, сопровождается отводом теплоты
5.2.3 Изотермический процесс (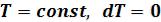 
)
а) Уравнение процесса
Из уравнения состояния идеального газа (2.13) получаем:
Это - закон Бойля–Мариотта, (п.2.1), устанавливающий следующую связь между начальными и конечными параметрами:
68
б) Изменения калорических параметров состояния:
изменение внутренней энергии
изменение энтальпии
В изотермическом процессе внутренняя энергия и энтальпия идеального газа не изменяются.
изменение энтропии определяется из формул (5.4, 5.5) при T1 = T2
в) Работа процесса:
• Термодинамическая работа при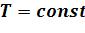 
:
• Располагаемая (потенциальная) работа.
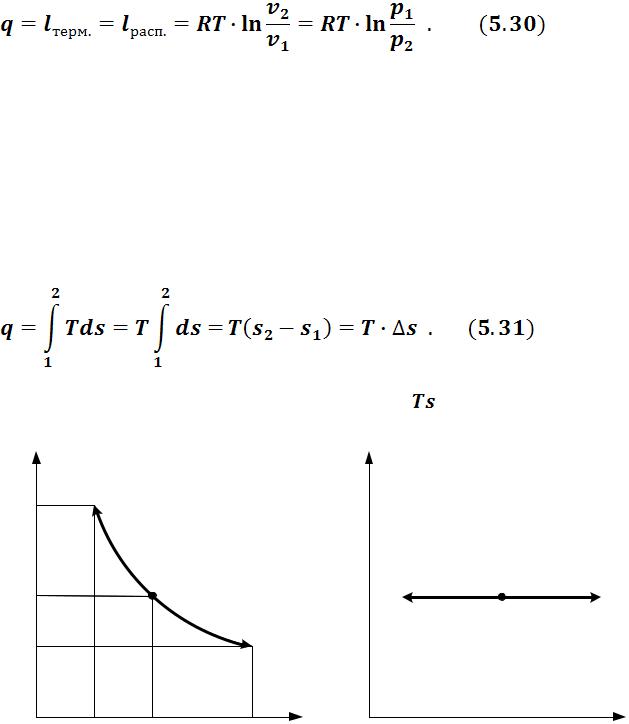
Учитывая, что u = 0 и h = 0, из I-го закона термодинамики (3.24, 3.26) получим
69
В изотермическом процессе количество теплоты, термодинамическая и располагаемая работы равны между собой.
г) Количество теплоты, подведенной (отведенной) в процессе.
Согласно выражению (5.30) в изотермическом процессе вся подводимая теплота расходуется на совершение работы, т.е. количество теплоты можно определить по уравнению (5.30). С другой стороны количество теплоты, участвующей в изотермическом процессе, можно рассчитать из определения энтропии (4.18):
е) Графическое изображение процесса в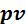 
- и
Изотермический процесс показан на рисунке 5.3.
P |
T |
|
2' |
lрасп < 0 |
|
|
1 |
2' |
|
lрасп > 0 |
2 |
|
< 0 |
||
|
||
lтерм |
lтерм > 0 |
|
|
||
|
v |
- координатах.
1 |
2 |
q < 0 |
q > 0 |
s
Рисунок 5.3 – Изотермический процесс
•
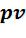- диаграмма. Согласно уравнению (5.24) изотерма является равнобо-
кой гиперболой с асимптотами, совпадающими с осями координат. В
процессе расширения 1-2 (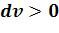
; 
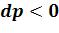) и термодинамическая и рас-
полагаемая работы положительны. В процессе сжатия 1-2’ (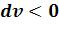
;
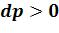) обе работы отрицательны.