31. Арифметические действия над действительными числами.

При сложении действительных чисел с одинаковыми знаками нужно сложить их модули и перед суммой поставить их общий знак. Например, (+3)+(+8)=+11; (-4)+(-9)=-13. При сложении двух действительных чисел с разными знаками модуль суммы равен разности модулей слагаемых. Знак суммы есть знак слагаемого, где модуль больше. Например, (+3)+(-9)=-6; (+11)+(-7)=+4. Вычитание действительных чисел можно заменить сложением: a- b = а + (-b), то есть, чтобы вычесть из числа а число b, достаточно к уменьшаемому прибавить число, противоположное вычитаемому. Например: (+3)-(-8)=(+3)+(+8)=11; (+4)-(+9)=(+4)+(-9)=-5. При умножении (делении) двух действительных чисел нужно умножить (разделить) их модули. Перед результатом нужно поставить знак по правилу знаков из таблицы знаков. Таблица знаков:

при умножении	при делении
(+)*(+)=(+)	(+):(+)=(+)
(-)*(-)=(+)	(-):(-)=(+)
(+)*(-)=(-)	(+):(-)=(-)
(-)*(+)=(-)	(-):(+)=(-)

Свойства операции умножения действительных чисел: 1.Коммутативный закон сложения: для любой пары чисел а и б: а*б=б*а. 2. Ассоциативный закон умножения: для любой тройки чисел а, б и с: (а*б)*с=а*(б*с).

33. Правило округления чисел и арифметические действия с приближёнными числами.

Числа округляют, когда полная точность не нужна или невозможна. Натуральные числа округляют до десятков, сотен, тысяч и т.д.

Правила:

1) если первая отброшенная цифра меньше 5, то остав­шиеся десятичные знаки сохраняют без изменения;

2) если первая отброшенная цифра больше 5, то к пос­ледней оставшейся цифре прибавляют единицу;

Пример: Число 25,863 округлённо записывается как – 25,9. В данном случае цифра 8 будет усилена до 9, так как первая отсекаемая цифра 6, больше чем 5.

3) В случае если первая из отсекаемых цифр меньше чем 5, то усиления не производится.

Пример: Число 46,48 округлённо записывается как – 46. Число 46 наиболее близко к округляемому числу, чем 47.

4) если первая из отброшенных цифр равна 5 и все от­брошенные цифры являются нулями, то последняя остав­шаяся цифра оставляется неизменной, если она четная, если не четная то усиливается на единицу.

Пример: Число 0,0465 округлённо записывается как – 0,046. В данном случае усиления не делается, так как последняя оставляемая цифра 6 является чётной.

Число 0,935 округлённо записывается как – 0,94. Последняя оставляемая цифра 3 усиливается, так как она является нечётной.

Арифметические действия с приближёнными числами.

При сложении и вычитании приближенных чисел. В окончательном результате следует сохранять столько десятичных знаков, сколько их имеется в слагаемом (или вычитаемом), содержащем наименьшее количество десятичных знаков.

Поэтому перед сложением (вычитанием) приближенные числа необходимо округлить, оставив в них на один десятичный знак больше, чем в слагаемом (вычитаемом), имеющем наименьшее количество десятичных знаков. После сложения (вычитания) чисел окончательный результат округляют согласно вышеуказанному правилу.

Пример. Сложить приближенные числа 215,635+1,2+26,18+24,997. Наименьшее количество десятичных знаков имеет число 1,2. Поэтому, согласно правилам, следует складывать числа: 215,64+1,2+26,18+25,00=268,02 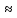268,0.

Умножение, деление, возведение в степень

Точность окончательного результата умножения, деления и возведения в степень приближенных чисел зависит от количества значащих цифр в исходных данных, в связи с чем необходимо соблюдать следующие правила.

1. При умножении и делении приближенных чисел в окончательном результате следует сохранять столько значащих цифр, сколько их имеется в числе (в сомножителе, делимом, делителе) с наименьшим количеством значащих цифр.

Поэтому при умножении или делении чисел с разным количеством значащих цифр их округляют, оставляя на одну значащую цифру больше, чем в числе с наименьшим количеством значащих цифр. После выполнения арифметических действий окончательный результат округляют согласно правилу. Пример. Вычислить произведение приближенных чисел 106,504Х1,ЗХ0,3085. Округлив сомножители, получим: 107Х 1,3X0,308=42,8428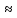43.

2. При возведении приближенного числа в степень в окончательном результате следует сохранять столько значащих цифр, сколько их содержится в основании данного числа. Примеры:;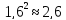

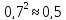
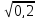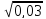3. При извлечении корня в окончательном результате следует сохранять столько значащих цифр, сколько их имеется в подкоренном числе. Примеры: =0,4; =0,2