
- •3. Определение «умножения» с точки зрения различных подходов к построению множества целых неотрицательных чисел(). С примерами.
- •5. Определение вычитания с позиций различных подходов к построению множества целых неотрицательных чисел.
- •7. Доказательство теоремы невозможности деления на «0».
- •11. Понятие натурального числа и нуля с точки зрения теоретико-множественного подхода. Примеры.
- •13. Отношение «равно», «меньше», «больше» на множестве целых неотрицательных чисел ().
- •15. Определение произведения с теоретико-множественных позиций, связанного с понятием Декартового произведения множеств.
- •17. Определение частного целого неотрицательного числа на натуральное.
- •19. Натуральное число, как мера отрезка.
- •21. Задача расширения понятия числа.
- •23. Множество целых чисел. Свойства множества целых чисел и их геометрическую интерпретацию.
- •25. Арифметические действия над рациональными числами.
- •27. Десятичные дроби. Алгоритмы арифметических действий над ними.
- •29. Действительные числа. Понятие иррациональных чисел.
- •31. Арифметические действия над действительными числами.
- •33. Правило округления чисел и арифметические действия с приближёнными числами.
27. Десятичные дроби. Алгоритмы арифметических действий над ними.
1. Принцип поместного
значения цифр применяется при записи
дробей: переход в значении числа на одно
место влево увеличивает значение цифр
в q
раз. Переход на одно место вправо
уменьшает ее значение во столько же
раз; Поставив справа от цифр единиц
знак «дробности» (запятую) понимают
цифру, написанную на 1ом месте справа
от запятой, как обозначение числителя
дроби со знаменателем
 ,
на 3-ем
,
на 3-ем
 .
Тогда выражение,
.
Тогда выражение,
 ,
,
 ,….,
,….,

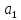 ,
,
 ,
, ,….,
,…., – это запись суммы
– это запись суммы
 +
+ +
+ +
+ +
+ +…..+
+…..+
Пример: при q=
3 запись 201,12202 означает число:
2* +0*3+1+
+0*3+1+ +
+ +
+ +
+ +
+
Определение: десятичной дробью называется любая дробь со знаменателем, представляющим собой степень 10 при условии, что эта дробь записана по принципу поместного значения цифр без знаменателя.
По определению:
 -
обыкновенная дробь; 0,173- десятичная
дробь.
-
обыкновенная дробь; 0,173- десятичная
дробь.
Ценная часть десятичной дроби называется характеристикой, дробная часть – мантиссой.
2. Сложение и вычитание десятичных дробей. Эти операции выполняются так же, как и сложение, и вычитание целых чисел. Необходимо только записать соответствующие десятичные знаки один под другим.
Умножение десятичных дробей. На первом этапе перемножаем десятичные дроби как целые числа, не принимая во внимание десятичную точку. Затем применяется следующее правило: количество десятичных знаков в произведении равно сумме десятичных знаков во всех сомножителях. Замечание: до простановки десятичной точки в произведении нельзя отбрасывать нули в конце!
Деление десятичной дроби на целое число. Если делимое меньше делителя, записываем ноль в целой части частного и ставим после него десятичную точку. Затем, не принимая во внимание десятичную точку делимого, присоединяем к его целой части следующую цифру дробной части и опять сравниваем полученную целую часть делимого с делителем. Если новое число опять меньше делителя, ставим ещё один ноль после десятичной точки в частном и присоединяем к целой части делимого следующую цифру его дробной части. Этот процесс повторяем до тех пор, пока полученное делимое не станет больше делителя. После этого деление выполняется, как для целых чисел. Если делимое больше делителя или равно ему, сначала делим его целую часть, записываем результат деления в частном и ставим десятичную точку. После этого деление продолжается, как в случае целых чисел.
Деление одной десятичной дроби на другую. Сначала переносим десятичные точки в делимом и делителе на число десятичных знаков в делителе, то есть делаем делитель целым числом. Теперь выполняем деление, как в предыдущем случае.
29. Действительные числа. Понятие иррациональных чисел.
Множество действительных чисел - это вместе взятые множества рациональных и иррациональных чисел.
Действительное число или как его еще называют вещественное число - это любое положительное число, отрицательное число или нуль.
Действительные числа разделяются на рациональные и иррациональные.
Вещественные (действительные) числа - это своего рода математическая абстракция, служащая для представления физических величин. Такие числа могут быть интуитивно представлены как отношение двух величин одной размерности, или описывающие положение точек на прямой. Множество вещественных чисел обозначается и часто называется вещественной или числовой прямой. Формально вещественные числа состоят из более простых объектов таких, как целые и рациональные числа. Множество действительных чисел обозначается - R
Иррациональные числа – это действительные числа, не являющиеся рациональными и так же - это числа, которые в десятичной записи представляют собой бесконечные непериодические десятичные дроби.
Например, бесконечная непериодическая десятичная дробь 4,10110011100011110000… (количество единиц и нулей каждый раз увеличивается на одну) является иррациональным числом. Приведем еще пример иррационального числа: −22,353335333335… (число троек, разделяющих восьмерки, каждый раз увеличивается на две).
Иррациональные числа достаточно редко встречаются именно в виде бесконечных непериодических десятичных дробей. Обычно они встречаются в виде корней, степеней, логарифмов и т.п., а также в виде специально введенных букв. Самыми известными примерами иррациональных чисел в такой записи являются арифметический квадратный корень из двух , число «пи» π=3,141592…, число e=2,718281.
