
Математика УНК 1 курс экз / Математика готовые шпоры
.docx|
1. Понятие об аксиоматическом методе построении теории. Аксиомы Пеано При аксиоматическом построении теории выбирают не определенные понятия, принимая их за исходные, а так же отношения между ними и называют их основными понятиями. Все остальные понятия должны быть строго определены, затем формулируется высказывание выражающие свойства этих понятий и отношений. Эти высказывания (предложения) называются аксиомами данной теории. Аксиомы принимаются без доказательства, но на их основе доказываются другие предложения данной теории, которые называются теоремами. В аксиоматической теории аксиомы не доказываются, однако, аксиомы являются отражением деятельности людей, что обуславливает их справедливость. Система аксиом должна удовлетворять следующим требованием: А) Непротиворечивой т.е делая выводы из данной системы аксиом никогда не придёт к противоречию Пример: 1)Для
любого а
существует элементы б
такой, что а 2)Не
для одного а
не выполняется, что а 3)Если
а 4)Если
а Возьмем
(эквивалент) а
ему найдется б
(1 аксиома) по аксиоме (3) а По
аксиоме (4) а Никакая аксиома не должна быть следствием остальных аксиом этой системы т.е она должна быть независимой. При построении теорем можно использовать различные системы аксиом но они должны быть равносильными. Аксиомы Пеано. За основным отношением было взято непосредственно следовать за. Аксиома 1. В множестве N существует элемент, непосредственно не следующий ни за каким элементом этого множества. Будем называть его единицей и обозначать символом 1. Аксиома 2. Для каждого элемента а из N существует единственный элемент а, непосредственно следующий за а. Аксиома 3. Для каждого элемента а из N существует не более одного элемента, за которым непосредственно следует а. Аксиома 4.Всякое подмножество М множества N совпадает с N, если обладает свойствами: 1) 1 содержится в М; 2) из того, что а содержится в М, следует, что и а' содержится в М.
|
2.
Определение «сложение» с точки зрения
различных подходов к построению целых
неотрицательных чисел ( По
аксиоматической теории определение
сложение
N
чисел
вводим, опираясь на основные понятия
теории, кроме того используется понятие
«алгебраическая операция». Основное
понятие
– если к любому N
числу а
прибавить
1, то получим а’,
непосредственно следующей за а.
Разберем, как прибавляется к а
в Итак,
получается следующее определение:
сложением N
чисел называется алгебраическая
операция, определенная на мн N
чисел и обладающая свойствами: 1.( Если
брать теоретико-множественный подход,
то сложение – это операция «объединение»
множеств A
|
3.
Определение «умножения» с точки зрения
различных подходов к построению
множества целых неотрицательных
чисел( По правилам построения аксиоматической теории определить умножение N чисел можно, используя отношение «непосредственно следовать за» и понятия. Основное
понятие: Если для любого N
числа
умножить
на 1, то получится а,
т.е.
имеет место равенство, а
1 = а.
Теперь разберем, как умножить а и б,
где б Пример: Если известно, что 7 5 = 35, то для нахождения произведения 7 6 достаточно к 35 прибавить 7, так как 7 6 = 7(5 + 1) = 7 5 + 7. Т.е нужно знать а и числа за которыми следует б+1 т.е а(б+1)= а*б+а= а*б= a*б+а Определение. Умножением N чисел называется алгебраическая операция, определенная на множестве N чисел обладающая свойствами: 1) ( а N) а 1 а. 2) ( а, b N) а b' = а b+а. Число а b называется произведением чисел а и b, а сами числа а и b- множителями. Определение.
Умножение
Особенностью данного определения, так же как и определения сложения натуральных чисел, является то, что заранее неизвестно, существует ли алгебраическая операция, обладающая указанными свойствами, а если существует, то единственная ли она, поэтому существует теорема. Теорема 1 сложение(умножение) N чисел существует и оно единственно.
|
4.
Таблицы сложения и умножения в
аксиоматическом построении мн.
Используя
определение сложения (сложением
N
чисел называется алгебраическая
операция, определенная на мн N
чисел и обладающая свойствами: 1.( а) 1+1=1’(условие №1из определения сложения). Обозначим 1’ символом «2» => 1+1=1’=2. Аналогично 2+1=2’=3 и т.д. б)1+2=1+1’=(1+1)’=2’=3 (условие №2 в определении сложения) 2+2=2+1’=(2+1)’=3’=4 (по условию 2 из определения сложения). Аналогично 2+3=2+2’=(2+2)’=4’=5. Используя определения умножения ( Умножением N чисел называется алгебраическая операция, определенная на множестве N чисел обладающая свойствами: 1) ( а N) а 1 а. 2) ( а, b N) а b' = а b+а.), теорему 1(сложение (умножение) N чисел существует и оно единственно) и таблицу сложения, составим таблицу умножения N чисел: а) 1*1=1, 2*1=2, 3*1=3 и т.д. – условие №1 в определении умножения б)1*2=2=1*1’=1*1+1=2 (условие №2 в определении умножения при переходе 1*1’=1*1; 1*1+1=1+1 - результат, полученный на этапе а); 1+1 = 2 на основании таблиц сложения. Аналогично 1*3=1*2’=1*2+1=2+1=3 и т.д. в) 2*2=2*1’=2*1+2=2+2=4 и т.д.
|
5. Определение вычитания с позиций различных подходов к построению множества целых неотрицательных чисел. По аксиоматической теории N чисел вычитание определяется, как операция обратная сложению. Определение. Вычитанием N чисел а и б называется операция, удовлетворяющая условию: а-б=с тогда и только тогда, когда б+с=а. Число а-б называется разностью чисел а и б, число а- уменьшаемым, а число б-вычитаемым. Для
Для
|
6.
Определение деления мн
По аксиоматической теории N чисел деление определяется как операция, обратная умножению. Определение – частным N чисел а и b называется N число с=a:b, удовлетворяющее условию, что b*c=a. Действие называется делением, число а – делимым, b-делителем. Правило деления разности на число. Для того чтобы разделить разность на число, достаточно разделить это число на уменьшаемое и вычитаемое и из первого частного вычесть второе. Пусть числа а и b делятся на число с, то и их сумма а – b делится на с, т.е. (а – b):с =а : с – b : с. Правило деления числа на произведение. Для того чтобы разделить число на произведение, достаточно это число разделить на один множитель, а затем полученное частное разделить на другой множитель. Пусть натуральное число а делится на натуральные числа b и с, то а : (b*с) = (a : b) : c = (a : c) : b. Правило деления произведения на число. 1.Если натуральное число а делится на натуральное число с, то для любого натурального числа b произведение а*b делится на с. При этом частное, получаемое при делении произведения а*b на число с, равно произведению частного, получаемого при делении на с, и числа b : (а*b) : с = (а : с)*b. |
7. Доказательство теоремы невозможности деления на «0». Доказательство. Пусть даны целое неотрицательное число а и b = 0. Рассмотрим случай, когда а 0, Предположим, что частное такого числа и нуля существует. Тогда, по определению деления, найдется такое целое неотрицательное число c, что а – с =0, откуда а = 0. Пришли к противоречию с условием, значит, частное чисел а 0 и b = 0 не существует. Пусть теперь а = 0. Предположим опять, что частное а = 0 и b = 0 существуют, и тогда найдется такое целое неотрицательное число с, что выполняется равенство 0 = с0, истинное при любых значениях с. Таким образом, частным чисел а = 0 и b= 0 может быть любое целое неотрицательное число, т.е. результат деления определяется не единственным образом. Поэтому деление нуля на нуль также невозможно.
|
8. Определение деления с остатком Определение
– пусть a
и
b
– N
числа. Неполным частным q
с остатком r
при делении a
на
b
называются такие
Теорема:
|
9.
Свойства
множества целых неотрицательных чисел
Множества N чисел обладает свойствами: 1. оно бесконечно 2. Упорядочено при помощи отношений «меньше» 3. Дискретное 4. в нем есть наименьшее число единица. Свойства множеств N чисел: 1.
для всех N
чисел 1/ед является наименьшим числом
т.к а`=а+1=1+а а<а' и 1<а' 2. свойства дискретности множества N чисел(а и а+1 – называются соседними) т.е не для одного N числа а нет такого N числа n, что n стоит между a<n<a+1 3.
упорядоченное множество т.к для любых
2х Nчисел
а и б имеет место одной из следующих
соотношений: либо а= Определение. Число а меньше числа б(а<б) тогда и только тогда, когда существует такое N число C что, а+с=б. Если а<б, то говорят б>а, а пишут б>а. Для того чтобы множество считалось упорядоченным нужно чтобы отношения меньше было транзитивным и антисимметричным |
10. Метод математической индукции Данный
метод основан на аксиоме Пеано №4
(пусть мн M
есть подмножество множества N,
и известно, что: а) единица содержится
в M,
б) из того, что a
содержится в M
=> что и а’
содержится в М, тогда мн М совпадает
с множеством N).
Теорема: если утверждение А(n)
с N
переменной n
истинно для n=1 Доказательство.
Обозначим через М множество
тех и только тех натуральных чисел,
для которых утверждение А(n) истинно.
Тогда из условия теоремы имеем: 1) 1 |
|
11. Понятие натурального числа и нуля с точки зрения теоретико-множественного подхода. Примеры. Хотя количественные числа являются, как бы вторичными по отношению к порядковому числу тем не менее исторически оно появилось ранее. Если множествами А и B соответствует одно и тоже число A то это означает, что они взаимно однозначно отображаются друг на друга и на один и тот же отрезок N ряда. Определение. 2 множества взаимно однозначно отображающиеся друг друга называются равномощными или множества A и B содержит поровну элементов т.к конечных множеств распадается на классы равномощных множеств. Пример: в один из классов поедет множество сторон треугольника, его вершины, букв в слове дым; В другом множестве сторон четырехугольника его вершин, множества может стола и др. Общее у всех множеств одного класса 1) Это число элементов так N число «три» 2) Общее свойство класса множества равномощных множеству сторон треугольника Теоретико-множественное
истолкование числа «ноль» заключается
в том, что оно ставится в соответствии
пустому множеству( Класс равномощных конечных множеств задается отрезком N ряда чисел. Пример:
класс конечных множеств содержащих
множество вершин квадрата задается
отрезками N
ряда
В
начальной школе изучение математики
начинается с усвоения отрезка N
ряда
|
12. Порядковые и количественные N числа, примеры. Одно
и тоже мн А не может быть взаимно-однозначно
отображено на 2 различных отрезках N
ряда чисел. Т.е. каждому конечному мн
А может быть поставлено в соответствии
такое число А, что мн А взаимно-однозначно
отображается на отрезок N
ряда
|
13.
Отношение «равно», «меньше», «больше»
на множестве целых неотрицательных
чисел ( Отношение равенства целых неотрицательных чисел обладает следующими свойствами: 1. Рефлексивность.Любое целое неотрицательное число равно самому себе, т.е. а = а. 2. Симметричность.Если число а равно числу в, то и число в равно числу а, т.е. если а = в, то в = а. 3. Транзитивность.Два числа, равные третьему, равны между собой, т.е. если а = в и в = с, то а = с. Доказательство.Каждое из этих свойств вытекает непосредственно из одноименного свойства отношения равномощности множеств и определения равенства натуральных чисел. Следствие.Отношение равенства целых неотрицательных чисел является отношением эквивалентности. Из
определения отношения «меньше»
в аксиоматической теории(число а
меньше числа б, если существует такое
N
число с, что а+с=б), в силу транзитивного
закона имеем, что а<б то из того что
х Определение.
(теоретико-множественная трактовка)
а<б в том и только в том случае когда
отрезок
Пример: Справедливость
4<8 вытекает из того что отрезок N
ряда
Свойства отношения «меньше» для N чисел имеют такую трактовку теоретико-множественном подходе: 1.
Транзитивность А 2.
Антисимметричность если A 3.
Справедливость утверждающего, что
0<а для любого а "отношение больше трактуется, так же как и меньше(Если множество А равномощно собственному подмножеству множества В и n{А} = а, n(В) = в, говорят, что число а меньше числа в, и пишут а < в. В этой же ситуации говорят, что в больше а, и пишут в > а.)" |
14. Теоретико-множественный смысл разности. В
аксиоматическом подходе вычитание
записывается так: а-b=c
( |
15. Определение произведения с теоретико-множественных позиций, связанного с понятием Декартового произведения множеств. Теорема:
пусть А и B
конечные множества, тогда их Декартово
произведение также является конечным
множеством, причем выполняется
равенство: n(A С
теоретико-множественной точки зрения
а*б
Пример: Сколько пуговиц нужно пришить на 3 таких пальто. 3множества-каждое пальто: n( n(
|
16. Определение произведения, в основе которого лежит понятие суммы нескольких слагаемых. Теорема:
Если число b>1,
то произведение чисел a
и
b
равно сумме b
слагаемых, каждое из которых равно a.
a*1=1,
a*0=0.
Определение
умножения:
если a
и b
-
|
17. Определение частного целого неотрицательного числа на натуральное. Определение.
Частным целого неотрицательного числа
а и натурального числа b называется
такое целое неотрицательное число с
= а:b, произведение которого и числа b
равно а.
Можно показать и наличие
обратной связи, т. е. что из второго
определения частного вытекает
первое:
а:b = с |
18. Теоретико-множественный смысл правил деления суммы и произведения на число. Используя теоретико-множественный подход к действиям над целыми неотрицательными числами, можно дать теоретико-множественное истолкование правила деления суммы на число: если частные а:с и b:с существуют, то (а +b):с = а:с + b:с. Пусть а =n(А) и b =n(В), причем А В =. Если множества А и В можно разбить на равночисленные подмножества, состоящие из с элементов каждое, то и объединение этих множеств допускает такое же разбиение. Если при этом множество А состоит из а:с подмножеств, а множество В – из b:с подмножеств, то А В состоит из а:с + b:с подмножеств. Это и значит, что(а + b ):с =а:с + b:с. Аналогично проводятся рассуждения и в случае, когда с рассматривается как число равночисленных подмножеств в разбиении множеств А и В.
|
19. Натуральное число, как мера отрезка. Выясняя смысл натурального числа как меры величины, все рассуждения будем вести на примере одной величины - длины отрезка. Уточним сначала понятие «отрезок состоит из отрезков». Определение.
Считают, что отрезок х состоит из
отрезков
В
этом же случае говорят, что отрезок х
разбит на отрезки
Пусть задан отрезок х, его длину обозначим X. Выберем из множества отрезков некоторый отрезок е, назовем его единичным отрезком, а длину обозначим буквой Е. Определение. Если отрезок х состоит из а отрезков, каждый из которых равен единичному отрезку е, то число а называют численным значением длины X данного отрезка при единице длины Е. Пишут:
X = а*Е или а =
Например,
отрезок х состоит из 6 отрезков, равных
отрезку е. Если длину единичного
отрезка обозначить буквой Е, а длину
отрезка х- буквой Х, то можно написать,
что Х = 6Е или 6 =
Из данного определения получаем, что что натуральное число как результат измерения длины отрезка (или как мера длины отрезка) показывает, из скольких единичных отрезков состоит отрезок, длина которого измеряется. При выбранной единице длины Е это число единственное. В связи с таким подходом к натуральному числу сделаем два замечания: 1. При переходе к другой единице длины численное значение длины заданного отрезка изменяется, хотя сам отрезок остается неизменным. Так, если в качестве единицы длины выбрать длину отрезка е₁, (рис. 120), то мера длины отрезка х будет равна числу 3. Записать это можно так: X = 3 ∙ Е ₁ или mE (X) = 3. 2. Если отрезок х состоит из а отрезков, равных е, а отрезок у - из b отрезков, равных е, то а = b тогда и только тогда, когда отрезки х и у равны. Аналогично можно истолковать смысл натурального числа и в связи с измерением других величин. Так, в записи 3 см2 число 3 означает, что фигура F состоит из трех единичных квадратов с площадью, равной квадратному сантиметру. |
20. Определение арифметических действий над числами, рассматриваемых как мерами отрезков. Если
отрезок а
составлен из отрезков в
и с
и мера отрезков в при единичном отрезке
е=1
meb
=p,
mec
=q, то mea
= p+q=meb
+ mec.
Доказательство: meb
=p => b=pe, mec=q
=> c=qe, тогда отрезок а
разбит на p+q отрезков, каждый из которых
= е, т.е. a=(p+q)e => mea
= p+q. Вывод: сумма 2 натур-ых чисел p и q
= мере отрезка
а,
который состоит из отрезков b
и c,
меры кот-ых при одной и той же единице
длины = p и q соответственно. Если мера
отрезка а
при единице длины e=p, a me1e
= q => me1a
= pq. Доказательство: mea=p
=> a=pe, me1=q
=> e=q |

 б
б а
а б
б б
б а
а
 б
и б
б
и б с
с
 (то)
а
(то)
а с
с б
б б
б а
а б
и б
б
и б а
а
 а
а а
(противоречие с аксиомой 2)
а
(противоречие с аксиомой 2)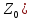 (с примерами).
(с примерами).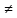 1:
к
3 прибавим 4 = 7. Чтобы найти к 3+5 достаточно
к 7 прибавить 1, т.е. взять число,
непосредственно следующее за 7 (т.к. в
сумме 3+5, 5 – это второе слагаемое,
непосредственно следующее за первым
слагаемым 4). Общий вид: а+(b+1)=(a+b)+1,
a+b’=(a+b)’.
1:
к
3 прибавим 4 = 7. Чтобы найти к 3+5 достаточно
к 7 прибавить 1, т.е. взять число,
непосредственно следующее за 7 (т.к. в
сумме 3+5, 5 – это второе слагаемое,
непосредственно следующее за первым
слагаемым 4). Общий вид: а+(b+1)=(a+b)+1,
a+b’=(a+b)’.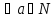 )
a+1=a’
; 2.(
)
a+1=a’
; 2.(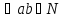 )
a+b’=(a+b)’.
Число a+b
называется суммой чисел a
и b,
а сами эти числа называются слагаемыми.
Определение:
сложение
)
a+b’=(a+b)’.
Число a+b
называется суммой чисел a
и b,
а сами эти числа называются слагаемыми.
Определение:
сложение
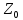 определяется так же, как и для N,
причём считается, что для .(
определяется так же, как и для N,
причём считается, что для .(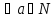 )
0+а=а+0=а.
)
0+а=а+0=а.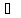 B.
B.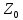 ).
С примерами.
).
С примерами.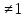
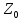 определяется так же, как и для N
чисел причем считают, что (
определяется так же, как и для N
чисел причем считают, что (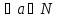 )
0*a=a*0=0.
)
0*a=a*0=0.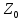 .
. )
a+1=a’
; 2.(
)
a+1=a’
; 2.(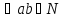 )
a+b’=(a+b)’)
и теорему 1(сложение (умножение) N
чисел существует и оно единственно),
составим таблицу сложения однозначных
N
чисел:
)
a+b’=(a+b)’)
и теорему 1(сложение (умножение) N
чисел существует и оно единственно),
составим таблицу сложения однозначных
N
чисел: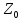 чисел считают, что для любого (
чисел считают, что для любого (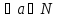 )
a-0=a/
)
a-0=a/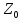 чисел изменяется условие существования
разности: чтобы существовала разность
чисел изменяется условие существования
разности: чтобы существовала разность
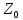 чисел а и б необходимо и достаточно,
чтобы было б
чисел а и б необходимо и достаточно,
чтобы было б а.
а.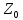 .
Формулировка правил деления суммы,
разности и произведения на число.
.
Формулировка правил деления суммы,
разности и произведения на число. ,
что a=bq+r , причём 0<r<b.
,
что a=bq+r , причём 0<r<b. Nчисел
a
и b
существуют
Nчисел
a
и b
существуют
 q
и r
такие, что a=bq+r, причём 0<r<b.
Другой пары
q
и r
такие, что a=bq+r, причём 0<r<b.
Другой пары
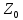 (q
и r)
c
тем же свойством не существует.
(q
и r)
c
тем же свойством не существует.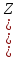 ).
).
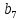 либо а<б либо а>б
либо а<б либо а>б и из того, что оно истинно для n=K’,
то утверждение A(n)
– истинно для любого N
числа n.
и из того, что оно истинно для n=K’,
то утверждение A(n)
– истинно для любого N
числа n.
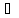 М;
2) k
М;
2) k 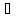 M
M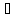 M.
Отсюда, на основании аксиомы 4, заключаем,
что М
= N,
т.е. утверждение А(n) истинно
для любого натурального n.
Метод доказательства, основанный на
этой теореме, называется методом
математической индукции. Такое
доказательство состоит из двух частей:
1) доказывают, что утверждение А(n) истинно
для n
= 1,
т.е. что истинно высказывание А(1);
2) предполагают,
что утверждение А(n) истинно
для n
= k,
и, исходя из этого предположения,
доказывают, что утверждение A(n) истинно
и для n
= k + 1,
т.е. что истинно высказывание A(k)
M.
Отсюда, на основании аксиомы 4, заключаем,
что М
= N,
т.е. утверждение А(n) истинно
для любого натурального n.
Метод доказательства, основанный на
этой теореме, называется методом
математической индукции. Такое
доказательство состоит из двух частей:
1) доказывают, что утверждение А(n) истинно
для n
= 1,
т.е. что истинно высказывание А(1);
2) предполагают,
что утверждение А(n) истинно
для n
= k,
и, исходя из этого предположения,
доказывают, что утверждение A(n) истинно
и для n
= k + 1,
т.е. что истинно высказывание A(k) 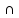 А(k)
А(k)  )
то есть 0=n(
)
то есть 0=n( )
)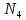 =
=
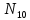 т.к
чтобы определить число соответствующее
множеству А прибегают к счету, а для
этого нужны некоторые отрезок N
ряда.
т.к
чтобы определить число соответствующее
множеству А прибегают к счету, а для
этого нужны некоторые отрезок N
ряда.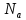 ,
где a-
называется число элементов во мн А и
записывается n(A)=a.
Полученное a
в этом смысле называется количественное
N
число. Порядковые
N
числа выражаются числительными
(первый, второй). При счёте числа
обладают рядом свойств: располагаются
в определенном порядке, должно
существовать первое число и т.п
,
где a-
называется число элементов во мн А и
записывается n(A)=a.
Полученное a
в этом смысле называется количественное
N
число. Порядковые
N
числа выражаются числительными
(первый, второй). При счёте числа
обладают рядом свойств: располагаются
в определенном порядке, должно
существовать первое число и т.п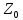 ).
).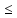 а
а х
х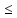 б,
а это значит что при а<б отрезок
б,
а это значит что при а<б отрезок
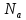 это подмножество
это подмножество
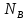 (беттое)
и обратное если,
(беттое)
и обратное если,
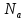 -
собственное подмножество
-
собственное подмножество
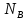 ,
то а<б.
,
то а<б.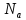 является собственным подмножеством
отрезка
является собственным подмножеством
отрезка
 .
. и подмножеством отрезка ряда
и подмножеством отрезка ряда
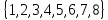 то есть
то есть
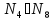 .
. B,
B
B,
B C
C
 A
A C
C B,
то B
B,
то B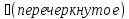 А.
А. N
вытесняет из того, что
N
вытесняет из того, что
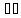 в любой отрезок
в любой отрезок
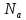 (
(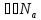 )
) .
Теорема: Пусть А - конечное множество
и B
его собственное подмножество, тогда
мн A\B
тоже конечно, причём выполняется
равенство n(A\B)=n(A)-n(B).
С теоретико-множественной позиции
разность N
чисел a
и b
представляет
собой число элементов в дополнении
подмножества B
до мн A,
если : a=n(A),
b=n(B),
то B
явл.подмножеством A:
a-b=n(A)-n(B)=n(A\B),
a-0=a:n(A\
.
Теорема: Пусть А - конечное множество
и B
его собственное подмножество, тогда
мн A\B
тоже конечно, причём выполняется
равенство n(A\B)=n(A)-n(B).
С теоретико-множественной позиции
разность N
чисел a
и b
представляет
собой число элементов в дополнении
подмножества B
до мн A,
если : a=n(A),
b=n(B),
то B
явл.подмножеством A:
a-b=n(A)-n(B)=n(A\B),
a-0=a:n(A\ )=n(A)=a,
a-a=0::n(A\A)=n(
)=n(A)=a,
a-a=0::n(A\A)=n( )=0.
С т-м позиции a<b
на с
или
(b>a
на c)
означает, что если а=n(A),
а b=n(B),
то в мн В содержится столько же
элементов, сколько в мн А и еще с
элементов. Взаимосвязь действий над
множествами с действиями над числом
и т-м смысл отношений «меньше на» и
«больше на» позволяют обосновать
выбор действий при решении задач с
этими отношениями. Пример: на столе 5
чашек, а ложек на 2 меньше. Сколько на
столе ложек? 2 мн: чашки(А) и ложки (В).
n(B)=n(A)-2=5-2-3
)=0.
С т-м позиции a<b
на с
или
(b>a
на c)
означает, что если а=n(A),
а b=n(B),
то в мн В содержится столько же
элементов, сколько в мн А и еще с
элементов. Взаимосвязь действий над
множествами с действиями над числом
и т-м смысл отношений «меньше на» и
«больше на» позволяют обосновать
выбор действий при решении задач с
этими отношениями. Пример: на столе 5
чашек, а ложек на 2 меньше. Сколько на
столе ложек? 2 мн: чашки(А) и ложки (В).
n(B)=n(A)-2=5-2-3 B)=n(A)*n(B).
B)=n(A)*n(B).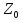 ,
есть число элементов в Декартовом
произведении множеств A
и B
таких, что а=n(A),
б=n(B),
a*б=n(A
,
есть число элементов в Декартовом
произведении множеств A
и B
таких, что а=n(A),
б=n(B),
a*б=n(A B)=n(A)*n(B).
B)=n(A)*n(B).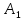 )=n(
)=n( )=n(
)=n(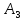 )=4
)=4 )=4+4+4=4*3=12
)=4+4+4=4*3=12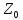 ,
то a*b
называется числом, удовлетворяющим
следующим условиям: 1) а*b=a+a+….a,
где a+a+….a
используется b
раз и b>1.
2) a*b=a,
если b=1.
3)a*b=0,
если b=0.
Свойству
1 из определения можно дать следующую
т-м трактовку: если мн
,
то a*b
называется числом, удовлетворяющим
следующим условиям: 1) а*b=a+a+….a,
где a+a+….a
используется b
раз и b>1.
2) a*b=a,
если b=1.
3)a*b=0,
если b=0.
Свойству
1 из определения можно дать следующую
т-м трактовку: если мн
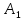 ,
,
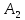 …
…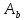 содержит по а
элементов
каждое, причём никакие 2 из них не
пересекаются, то их объединение
содержит по а
элементов
каждое, причём никакие 2 из них не
пересекаются, то их объединение
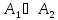 …
…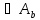 содержит a*b
элементов. С т-м позиции произведение
a*b
при
b>1
представляет
собой число элементов в объединении
B
множеств, каждое из которых содержит
по a
элементов и никакие 2 из них не
пересекаются. a*b=n(
содержит a*b
элементов. С т-м позиции произведение
a*b
при
b>1
представляет
собой число элементов в объединении
B
множеств, каждое из которых содержит
по a
элементов и никакие 2 из них не
пересекаются. a*b=n( …
… ,
если n(
,
если n(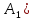 =n(
=n(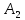 )…n(
)…n(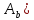 =a
и каждое из них попарно не пересекаются.
=a
и каждое из них попарно не пересекаются. а
= с·b
Итак, во втором случае частное
определено через произведение. Поэтому
говорят, что деление есть действие,
обратное умножению.
Всегда ли
существует частное натуральных чисел
a и b? Ответ на этот вопрос дает следующая
теорема:
Теорема.
Для того чтобы существовало частное
двух натуральных чисел а и b, необходимо,
чтобы b≤а.
Доказательство.
Пусть частное натуральных чисел a и b
существует, т. е. существует такое
натуральное число с, что а = с·b. Для
любого натурального числа с справедливо
утверждение 1≤с. Умножим обе части
этого неравенства на натуральное
число b, получим b≤c·b. Поскольку с·b =
а, то b≤а. Теорема доказана.
Чему
равно частное, а = 0 и натурального
числа b? По определению это такое число
а, которое удовлетворяет условию с·b
= 0. Так как b ≠ 0, то равенство c·b = 0 будет
выполняться при с = 0. Следовательно,
0:b = 0, если b
а
= с·b
Итак, во втором случае частное
определено через произведение. Поэтому
говорят, что деление есть действие,
обратное умножению.
Всегда ли
существует частное натуральных чисел
a и b? Ответ на этот вопрос дает следующая
теорема:
Теорема.
Для того чтобы существовало частное
двух натуральных чисел а и b, необходимо,
чтобы b≤а.
Доказательство.
Пусть частное натуральных чисел a и b
существует, т. е. существует такое
натуральное число с, что а = с·b. Для
любого натурального числа с справедливо
утверждение 1≤с. Умножим обе части
этого неравенства на натуральное
число b, получим b≤c·b. Поскольку с·b =
а, то b≤а. Теорема доказана.
Чему
равно частное, а = 0 и натурального
числа b? По определению это такое число
а, которое удовлетворяет условию с·b
= 0. Так как b ≠ 0, то равенство c·b = 0 будет
выполняться при с = 0. Следовательно,
0:b = 0, если b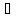 N.
Теорема.
Если частное натуральных чисел а и b
существует, то оно единственно
N.
Теорема.
Если частное натуральных чисел а и b
существует, то оно единственно ,
,
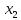 ,…,
,…,
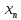 ,
если он является их объединением и
никакие два из них не имеют общих
внутренних точек, хотя и могут иметь
общие концы.
,
если он является их объединением и
никакие два из них не имеют общих
внутренних точек, хотя и могут иметь
общие концы.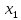 ,
,
 ,…,
,…,
 и пишут х =
и пишут х =
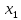 +О
+О
 +О
+О
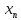
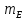 (Х).
(Х).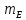 (Х).
(Х).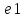 => отрезок а
будет составлен из pq отрезков
=> отрезок а
будет составлен из pq отрезков
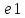 ,
т.к. каждый отрезок e составлен из q
,
т.к. каждый отрезок e составлен из q
 ,
всего отрезков ep => me1a
= q+q+…+q=pq. Вывод: при переходе к более
мелкой единице измерения, вычисляя
меру отрезка а
при новой единице измерения выполняется
действие умножения, т.е умножение N
чисел отражает переход к новой единице
длины: если N
число p
мера отрезка а
при единице длины е,
а N
число q
мера отрезка е
при единице длины
,
всего отрезков ep => me1a
= q+q+…+q=pq. Вывод: при переходе к более
мелкой единице измерения, вычисляя
меру отрезка а
при новой единице измерения выполняется
действие умножения, т.е умножение N
чисел отражает переход к новой единице
длины: если N
число p
мера отрезка а
при единице длины е,
а N
число q
мера отрезка е
при единице длины
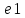 ,
то произведение pq
является мерой отрезка а
при единице длины
,
то произведение pq
является мерой отрезка а
при единице длины
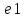 .Пусть
a=b+c,
mea
=p,
meb
= q,
тогда mec
= p-q.
Вывод: разность 2х натуральных чисел
p
и
q,
где p
мера отрезка а
при единице длины е,
а q
мера отрезка b
при единице длины е = mec,
которая является дополнением отрезка
b
до отрезка а.
mea=p,
mee1=q,
me1a=p:q.
Вывод: операция деления натуральных
чисел отражает переход новой единицы
длины к более крупной: если p
это мера отрезка а
при единицы длины е, а q
это мера отрезка е1 при единице длины
е,
то мера отрезка а
при единице длины е1 =p:q.
.Пусть
a=b+c,
mea
=p,
meb
= q,
тогда mec
= p-q.
Вывод: разность 2х натуральных чисел
p
и
q,
где p
мера отрезка а
при единице длины е,
а q
мера отрезка b
при единице длины е = mec,
которая является дополнением отрезка
b
до отрезка а.
mea=p,
mee1=q,
me1a=p:q.
Вывод: операция деления натуральных
чисел отражает переход новой единицы
длины к более крупной: если p
это мера отрезка а
при единицы длины е, а q
это мера отрезка е1 при единице длины
е,
то мера отрезка а
при единице длины е1 =p:q.