Московский Государственный Университет Геодезии и Картографии

Утверждаю

Проректор по УР __________

МаксудоваЛ.Г.

Перечень вопросов

государственного экзамена по специальности

"Информационные системы"

(специализациия «ГИС» и «Телекоммуникации»)

Москва

2012 г.

Составители: Гаврилова В.В., Шавенько Н.К. Перечень вопросов государственного экзамена по специальности "Информационные системы"(специализации «ГИС» и «Телекоммуникации»). МИИГАиК, 2012 г.

Методические указания «Перечень вопросов государственного экзамена по специальности "Информационные системы"(специализация «ГИС» и «Телекоммуникации») составлены в соответствии с утвержденной Программой государственного экзамена и предназначены для студентов 5 курса факультета « Прикладной космонавтики и фотограмметрии» в помощь при подготовке к сдаче Государственного экзамена.

© Московский государственный университет

геодезии и картографии, 2012.

I. Обработка геопространственных данных

1.1. Дискретная математика и анализ данных. (Кафедра вТиАоаи)

1. Множества, подмножества и операции над ними. Логические переменные и операции над ними. Описание операций над множествами с помощью логических операций.

Одним из неопределяемых понятий в математике является «множество». Этому понятию нельзя дать формального определения, которое не сводилось бы к просто к замене слова «множество» его синонимами «совокупность», «набор элементов» и т.д. Множества можно составлять на основе самых различных признаков из самых различных объектов (которые в дальнейшем будем именовать элементами множества).множество можно задать, указывая, например, некоторое свойство объектов, образующих множество, правило построения элементов множества и т.д.

Множества чаще всего обозначаются прописными буквами латинского алфавита: А,В,…..Х, а их элементы – строчными буквами: а, в, ….,х.

2 множества равны, если они состоят из одних и тех же элементов:

А={2,2,0,1,1}

A={2,0,1}

Множества, не состоящие не из одного элемента – пустые множества.

 - пустое множество.

={}

Множество, состоящее из элементов другого множества – подмножество данного множества.

А={0,3,1}

B={3,1}

ВА

Любое пустое множество является подмножеством любого множества.

Множества могут быть конечными и бесконечными.

Множество, эквивалентное отрезку натурального ряда, называется конечным множеством (пустое множество тоже является конечным множеством).

Если множество конечное, то можно ввести понятие мощность множества (равна конечному числу его элементов).

|A|

Множество, не являющееся конечным, называется бесконечным.

Счетное множество – множество, каждому элементу которого можно поставить в соответствие элемент из натурального ряда чисел. Счетное множество – это бесконечное множество, элементы которого можно «перенумеровать» при помощи множества натуральных чисел, т.е. можно указать такой способ нумерации элементов множества, при котором каждый элемент множества получит свой единственный номер.

Свойства бесконечных множеств.

всякое подмножество счетного множества конечно или счетно.

сумма любого конечного или счетного множества счетных множеств есть счетное множество.

всякое бесконечное множество содержит счетное подмножество.

2 Множества равны, если они состоят из одних и тех же элементов.

А={а,а,в,с,в}={а,в,с}

|A|=3

Множество ВА, если В={В/вВвА}

2 свойства подмножеств.

любое пустое множество является подмножеством данного множества.

множество является подмножеством самого себя.

Универсальное множество – множество, по отношению к которому все остальные множества, формируемые для решения конкретной задачи или для конкретной области применения, является подмножеством данного множества.

Степень множества – множество всех подмножеств данного множества:

QA={Ai/AiA}- степень множества А.

|QA|=2n

QA(p)={Ai/A |Ai| =p }- Множество всех подмножеств А, у которого мощность равна р.

|QA(p)|=Cnp=

Операции над множествами.

Объединение. Объединением двух множеств называется множество, состоящее из всех элементов, принадлежащих хотя бы одному из этих множеств.

A{X/XA XB }

Пересечение. Пересечением двух множеств называется множество, состоящее из всех элементов, принадлежащих одновременно обоим множествам.

A{X/XA XB }

Разность между А и В. A\B={X/XA XB }

{X/X XA}- дополнение к множеству А.

 - универсальное множество.

Свойства операций над множествами.

Коммутативность.

А В=В А, А В=ВА

Ассоциативность.

(А В) С=А (В С)

(А В) С= А (В С)

Дистрибутивность.

А (В С)=(А В) (В С)

А (В С)=(А В) (В С)_

Закон де Моргана.

Идемпотенция.

Логические переменные. Операции над ними.

Результат утверждения, сформулированного в повествовательной форме, при котором:

1, если утверждение верно(истинно)

Р=

0, если утверждение ложно

Р - результат.

Р ={0,1}

а*в=с -бинарные операции.

а, в – операнды.

* - операция

с – результат операции.

Бинарные операции.

1. - логическое сложение

2 . - логическое умножение

3. а­­­­­­­­ b – отрицание

с помощью двух бинарных операций и одной одноместной можно получить 16логических операций.

4 . Штрих Шеффера

a/b= a­­­­­­­ b –разность

Старшинство операций.

Скобки.

Логическое отрицание.

Логическое умножение.

Логическое сложение.

Свойства логических операций.

Коммутативность.

Ассоциативность.

Дистрибутивность.

Свойство максимального элемента.

1a=1

0a=0

Упорядоченное множество. Кортеж.

А ={a_i}={a₁ a₂…….. a_n}

Последовательность элементов принадлежащих А, расположенных в строго заданном порядке.

Если элементы кортежа являются элементами численного множества, то такой кортеж принято называть вектором, а сами элементы этого кортежа – компонентами.

2. Модели измерений. Фундаментальная система измерений и их решения. Анализ ошибок измерений.

Н аблюдения измерения

Подсчет

Измерения обязательно связаны с о сравнением измеряемой величины с эталоном.

Измерения бывают:

-прямые

-косвенные.

Прямое измерение – интересующий параметр получается непосредственно в процессе измерений.

Косвенное измерение – измеряется функция от измеряемой величины.

Измерительная система является сложной системой:

Объект измерения

Канал связи

Датчик сигнала

Датчик сигналов

Измерительное устройство

Результат первого измерения

Шум

Результат первичных измерений

Система обработки измерений

Результат измерения

Ошибки вычисления, округления

Шум

Измерительная система

Q_k X_i

измеряемый измеряемая величина

параметр

_i

 ₁(Q₁ Q₂ Q_k Q_m) = x₁-₁

₂(Q₁ Q₂ Q_k Q_m) = x₁-₂ (*)

_n(Q₁ Q₂ Q_k Q_m) = x₁-₃

Перепишем в виде: - Фундаментальная система измерений.

- данные измерения - известны

- оператор измерительной системы, для данного подхода – известен.

- не известны.

В (*) имеется (m+n) – неизвестных.

Известен закон распределения ошибок. Будем считать, что ошибки отсутствуют. Поэтому, система превращается в , где m- неизвестных и n- уравнений.

Систему можно решить, если m=n, т.е. число измерений – минимальное.

- в общем случае нелинейная.

Поэтому имеется 2 метода решения:

-прямой

-итерационный.

Прямой – метод, в результате которого получаются точные решения при отсутствии ошибок округления.

Итерационный – метод, в результате применения которого получается приближенное решение, поэтому обычно рассматриваются только сходящиеся итерационные процессы, в результате применения которого, можно получить результат с любой заданной точностью независимо от задания начальных условий (при отсутствии ошибок округления).

В ряде случаев итерационный процесс может привести к более точным результатам, т.к. отсутствуют ошибки.

Итерационный метод используется для начальных инженерных расчетов.

Любой итерационный процесс начинается с задания начальных условий.

Рассмотрим решение этой задачи в общем виде, т.е. 0.

Пусть ₀- известен (начальное значение). ₀ такое, что ₁…_n можно разложить в ряд Тейлора в окрестности ₀ с точностью до второго порядка малости.

О₂=² – малая величина.

Пусть

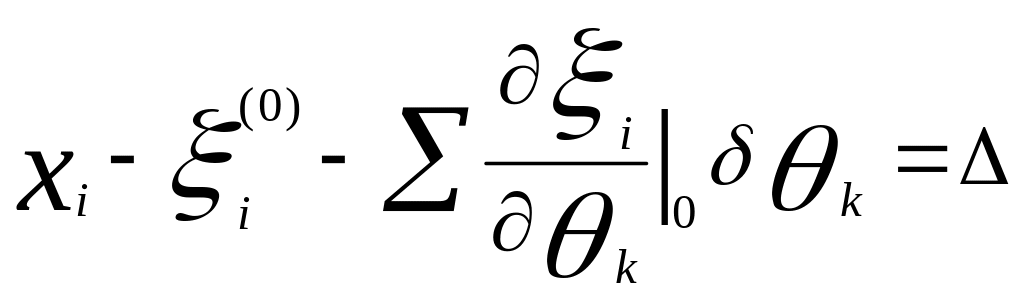
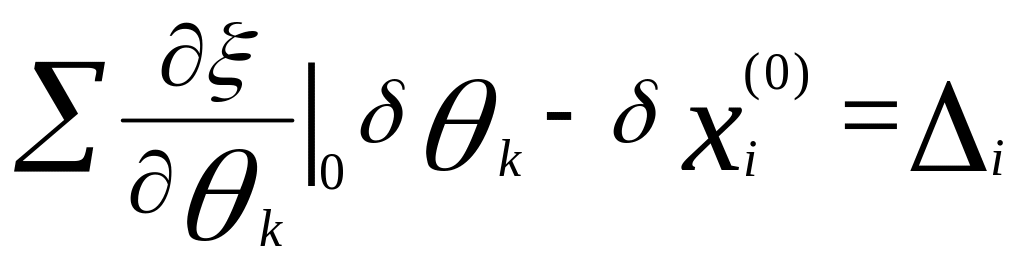
- уравнение поправок ( (0)- для начальной итерации)

Таким образом, получили систему уравнений, у которой:

- неизвестно

- неизвестно

m+n – неизвестных

m - уравнений

Надо сделать, чтобы:

m<n

min

- вектор невязок

Пусть G_q=E, тогда решаем систему по методу наименьших квадратов:

- (*) – нормальная система уравнений.

Таким образом, свели общую задачу к нормальной системе уравнений.

Найдем из нормальной системы уравнений

Подставляем найденное решение в исходящую систему и определяем величину невязки ( ).

Нам был задан >0. Проверяем условие , если выполняется , то , не выполняется.

За принимаем , т.е. , далее и переход на (*).

Получаем:

,

традиционный метод решения уравнения поправок по методу наименьших квадратов.

3. Операторные уравнения. Нахождение псевдорешения. Обусловленность СЛАУ.

Операторные уравнения.

Пусть А – оператор, действующий из m – мерного линейного пространства Х в n – мерное линейного пространство Y, заданных над одним и тем же полем Р. Определим все векторы хХ, которые при заданных операторе А и векторе уY удовлетворяют уравнению:

Ах = у.

Это уравнение называется операторным уравнением, вектор х – его решением, а вектор у – правой частью.

Решение СЛАУ по методу наименьших квадратов.

Теорема:

Для любого операторного уравнения Ах = у имеется решение по методу наименьших квадратов Х, удовлетворяющее равенству:

Доказательство:

Докажем :

Пусть Т – область значения оператора А, тогда Т Y, причем T = Y  m=n=Rg A. В Т найдется элемент u0 Т, для которого выполняется равенство:

(символ inf обозначает наименьшее значение и называется наилучшим решением операторного уравнения).

При этом для элемента и0 и любого элемента и Т должно выполняться условие:

,

которое в нашем случае примет вид:

Отсюда

Т. к. это равенство выполняется для любых хХ, то получаем .

Докажем, что всегда найдется:

Это равносильно тому, что операторное уравнение разрешимо. Рассмотрим скалярное произведение между правой частью уравнения и любым вектором v ker A*A. С учетом того, что ker A = ker A*A имеем:

Но т. к. А*Аv=0, то и (А*Аv)=0 и на основании теоремы Фредгольма (операторное уравнение разрешимо тогда и только тогда, когда его правая часть ортогональна всем решениям сопряженного однородного уравнения) получаем, что уравнение разрешимо.

При произвольно заданных базисах в евклидовых пространствах X и Y уравнение представляется в виде системы линейных алгебраических уравнений которая имеет следующую форму записи:

,

после преобразований получаем: - нормальная система уравнений,

где Gq – матрица Грамма для системы базисных векторов в пространстве Y. Для случая, когда в Y задана ортонормированная система базисных векторов, Gq=Е и .

Выражение Ах – у = v – называется системой уравнений поправок.

Вектор решения системы нормальных уравнений называется псевдорешением уравнений поправок.

Т.к. нормальная система уравнений совместная, то она имеет или единственное решение, или множество решений.

Когда Rg A = m, где m – размерность пространства Х, псевдорешение единственно:

,

когда же Rg A < m, то нормальная система уравнений имеет множество решений.

Если решение нормальной системы уравнений не единственно, то при отсутствии какой – либо дополнительной информации о решении системы уравнений поправок, которая, как правило, может быть получена из физической сущности задачи или по дополнительным измерениям, за ее решение берется псевдорешение наименьшей длины, называемое нормальным псевдорешением:

Метод простой итерации.

Если требуется найти приближенные решения системы Ах = b методом простой итерации, то сначала исходную систему приводим к эквивалентной системе вида: х = Сх + d.

Затем по заданному значению х(0) (начальное приближение) вычисляем первое приближенное значение по формуле:

,

потом второе приближенное значение по формуле:

,

т. е. в общем виде:

(*) , где С – матрица.

Т.о. вычислительный процесс, основанный на решении систем по формуле (*), называется методом простой итерации.

Чтобы прервать итерационный процесс:

наложить ограничение на число итераций,

наложить ограничение на , где  - точность, т.е. если решение обладает уже заданной точностью.

! Алгоритм обязательно должен быть сходящимся.

Достаточное условие сходимости метода простой итерации: .

Для сходимости метода простой итерации необходимо и достаточно, чтобы наибольшее по модулю собственное значение матрицы С было меньше 1: sup

Итерационный метод Зейделя.

А[nxn]: Ax = b  x = cx + d  x = c₁x + c₂x + d, где с = с₁ + с₂

(*) x^(к+1) = c₁x^(к+1)+ c₂x^(к) + d – итерационный метод Зейделя

х⁽⁰⁾ – задана

x⁽¹⁾ = c₁x⁽¹⁾+ c₂x⁽⁰⁾ + d

(Е – с₁)х⁽¹⁾ = c₂x⁽⁰⁾ + d = =>

метод Зейделя в матричном виде.

Метод Зейделя в координатном виде:

x = cx + d в координатной форме:

……………………………………

В методе простой итерации:

……………………………………………….

В общем виде:

…………………………………………………

Число операций умножения:

- в методе простой итерации

- в методе Гаусса,

если , то метод простой итерации сходится быстрее, чем метод Гаусса.

В методе Зейделя:

………………………………………………

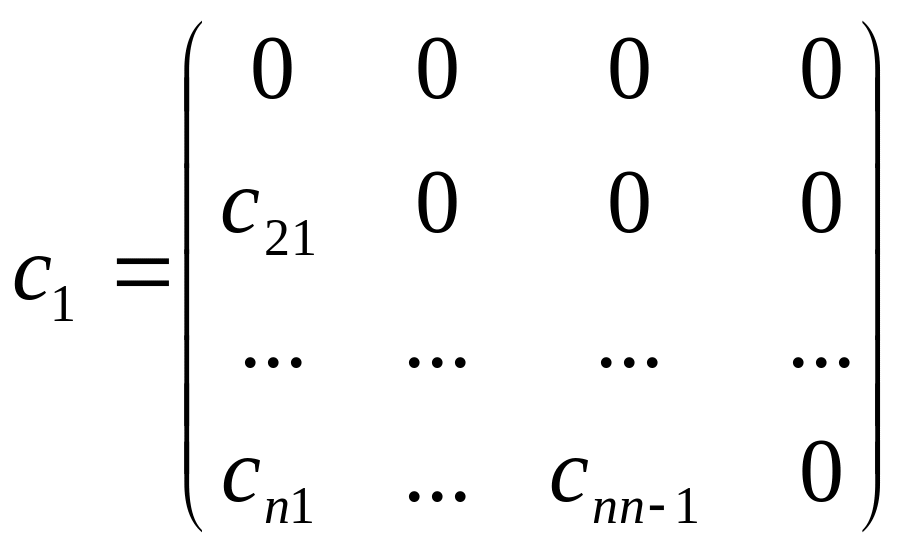
Проблемы метода Зейделя:

Сходиться ли итерационный процесс? Условия сходимости.

И з (*) => (Е – с₁)х^(k+1) = c₂x^(k) + d

никогда не будет

вырожденной

х ^(к+1) = (Е – с₁)^-1* c₂x^(k) + (Е – с₁)^-1* d

М f

х^(к+1) = М x^(k) + f => условия сходимости метода Зейделя = условиям сходимости метода простой итерации.

Условия сходимости метода простой итерации (и метода Зейделя):

Оценка точности:

Погрешность (ошибка):

Сравнение метода простой итерации и метода Зейделя:

Одинаковы по занимаемой памяти.

Одинаковы по точности (можно задать).

Различная скорость сходимости:

из сходимости метода простой итерации не следует сходимости метода Зейделя, и наоборот,

скорость сходимости различная и зависит от матриц.

4. Общий подход к приближению функций. Интерполяция по Лагранжу. Метод Ньютона для разделенных разностей. Интерполяция сплайнами.

Интерполяция, аппроксимация функций, общая постановка задачи.

Приближение функций (ПФ).

Основные области применения ПФ:

Моделирование, описание поверхностей (рельефа).

Решение инженерных задач по этим моделям (подсчет площади, определение границ и т.д.).

Сжатие данных.

Обработка снимков и карт.

Методы решения этих задач с помощью ПФ:

Приближение функций