
- •080100.62 По направлению Экономика
- •Понятие функции двух независимых переменных
- •2. Производные функции двух независимых переменных
- •2.1. Частные производные первого порядка
- •2.2. Частные производные высших порядков
- •3. Полный дифференциал функции двух переменных
- •4. Касательная плоскость и нормаль к поверхности
- •5. Экстремум функции двух независимых переменных
- •5.1. Необходимое условие экстремума
- •5.2. Достаточные условия экстремума
- •6. Градиент и производная по направлению
- •7. Метод наименьших квадратов
- •8. Первообразная и неопределенный интеграл
- •Свойства интегралов
- •9. Методы интегрирования
- •9.1. Непосредственное интегрирование
- •9.2. Метод замены переменной (подстановки)
- •9.3. Метод интегрирования по частям
- •10. Интегрирование рациональных дробей
- •10.1. Простейшие дроби, их интегрирование к простейшим дробям относятся дроби вида:
- •10.2. Правильные и неправильные рациональные дроби
- •10.3. Разложение правильной дроби
- •10.4. Нахождение коэффициентов
- •10.5. Правило интегрирования рациональных дробей
- •11. Интегрирование некоторых иррациональностей
- •12. Интегрирование тригонометрических выражений
- •13. Определенный и несобственный интегралы, их вычисление
- •14. Геометрические приложения определенного интеграла
- •Из чертежа видно, что
9.3. Метод интегрирования по частям
 (20)
(20)
Эта
формула чаще всего применяется тогда,
когда под интегралом имеется произведение
алгебраической и трансцендентной
функции, например,
 или
или
 ,
,
 или
или
 .
.
 – это все подынтегральное выражение,
часть которого мы обозначаем за
– это все подынтегральное выражение,
часть которого мы обозначаем за
 ,
а часть за
,
а часть за
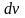 .
При этом:
.
При этом:
за принимается функция, которая дифференцированием упрощается.
за – та часть, интеграл от которой известен или легко может быть взят.
в состав обязательно входит
 .
.
В итоге верного выбора и интеграл в (20) должен быть проще исходного.
Пример
25.

 .
.
Замечание. Метод интегрирования по частям может применяться в одном примере несколько раз.
Замечание.
Иногда повторное интегрирование по
частям приводит к уравнению искомого
интеграла
 ,
,  ,
если
,
если
 ,
то получаем уравнение:
,
то получаем уравнение:
 ,
откуда
,
откуда
 или
или
 .
.
Пример
26.
 – решить методом по частям, используя
примечание. При верном решении должен
получиться ответ:
– решить методом по частям, используя
примечание. При верном решении должен
получиться ответ:
 .
.
Только по частям берутся интегралы:
а)
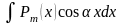 ,
,
 многочлен
многочлен
 -ой
степени,
-ой
степени,
 ,
в частности одночлен
,
в частности одночлен
 ,
,
 ,
,
б)
 ,
,
 ,
,
 ,
,
 ,
,
 ,
,
в)
 ,
,
 ,
,  ,
,
 ,
,
 или
или  .
.
Интегралы типа (в) интегрируются дважды по частям.
Пример
27.
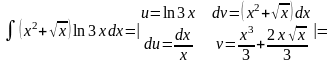

 .
.
Рассмотрим отдельные классы функций и способы их интегрирования.
10. Интегрирование рациональных дробей
10.1. Простейшие дроби, их интегрирование к простейшим дробям относятся дроби вида:
1.
 , 2.
, 2.
 , 3.
, 3.
 , при
, при
 ,
,
4.
 ,
при
(
,
,
,
,
при
(
,
,
,
 ,
,
 ,
,
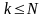 ).
).
При
интегрировании дробей типа 1 – 2 достаточно
ввести подстановку
 ,
,
 (или
(или
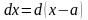 ),
тогда
),
тогда
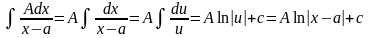 ;
; ,
(
).
,
(
).
Чтобы проинтегрировать дроби типа 3 – 4, необходимо выделить полный квадрат из квадратного трехчлена, затем свести интеграл к табличному.
Пример
28.
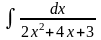 .
.
Решение. Выделим полный квадрат из квадратного трехчлена:
 .
.
 =
=

(табл. интегр., 11).
Замечание. При интегрировании дробей типа 3 – 4 можно воспользоваться справочником.
10.2. Правильные и неправильные рациональные дроби
Определение
13. Дробь
 называется рациональной, где
называется рациональной, где
 ,
,
 – многочлены
-ой
и
– многочлены
-ой
и
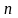 -ой
степеней.
-ой
степеней.
Если
 ,
дробь неправильная.
,
дробь неправильная.
Если
 ,
дробь правильная.
,
дробь правильная.
Неправильную дробь представляют в виде суммы целой части и правильной дроби. Операция выделения целой части может быть выполнена делением числителя на знаменатель.
Пример
29. Дробь
 неправильная (
неправильная ( ,
,
 ,
,
 ).
Выделим целую часть, разделив числитель
на знаменатель.
).
Выделим целую часть, разделив числитель
на знаменатель.




 .
.



Пример
30. Дробь
 правильная, т. к.
,
правильная, т. к.
,
 ,
.
,
.
Пример
31. Дробь
 неправильная (
неправильная ( ,
,
 ,
,
 ).
).





 .
.
10.3. Разложение правильной дроби
Теорема. Всякая правильная рациональная дробь может быть представлена в виде суммы конечного числа простейших дробей вида 1 – 4.
Пусть
дробь
 правильная. Разложим знаменатель дроби
на множители. Найдем его корни, т. е.
значения
,
при которых знаменатель обращается в
нуль. Тогда многочлен
разложится на множители:
правильная. Разложим знаменатель дроби
на множители. Найдем его корни, т. е.
значения
,
при которых знаменатель обращается в
нуль. Тогда многочлен
разложится на множители:
 ,
где
,
где
 – действительные
корни многочлена. Множитель
– действительные
корни многочлена. Множитель
 не разложим на линейные множители, т.
к.
.
не разложим на линейные множители, т.
к.
.
Вид элементарной дроби и число их в разложении определяется корнями знаменателя данной дроби. Каждому множителю знаменателя соответствует определенного вида дробь. Укажем, какому множителю какая дробь соответствует:


 ,
если
.
,
если
.
 ,
,
если .
 – пока неизвестные коэффициенты.
– пока неизвестные коэффициенты.
Разложить на простейшие дроби.
Пример
32.
 .
.
Пример
33.


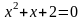 – не
имеет действительных корней, т. к.
– не
имеет действительных корней, т. к.
 .
.
Пример
34.

 .
.
Пример
35.

 ,
,
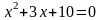 – не
имеет действительных корней, т. к.
.
– не
имеет действительных корней, т. к.
.
