Експоненційний закон розподіл

Експонеційний закон розподілу відіграє велику роль в теорії масового обслуговування та теорії надійності.

Безперервна випадкова величина X має експоненційний закон розподілу з параметром , якщо її щільність ймовірності f(x) має вигляд:

На рис 1.8 показано графік щільність розподілу ймовірності експоненційного закону розподілу.

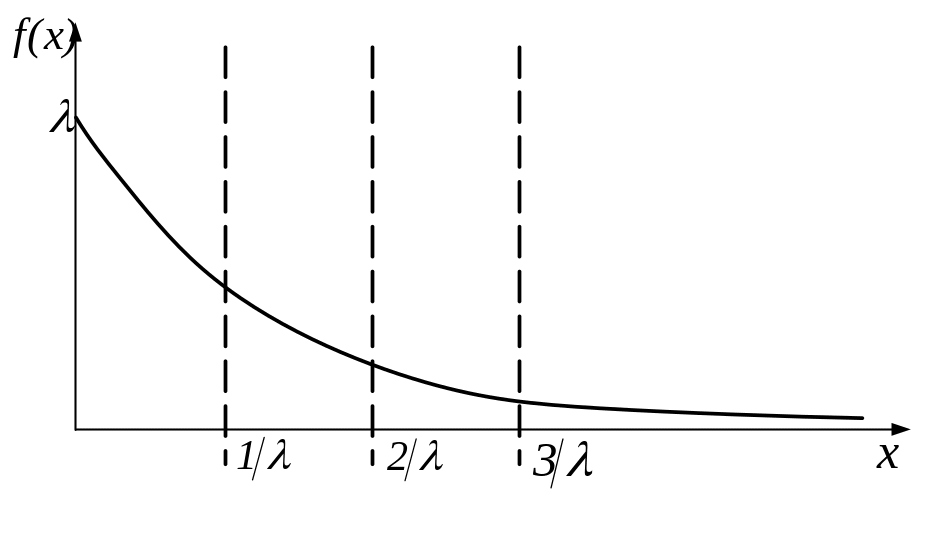
Рис. 1.8 Графік щільності розподілу ймовірності еспоненційного закону

Функція розподілу випадкової величини X, розподіленої по експоненційному закону, є

Графік функції F(х) наведений на рис 1.9.

Визначимо числові характеристики випадкової величини з рівномірним розподілом.

Математичне очікування

Дисперсія

Середньоквадратичне відхилення

Коефіцієнт асиметрії

.

Ексцес дорівнює

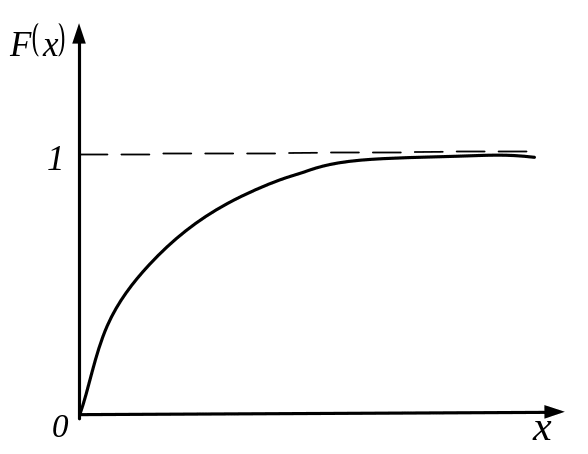
Рис. 1.9. Графік функції розподілу експоненційного закону

Релеевський закон розподілу

Безперервна випадкова величина X має релеевський закон розподілу з параметром , якщо її щільність ймовірності f(x) має вигляд:

,

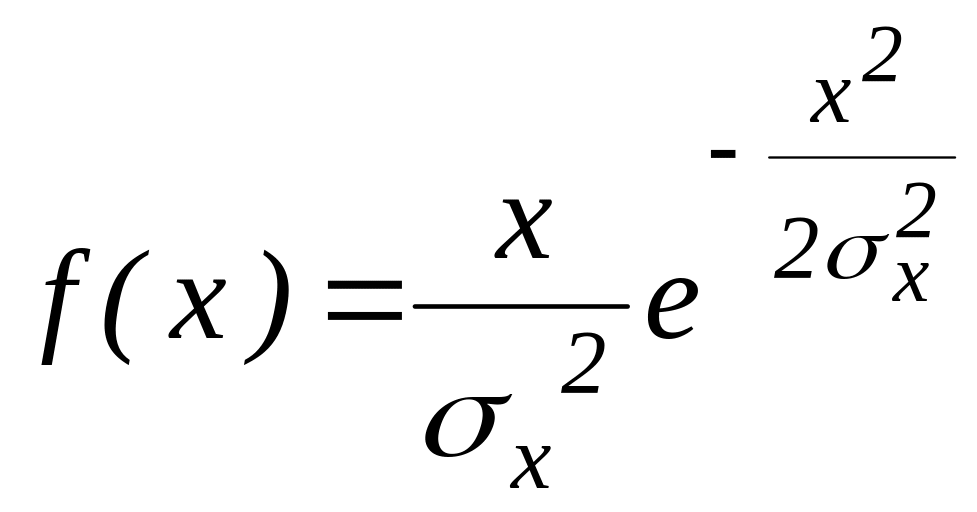На рис 1.10 показано графік щільності розподілу ймовірності релевського закону розподілу.

Функція розподілу випадкової величини X, розподіленої по релеевському закону, є

,

Графік функції F(х) наведений на рис 1.11.

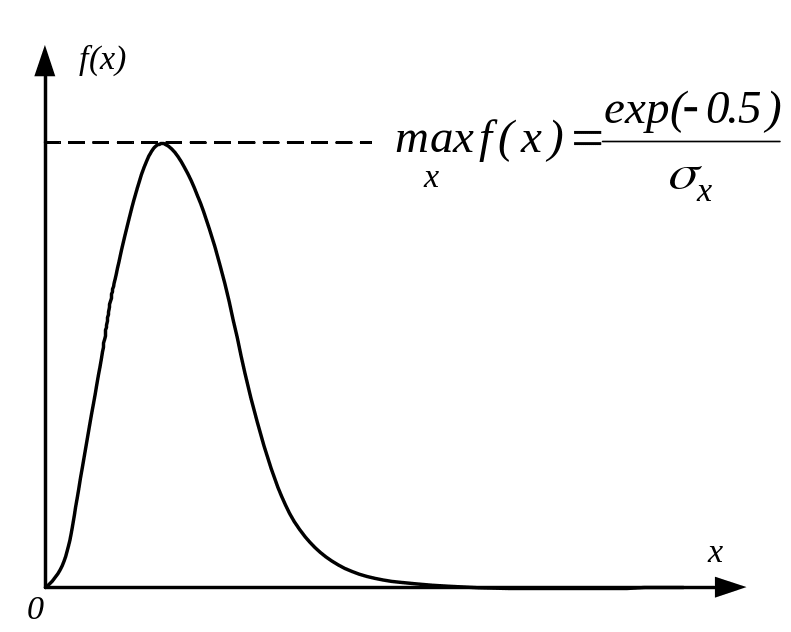
Рис. 1.10 Графік щільності розподілу ймовірності релеевського закону

Рис. 1.11 Графік функції розподілу релеевського закону

Визначимо числові характеристики випадкової величини з рівномірним розподілом.

Математичне очікування

Дисперсія

Середньоквадратичне відхилення

Коефіцієнт асиметрії

.

Ексцес дорівнює

Порядок виконання роботи

Кожен студент повинен виконати індивідуальне завдання відповідно до варіанту і зробити висновки на основі проведених теоретичних та практичних досліджень. У висновках потрібно вказати яких навичок та знань набули під час виконання індивідуального завдання .

В середовищі MathCad потрібно змоделювати закони розподілу випадкових величин відповідно до варіанту та дослідити числові характеристики (за допомогою вбудованих функцій MathCad та класичних формул).

Визначити головні характеристики випадкових величин:

• щільність розподілу ймовірностей;

• функція розподілу ймовірностей.

Визначити числові характеристики законів розподілу:

• математичне сподівання (перший центральний момент);

• дисперсію (другий центральний момент);

• середньоквадратичне відхилення;

• третій центральний момент (характеристика асиметрії розподілу);

• четвертий центральний момент (характеристика «крутизни» розподілу).

Порядок вибору варіанта:

Номер варіанту завдання відповідає порядковому номеру студента в журналі (табл.1).

Таблиця 1

Варіанти виконання лабораторної роботи №1

№ п/п	Одновимірні закони розподіли випадкових величин
	Експоненційний закон	Релеевський закон
	1	20
	2	30
	3	40
	4	50
	5	60
	7	70
	8	80
	9	1
	10	2
	11	3
	12	4
	13	5
	14	6
	15	7
	16	8
	17	9
	18	10
	19	10
	20	11
	30	12
	40	13
	50	14
	60	15
	70	16
	80	17
	1	18
	2	19
	3	20
	4	1
	5	2