Оценивание статистических характеристик динамических систем методом Монте-Карло

Сущность метода статистических испытаний состоит в построении оценок статистических характеристик случайных процессов, которые допускают построение своих реализаций. Совокупность реализаций случайного процесса служит основой для построения оценки математического ожидания в момент времени :

,

где – -я реализация реализации случайного процесса в момент времени , – количество реализаций, по которым строится оценка,

и оценки корреляционной матричной функции между моментами времени и :

,

где справедливы все ранее введенные соотношения.

Отметим, что в этом соотношении на месте оценки предпочтительно использовать само математическое ожидание (в случае, если сведения о нем доступны).

Оценка ковариационной матрицы может быть определена, как частный случай при .

Точность оценок

Оценки математического ожидания

и дисперсии

случайной величины , построенные на основе обработки ограниченной выборки ее реализаций , , сами являются случайными величинами.

Очевидно, что чем больше размер выборки реализаций, тем точнее несмещенная оценка, тем ближе она к истинному значению оцениваемого параметра. Ниже приведены приближенные формулы, основывающиеся на предположении об их нормальном распределении¹. Симметричный относительно доверительный интервал для оценки , соответствующий доверительной вероятности , определяется величиной , для которой справедливо соотношение:

,

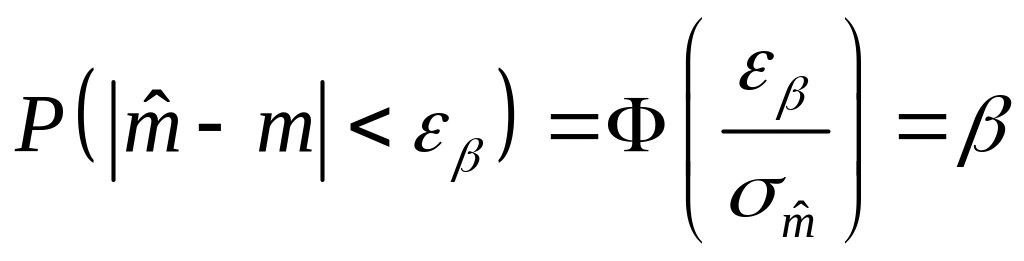где – истинное значение математического ожидания случайной величины , – среднеквадратическое отклонение случайной величины , 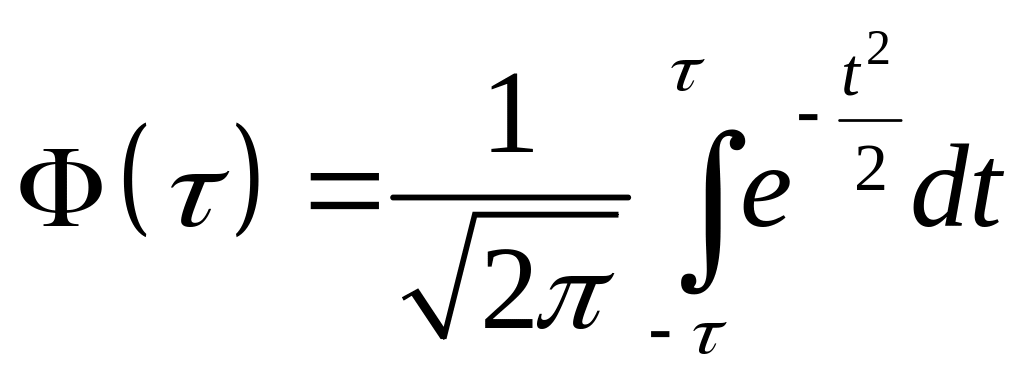– интеграл вероятностей.

На основе приведенного выше соотношения величина может быть определена следующим образом:

,

где – функция, обратная по отношению к интегралу вероятностей .

Поскольку характеристика рассеивания оценки нам в точности не известна, воспользуемся ее ориентировочным значением, вычисленным с использованием оценки :

.

Т.о. окончательное соотношение, связывающие точность оценки математического ожидания и размера выборки, по которой производится оценивание, выглядит следующим образом:

.

Это означает, что величина доверительного интервала (при неизменном значении доверительной вероятности ), расположенного симметрично относительно , выраженная в долях оценки среднеквадратического отклонения , обратно пропорциональна квадратному корню из размера выборки .

Доверительный интервал для оценки дисперсии определяется аналогичным образом:

с точностью до величины , которая за неимением более точной информации может быть приблизительно определена из соотношения:

.

Т.о. величина доверительного интервала (при неизменном значении доверительной вероятности ), расположенного симметрично относительно , выраженная в ее долях, обратно пропорциональна квадратному корню из величины , где – размер выборки.

Более точные формулы для построения доверительных интервалов¹ оценок могут быть получены с использованием точных сведений о законе распределения случайной величины .

Например, для гауссовского закона распределения случайная величина

подчиняется закону распределения Стъюдента с степенью свободы, а случайная величина

распределена по закону также с степенью свободы.