Прогноз

Для прогнозирования значения фазового вектора линейной системы

,

где – определяет неслучайное вынуждающее воздействие на систему; – определяет случайное воздействие на систему.

могут быть использованы соотношения прогноза, встречавшиеся выше при описании алгоритма калмановской фильтрации:

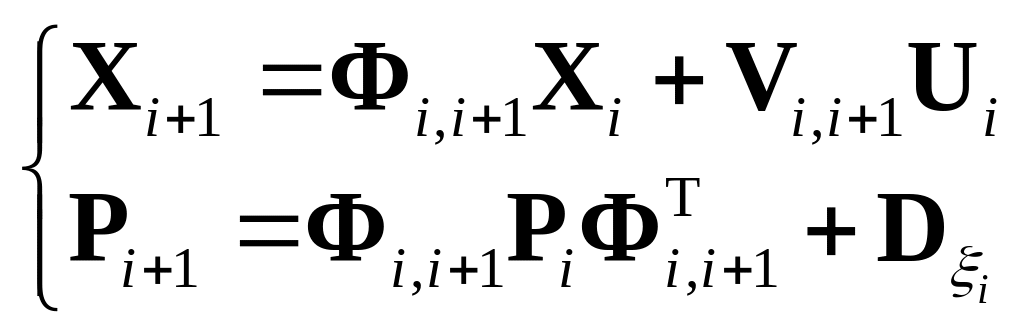
где – ковариационная матрица вектора .

Использование метода наименьших квадратов в нелинейных задачах

Как и Фильтр Калмана, метод наименьших квадратов может быть применен к линеаризованным моделям измерений. Пусть исходная нелинейная модель измерений имеет вид:

.

Тогда в результате линеаризации этой модели формально получим:

.

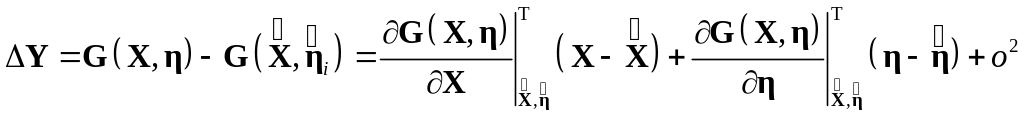Откуда, полагая и вводя обозначения:

; ; ,

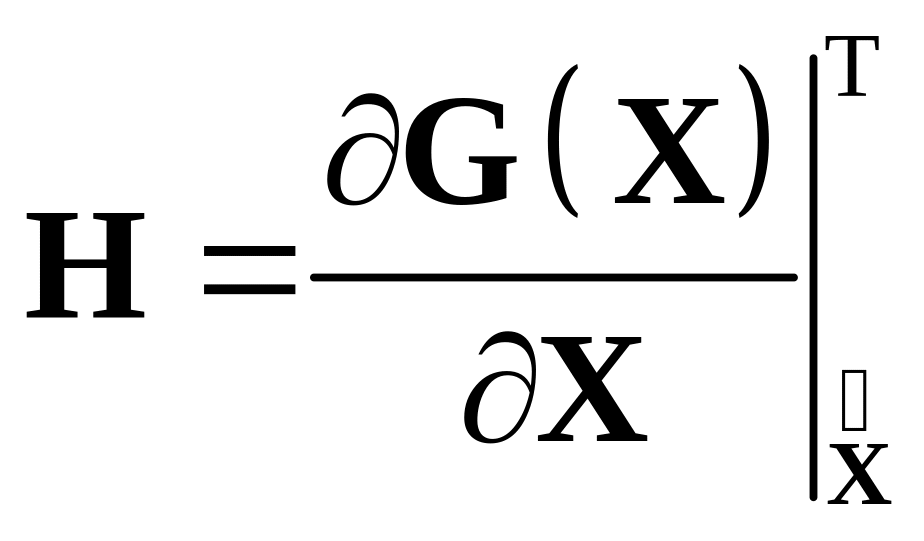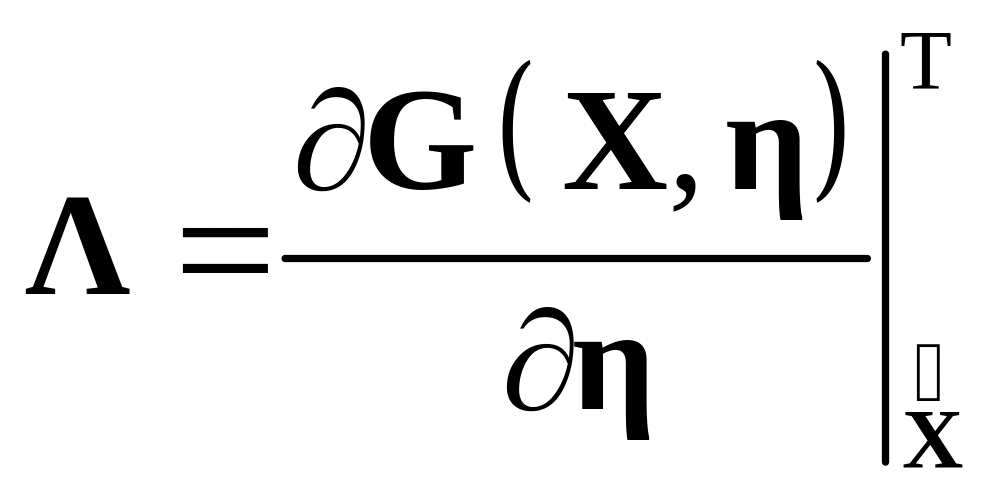получим результирующее соотношение:

.

Отсюда соотношение для построения оценки фазового вектора методом наименьших квадратов примет окончательный вид:

Построение матрицы Коши

В задачах построения оценок методами статистической обработки измерений часто встречается задача построения матрицы Коши. Эта матрица связывает фазовые векторы системы, отнесенные к разным моментам времени, в собственном движении.

Ограничимся в настоящем разделе рассмотрением вопросов, связанных с построением матрицы Коши для модели эволюции, записанной в виде системы обыкновенных дифференциальных уравнений (линейных или нелинейных).

Для линейной системы имеем:

.

Тогда дифференциальное уравнение для матрицы Коши примет вид:

.

Интегрируя его на интервале времени от до , с единичной матрицей соответствующей размерности в качестве начальных условий, получим матрицу Коши, связывающую фазовые векторы, отнесенные к моментам времени и :

.

В случае, когда модель эволюции фазового вектора представлена нелинейной системой дифференциальных уравнений общего вида:

,

матрица Коши может быть построена с использованием приведенных выше соотношений для линеаризованной системы:

,

где использованы следующие обозначения для матриц пропорциональности, построенных в окрестности опорной траектории , :

; .

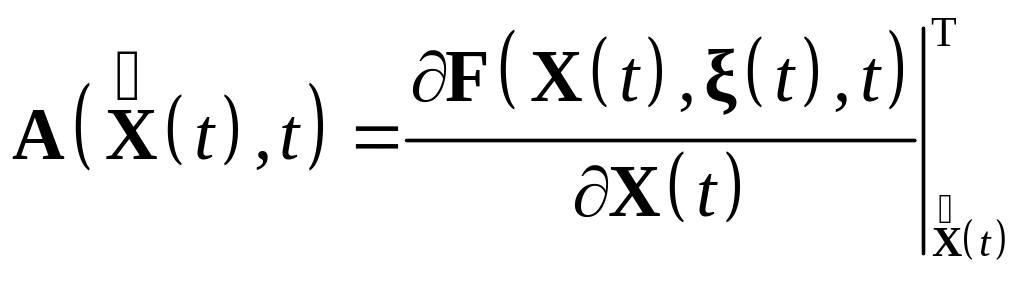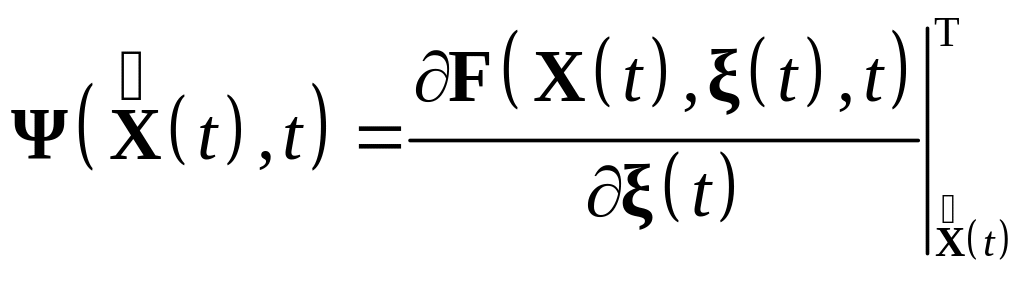Моделирование измерений

Проблема возникает в случае, когда, например, оценивая потенциально достижимую точность метода в некоторой задаче, Вы не располагаете какими-либо результатами измерениями. В этом случае результаты измерений требуется смоделировать. Особенность моделирования результатов измерений состоит в том, что модели движения и измерений, используемые для этой цели могут не совпадать с теми моделями, которые Вы будете использовать в ходе построения оценок с использованием того или иного метода фильтрации.

Более того, рекомендуется, чтобы модели, используемые для построения результатов измерений, были максимально точными, наилучшим образом приближенными к физическим процессам и закономерностям, наблюдающимся в природе.

В качестве начальных условий для моделирования эволюции фазового вектора динамической системы должны использоваться истинные значения координат этого вектора. Кроме этого места истинные значения координат фазового вектора системы не должны использоваться более нигде¹.

Численные методы

Специальные функции

Моделирование случайных величин

Моделирование случайных величин (случайных чисел) с требуемыми законом распределения вероятностей и значениями его используются, как правило, т.н. псевдослучайные числа. Псевдослучайные числа в основных чертах подобны соответствующим случайным величинам, однако, формируются они с использованием детерминированных алгоритмов, именуемых генераторами (псевдо-) случайных чисел.

Равномерно распределенные случайные величины

Как правило, все алгоритмы формирования случайных величин основываются на использовании равномерно распределенных на некотором интервале случайных чисел. Затем эти числа преобразуются таким образом, чтобы обеспечить соответствие полученной случайной величины требуемому закону ее распределения. Т.о. от вычислительных качеств алгоритма формирования равномерно распределенных случайных величин существенным образом зависят генераторы всех остальные случайных величин.

Поскольку целочисленная арифметика изучена лучше, чем арифметика рациональных чисел, для моделирования равномерно распределенной случайной величины используется следующее соотношение:

,

где и – целые числа; – некоторая функция, отображающая множество целых чисел на себя.

Очевидно, описанный выше вычислительный алгоритм необходимо инициализировать целым неотрицательным числом .

Известно немало видов функции , но здесь мы рассмотрим лишь широко применяемый на практике метод Коробова. Вычислительный алгоритм выглядит следующим образом:

,

где – большое простое число (например, 2027 или 5087); – целое число, отвечающее условию: , где – целое число ( ); – здесь оператор выделения целой части числа в скобках.

Генерируемое таким образом число с приблизительно равной вероятностью принимает значения на интервале от 1 до . При помощи нормировки и смещения получим произвольное равномерно распределенное рациональное число:

,

где и – соответственно, нижняя и верхняя границы интервала распределения генерируемой случайной величины.

Очевидно, что на любом интервале может быть сгенерировано счетное количество случайных величин (не более ). Т.о., самое большее, на -й итерации генерируемая последовательность повторится. Следовательно, для генерации равномерно распределенных случайных величин в соответствии с приведенным выше алгоритмом необходимо выбирать целочисленный тип данных, обладающий максимальной длинной, а в качестве – максимальное простое число, представимое в этом типе данных.

Как правило, современные средства разработки приложений располагают датчиком случайных, равномерно распределенных стандартных чисел . Моделирование случайных величин, равномерно распределенных на произвольном интервале, может быть выполнено на основе использования значений следующим образом:

.