Пособие для проведения практических занятий и методические указания к курсовому проектированию

Московский авиационный институт (Государственный технический университет) Кафедра 704

С. В. Кудряшов

Основы статистической динамики комплексных информационных систем

Пособие для проведения практических занятий и методические указания к курсовому проектированию

Москва, 2007

Оглавление

Оглавление 2

Введение 4

Априорный анализ динамических систем 5

Прохождение случайного сигнала через линейную систему 5

Эволюция фазового вектора системы 7

Эволюция ковариационной матрицы фазового вектора системы 8

Статистическая линеаризация 8

Первый способ 9

Второй способ 10

Вычисление коэффициентов линеаризации 10

Неоднозначность в нелинейных звеньях 13

Нелинейное звено, охваченное обратной связью 15

Моделирование случайных процессов 16

Формирующий фильтр 16

Моделирование белого шума 17

Оценивание статистических характеристик динамических систем методом Монте-Карло 18

Точность оценок 18

Нестационарные динамические системы 20

Стационарные динамические системы 21

Апостериорный анализ динамических систем 21

Фильтр Калмана 22

Модель движения 22

Модель измерений 22

Коррекция 23

Прогноз 23

Оценивание 23

Использование калмановской фильтрации в нелинейных задачах 25

Метод наименьших квадратов 27

Построение оценок 27

Прогноз 29

Использование метода наименьших квадратов в нелинейных задачах 29

Построение матрицы Коши 30

Моделирование измерений 30

Численные методы 31

Специальные функции 31

Моделирование случайных величин 31

^{Равномерно распределенные случайные величины 31}

^{Гауссовские случайные величины 32}

^{Случайные векторы 33}

Интеграл вероятностей 34

Полиномы Чебышева 35

Интегрирование обыкновенных дифференциальных уравнений 35

Методы Рунге-Кутты 36

^{Точность результатов численного интегрирования 36}

^{Вложенный метод Дормана-Принса 5(4) порядка 37}

Многошаговые методы 39

^{Методы Адамса 39}

Интегрирование уравнений с запаздывающим аргументом 40

Сравнение вычислительных качеств методов 40

^{Задача Аренсторфа 40}

^{Эллиптические функции Якоби 41}

^{Задача двух тел 41}

^{Уравнение Ван-дер-Поля 41}

^{«Брюсселятор» 42}

^{Уравнение Лагранжа для висячей струны 42}

^{«Плеяды» 42}

Оформление пояснительной записки 43

Титульный лист 43

Раздел «Оглавление» 43

Раздел «Введение» 44

Раздел «Теория» 44

Раздел «Алгоритм» 44

Раздел «Программа» 44

Раздел «Результаты» 44

Раздел «Выводы» 45

Раздел «Список использованных источников» 45

Приложения 45

Литература 46

Введение

В настоящем учебном пособии содержатся методические указания к выполнению заданий курсовых проектов и к проведению практических занятий по курсу «Основы статистической динамики».

Целью курсового проектирования и практических занятий является овладение студентами технологией априорного и апостериорного анализа нелинейных динамических систем, находящихся под воздействием случайных возмущений.

Априорный анализ динамических систем Прохождение случайного сигнала через линейную систему

К ак известно, статистические характеристики в установившемся режиме выходного случайного процесса (математическое ожидание и спектральная плотность ) линейной устойчивой динамической системы с передаточной функцией могут быть построены при известных характеристиках входного случайного стационарного процесса – и на основе использования следующих соотношений:

; ,

где:

– частотная характеристика линейной системы, получающаяся из путем формальной замены оператора Лапласа на (в предположении о равенстве нулю константы абсолютной сходимости ); – передаточная функция системы в установившемся режиме (при равенстве нулю всех производных) получается из путем формальной замены оператора Лапласа (или соответствующего ему в выражении передаточной функции системы оператора дифференцирования ) на 0; – квадрат модуля передаточной функции системы.

Используя полученную т.о. спектральную плотность выходного сигнала можно построить его корреляционную функцию , как результат обратного преобразования Фурье:

,

и дисперсию интегрированием спектральной плотности в бесконечных пределах по или приравнивая нулю аргумент корреляционной функции :

.

Р ассмотрим общий случай, когда на многомерную устойчивую систему воздействует стационарный векторный случайный процесс с известными статистическими характеристиками и , а выход системы определяется векторным случайным процессом со статистическим характеристиками, подлежащими определению. Каждый выход этой многомерной системы связан с каждым ее входом передаточной функцией . Передаточные функции образуют матричную передаточную функцию системы , так что:

.

Как известно, статистические характеристики выходного векторного случайного процесса имеют вид:

; .

Соответствующие спектральной плотности корреляционные функции могут быть получены посредством обратного преобразования Фурье, примененного к каждому компоненту матрицы :

.

Дисперсии компонент векторного случайного процесса могут быть построены при помощи интегрирования в бесконечных пределах по диагональных элементов матрицы или приравниванием нулю аргумента диагональных элементов его матричной корреляционной функции . Т.о. дисперсии компонент выходного случайного векторного процесса имеют вид:

.

Для общности изложения добавим, что входной векторный случайный процесс и выходной векторный процесс , полученный при прохождении через систему , корреляционно зависимы между собой. Они образуют единый случайный блочный вектор со соответствующей спектральной плотностью:

,

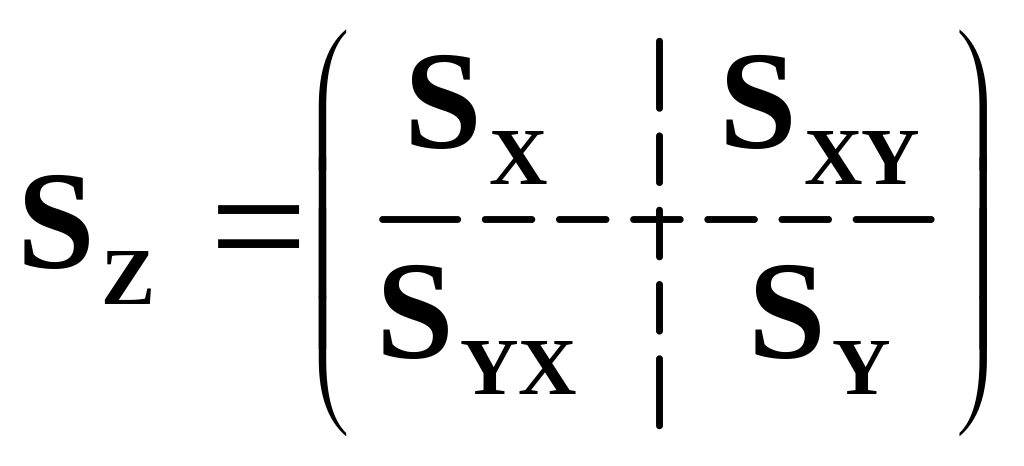где и – матрицы взаимных спектральных плотностей векторов и . Соответствующие и матричные корреляционные функции могут быть построены, как это было показано ранее, с использованием обратного преобразования Фурье.

При определении дисперсии случайного процесса путем интегрирования его спектральной плотности (с учетом четности ) приходится иметь дело с подынтегральными выражениями вида:

,

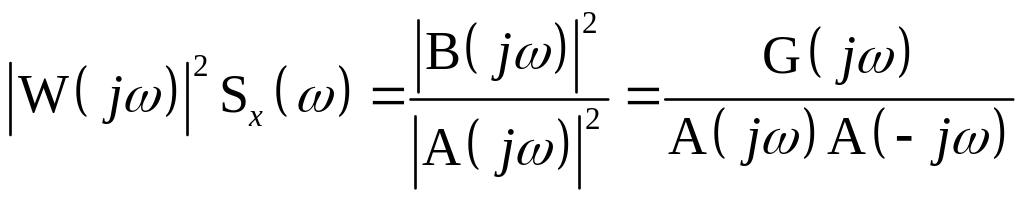где, с учетом того обстоятельства, что максимальная степень знаменателя составляет , а числителя в реальной системе – , полиномы и имеют вид:

; .

На основе предположения об устойчивости системы, все корни полинома лежат в верхней полуплоскости комплексной плоскости. Следовательно, интеграл может быть вычислен как сумма вычетов относительно этих самых корней полинома , как особых точек подынтегрального выражения, лежащих в верхней полуплоскости.

Результат суммирования вычетов может быть представлен в следующей компактной форме:

; ; ; ;

где

– зависит от значений коэффициентов полинома и совпадает (с точностью до знака) со старшим определителем Гурвица для системы, обладающей таким характеристическим полиномом; компоненты определителя обращаются в нуль в случае, если в полиноме отсутствует коэффициент индексом, требуемым правилами построения определителя; – получается путем замены множителя и компонент первой строки определителя на коэффициенты полинома .

При определении значений коэффициентов и следует обратить внимание на знак соответствующей степени .