6.3. Екситонне поглинання

Відповідно з викладеними вище міркуваннями, переходи електронів з валентної зони у зону провідності внаслідок поглинання світла можливі тільки тоді, коли енергія фотонів hν не менша ширині забороненої зони E_g. Проте експериментальні дослідження поглинання світла в області фундаментального поглинання закису міді (Cu₂O) показали, що кристал здатний поглинати кванти і з енергією, дещо меншою, ніж ширина забороненої зони, до того ж без появи електропровідності.

Пояснення цього явища полягає у припущенні можливості взаємодії збудженого світлом електрона з діркою, що утворилася у валентній зоні. В результаті цієї взаємодії електрон і дірка знаходяться у зв’язаному стані. При цьому вони здатні рухатись, обертаючись навколо спільного центра мас, який може поступально рухатися по кристалу. Віддаль між електроном і діркою (радіус екситона) становить декілька періодів ґратки кристалу. З цієї причини пара зв’язаних частинок (електрон і дірка) названа екситоном великого радіуса або екситоном Ваньє-Мотта.

У діелектриках і напівпровідниках з великою діелектричною проникністю основні особливості такого збудження описуються на основі найпростішої енергетичної моделі, де електрон і дірка розглядаються як квазічастинки з однаковими по величині зарядами протилежного знаку, що взаємодіють між собою з силою кулонівської взаємодії. У найпростішому випадку параболічних зон з екстремумом в центрі зони Бріллюена залежність енергії електрона провідності та дірки з валентної зони від хвильового вектора можна подати у вигляді

, , (6.8)

а рівняння Шредінґера системи взаємодіючих частинок електрон-дірка –

, (6.9)

де E – енергія системи у стаціонарному стані .

Для подальшого розгляду зручніше перейти від координат , електрона і дірки до нових змінних:

- – радіус-вектор центра мас екситона при спільному (переносному) рухові електрона й дірки;

- – координати їх відносного руху. Оскільки вказані рухи можуть здійснюватись незалежно один від одного, то введенням двох нових хвильових функцій і , кожна з яких описує один з цих рухів, рівняння Шредінґера зводиться до пари незалежних рівнянь, що описують рух пари в цілому, та їх відносний рух. Дійсно, поклавши у (6.9) , запишемо його у вигляді системи

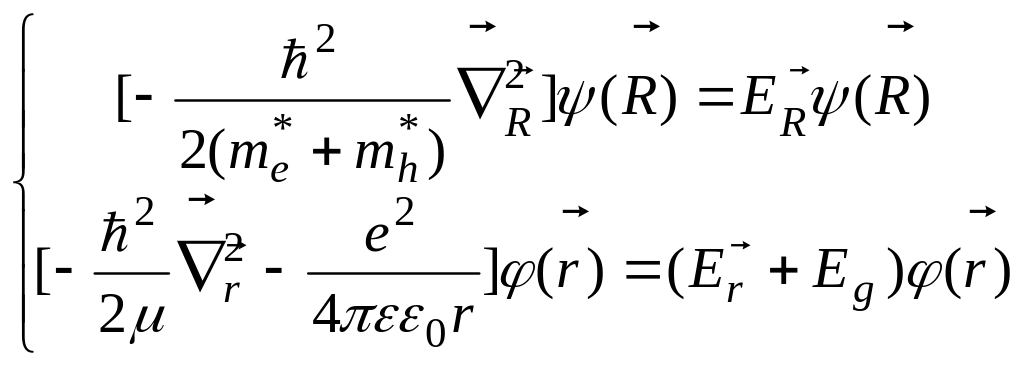
, (6.10)

де μ = m^*_em^*_h /(m^*_e + m^*_h) – приведена маса електрона і дірки, а E_R та E_r – енергії переносного та відносного рухів цієї пари частинок.

Розв'язком першого рівняння системи (6.10) є хвильова функція вільної частинки масою m_ex = m^*_e + m^*_h, що рухається у кристалі. Внаслідок трансляційної симетрії кристалу, вона повинна володіти хвильовими властивостями. Подібно до інших вільних частинок у кристалі – електрона провідності, дірки, – її функція стану може бути подана у вигляді плоскої хвилі

,

з хвильовим вектором . Енергія, яку переносить ця хвиля – енергія поступального руху екситона

. (6.11)

Друге рівняння системи (6.10) подібне до рівняння Шредінґера для електрона у атомі водню. Тому його розв’язок – енергію і функцію стану екситона, можна подати у вигляді, подібному до енергії і функції стану електрона у атомі водню, з умовою заміни маси електрона на приведену масу екситона μ та його заряду на величину e/ε. Тоді енергія зв’язаного стану екситона знаходиться за формулою, подібною до формули, що визначає енергію зв’язку електрона у атомі водню:

, (6.12)

а хвильова функція стану з енергією (6.11) може бути знайдена з відповідної хвильової функції електрона в атомі водню заміною його маси на ефективну масу електрона у кристалі, а постійної Рідберґа – на величину R_ex = μe⁴/ (2ћ²ε²) – постійна Рідберґа екситона (енергія зв'язку електрона і дірки в екситоні); n = 1, 2, … - квантове число. Зокрема, в основному стані екситона n = 1

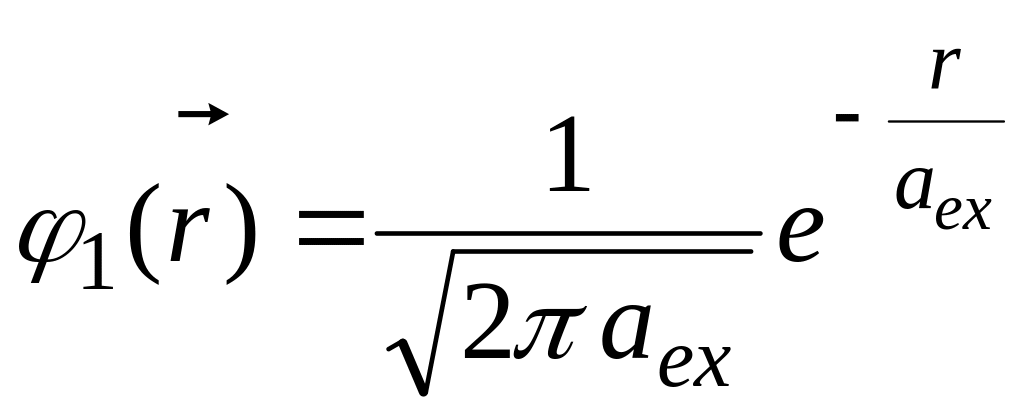, (6.13)

де – екситонний радіус Бора.

Повна енергія екситона є сумою (6.11) і (6.12); значення її при кожному значенні хвильового вектора квантуються, так що

, (6.14)

а нормована на об’єм кристалу Ω хвильова функція цього стану –

. (6.15)

При K = 0 перший доданок у (6.14) відсутній – є тільки відносний рух електрона і дірки, тоді як центр їх мас нерухомий. Це означає, що екситон Ваньє-Мотта можна уявити як пару „електрон-дірка”, що обертається навколо спільного центра мас. Другий доданок відповідає дискретним (n = 1, 2, 3, ...) збудженим станам водневоподібного атома з приведеною масою μ, який знаходиться в однорідному середовищі з діелектричною проникністю ε. Оскільки хвильовий вектор може набувати довільного з N значень у першій зоні Бріллюена (N – кількість атомів у кристалі), то кожному дискретному рівню n такого „атома” у кристалі відповідає енергетична зона певної ширини.

Окрім енергії, характеристикою екситонного стану є також радіус екситона – величина, що вводиться аналогічно до радіуса орбіти електрона у n-му стані атома водню:

. (6.16)

Відзначимо, що екситонні розміри можуть бути досить значними. Наприклад, у випадку класичного напівпровідника германію а_ех = 80а_В (а_В = 0,529 Å – борівський радіус атома водню), що значно перевищує розміри атома германію і постійну його ґратки а = 5,657 Å.

Оскільки енергія зв’язаного стану електрона менша, аніж у вільного (у межах зони провідності), то енергетичні рівні екситона, що визначаються формулою (6.12), знаходяться під дном зони провідності. Як показали експериментальні дослідження, глибина залягання їх у забороненій зоні становить близько 0,01 еВ. Переходи між цими рівнями супроводжуються поглинанням та випромінюванням енергії, що формує відповідний оптичний спектр. Очевидно, він має бути подібним до атомних спектрів – лінійчатим, з виконанням серіальних закономірностей. При цьому спектральні лінії екситонних серій зміщені відносно ліній водневоподібних атомів у бік ІЧ-діапазону, оскільки стала Рідберґа системи зв’язаних електрона й дірки R_еx значно менша її значення для атомів.

Збудження екситонів – перехід електронів з валентної зони екситонні стани, – супроводжується поглинанням світла. Саме цей процес називають екситонним поглинанням. Спостережуваний спектр екситонного поглинання має вигляд вузьких ізольованих смуг (а не ліній) на краю області фундаментального поглинання. Розширення спектральних ліній у смуги свідчить про можливість трансляційного руху екситона у кристалі.

Вперше експериментально екситонну спектральну серію було зареєстровано на краю смуги фундаментального поглинання кристалів закису міді, де було зареєстровано дві водневоподібні серії:

E_n = (2,173 - 0,0968/n²) eВ (n = 2, 3, 4, 5, 6),

та

E_n = (2,306 - 0,154/n²) eВ (n = 2, 3, 4).

Існування двох серій зумовлене екситонними станами, що утворюються двома валентними зонами та однією зоною провідності напівпровідника.

Водневоподібний спектр екситнів був спостережуваний експериментально також у інших кристалах. Зокрема, у кристалі дийодиду свинцю PbI₂ чотири інтенсивні лінії спектра екситонного поглинання описуються формулою

E_n = (2,568 - 0,142/n²) eВ (n = 2, 3, 4, 5).