Тема 14. Невизначений інтеграл та його властивості.
Поняття первісної.
Властивості первісних.
Невизначений інтеграл, його властивості.
Табличні інтеграли.
Геометрична інтерпретація невизначеного інтеграла.
Ф ункція, первісна, похідна, диференціал, інтегрування, невизначений інтеграл, таблиця інтегралів.
Функція F(x), визначена на проміжку (a,b), можливо нескінченому, називається первісною функції f(x) на цьому проміжку, якщо для кожного х з вказаного проміжку існує похідна F'(x) і виконується рівність F'(x) = f(x).
Операція знаходження первісної даної функції називається інтегруванням.
Властивості первісної
Якщо F(x) є первісною функції f(x) на проміжку Х, то довільну іншу первісну Ф(х) функції f(x) на Х можна подати у вигляді Ф(х) = F(x) + C, де С – довільна стала.
Множина
всіх первісних функції
f(x)
називається невизначеним інтегралом
і позначається
.
Термін інтеграл увів Якоб І Бернуллі у 1690 р., а його брат, Йоганн І Бернуллі, запропонував назву інтегральне числення. Цікаво, що в історії математики цей термін пов’язують з двома латинськими словами: integro — відновлювати (шукати початковий, «первісний» вигляд) та integer – цілий.
Властивості невизначеного інтеграла
Табличні інтеграли
1.
|
7.
|
2.
|
8.
|
3.
|
9.
|
4.
|
10.
|
5.
|
11.
|
6.
|
12.
|
Основна: . Додаткова: .
.
Що називають первісною даної функції?
Що означає термін «інтегрування»?
Сформулюйте основні властивості первісної.
Чим відрізняються поняття первісної та невизначеного інтеграла?
Чи однаковий результат дадуть диференціювання невизначеного інтеграла та знаходження диференціала від нього?
Чи можна виносити константу з-під знаку інтеграла??
Що означають з геометричної точки зору поняття «невизначений інтеграл» та «первісна»?
Тема 15. Основні методи інтегрування.
Метод безпосереднього інтегрування.
Метод заміни змінної.
Метод інтегрування частинами.
Інтегрування дробово-раціональних функцій.
Інтегрування ірраціональних виразів.
Інтегрування тригонометричних функцій.
П ервісна, змінна, похідна, диференціал, підінтегральна функція, підінтегральний вираз, раціональні дроби, ірраціональність.
Якщо підінтегральну функцію f(x) можна звичайними арифметичними перетвореннями привести до табличного вигляду, тоді інтегрування здійснюють безпосередньо, з використанням табличних інтегралів та властивостей невизначеного інтеграла.
З
найти
первісну для функції
.
.
У багатьох ситуаціях подібне перетворення підінтегральної функції можна виконати шляхом уведення іншої змінної. Такий спосіб називається методом заміни змінної.
Нехай функція х = φ(t) визначена і диференційовна на проміжку Т, а проміжок Х – множина її значень. Нехай також функція y = f(x) визначена на проміжку Х і має на ньому первісну F(х). Тоді на проміжку Т складена функція F(φ(t)) є первісною функції f(φ(t)).φ'(t), тобто виконується рівність
.
П
роінтегрувати
функцію
.
.
Іншим достатньо ефективним методом інтегрування є метод інтегрування частинами.
Нехай функції u(x) та v(x) визначені й диференційовні на проміжку Х, крім того, на цьому проміжку існує первісна функції u'(x).v(x). Тоді на проміжку Х існує первісна і функції u(x).v'(x), причому справедливий вираз
.
Проінтегрувати
функцію
.
Для визначення первісної використаємо метод інтегрування частинами:
Дробово-раціональними
називають функції, які можна представити
у вигляді
,
де P(x)
i Q(x)
– деякі многочлени степенів m
та n
відповідно.
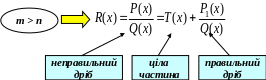
Будь-який правильний раціональний дріб розкладається на суму найпростіших раціональних дробів, коефіцієнти яких можна знайти методом невизначених коефіцієнтів.
В игляд вказаних найпростіших дробів визначається коренями знаменника.
В
изначити
інтеграл
.
Знаменник підінтегрального виразу можна розкласти на множники:
,
звідки: 
.
Зведемо праву частину рівності до спільного знаменника, що дозволить нам визначити невизначені коефіцієнти:
.
З
отриманої рівності визначаємо, що: а)
при х = 0
маємо
;
б) при х = 2
маємо
;
в) при х = –
4
маємо
.
Аналогічні значення коефіцієнтів можна отримати, прирівнявши в останній рівності коефіцієнти змінної х з однаковим показником степеня справа і зліва від знаку рівності. Отже, шуканий інтеграл буде дорівнювати:
=
=
.
В
изначити
інтеграл
.
Спробуємо розкласти знаменник на множники:
.
Отже, підінтегральну функцію можна зобразити так:
.
Звівши
дроби лівої частини рівності до спільного
знаменника та прирівнявши чисельники,
отримаємо значення коефіцієнтів:
а)
при х = -1
маємо
;
б)
при х = 0
маємо
;
в) при х = 1
маємо
.
При визначених коефіцієнтах розкладання набуде вигляду:
.
Інтегруючи таку рівність, отримаємо ряд табличних інтегралів, а, отже, і розв’язок:
.
В
изначити
інтеграл
.
Розкладемо підінтегральну функцію в ряд:
.
Повторюючи
попередні викладки, знайдемо значення
коефіцієнтів, і отримавши значення
,
і
,
підставимо їх у відповідні вирази. В
результаті матимемо:
.
Якщо підінтегральна функція містить ірраціональність і не належить до табличних форм, то перед проведенням інтегрування основним засобом є її «раціоналізація». Як правило, це відбувається шляхом підстановки замість ірраціональної складової деякої нової змінної, стосовно якої й проводять інтегрування. А після визначення інтеграла заміну проводять у зворотному порядку.
В
изначити
інтеграл
.
Усунемо
радикал з-під інтеграла, ввівши позначення
.
Тоді
,
а
.
Після таких перетворень досліджуваний
інтеграл набере вигляду:
.
Додамо і віднімемо від чисельника підінтегральної функції одиницю.
.
Обидва утворені інтеграли є табличними, що дозволяє записати відповідні первісні й повернутися до основної змінної:
.
При інтегруванні складних виразів з тригонометричними функціями звертають увагу на співвідношення між самими функціями та їх аргументами.
В
изначити
інтеграл
.
Застосуємо формулу перетворення добутку функцій в суму:
.
В
изначити
інтеграл
.
Застосуємо допоміжні формули перетворень і отримаємо:
.
В
изначити
інтеграл
.
Застосуємо запропоноване співвідношення між функціями:
.
В
изначити
інтеграл
.
Застосуємо наведену заміну змінної:
.
В
изначити
інтеграл
.
Оскільки
підінтегральна функція є непарною
відносно
,
скористаємося першою заміною
:
.
Основна: . Додаткова: .
Що означає термін «безпосереднє інтегрування»?
В чому полягає суть методу заміни змінної?
Яке правило використовують для доведення теореми про можливість заміни змінної?
В чому полягає основна мета методу інтегрування частинами?
Яку функцію називають дробово-раціональною?
Для чого застосовують метод невизначених коефіцієнтів?
Що є основним правило при інтегруванні ірраціональних виразів?
Опишіть правила інтегрування складних тригонометричних виразів.