Дифференциальные уравнения 2 порядка, допускающие понижение порядка
1
)
Уравнения вида:
уравнение решается двукратным интегрированием по переменной х.
Проинтегрируем 1 раз по х.
Проинтегрируем 2 раз по х
общее решение.
Замечание: для
дифференциального уравнения порядка
n:
-
интегрировать нужно n
раз.
Примеры:
2) Дифференциальные уравнения не содержащие явно y.
- нет явно y
Замена
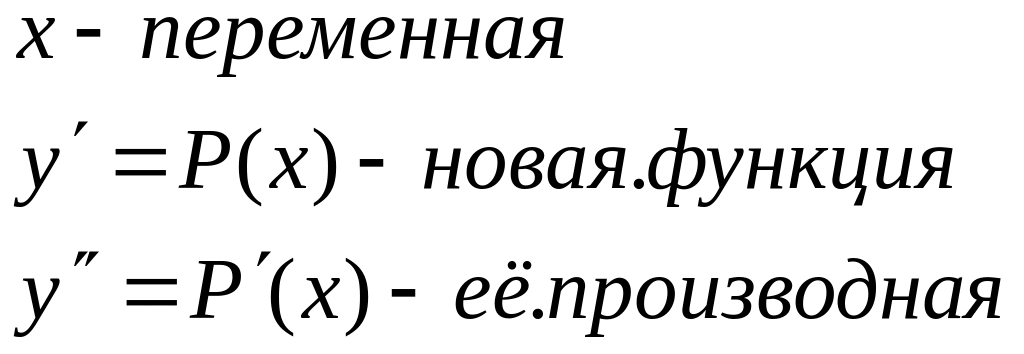
Подставим замену
в дифференциальное уравнение, получим
получим дифференциальное уравнение 1 порядка.
Найдём решение этого уравнения:
сделаем обратную
замену
п
роинтегрируем
обе части по х
-
общее решение
Пример:
3) Дифференциальные уравнения 2 порядка не содержащие явно х.
-
нет явно х.
З
амена:
у-новая переменная
-
новая функция
-
её производная
Подставим замену в исходное уравнение
получим дифференциальное уравнение 1 порядка:
-
его решение
Сделаем обратную
замену -
-
дифференциальное уравнение с разделяющимися
переменными. Разделим переменные:
;
-
общее решение (вид неявный)
Примеры:
1.
2.
Линейные дифференциальные уравнения высших порядков
Уравнение вида:
называется
линейным дифференциальным уравнением
высшего порядка, где a0,а1,…аn-функции
переменной х или константы, причём
a0,а1,…аn
и f(x)
считаются непрерывными.
Если a0=1(если
то
на него можно разделить)
уравнение примет вид:
Если
уравнение
неоднородное.
уравнение однородное.
Линейные однородные дифференциальные уравнения порядка n
Уравнение вида:
называются
линейными однородными дифференциальными
уравнениями порядка n.
Для этих уравнений справедливы следующие теоремы:
Теорема 1: Если
-
решение
, то сумма
-
тоже решение
Доказательство:
подставим сумму в
Т.к производная любого порядка от суммы равна суме производных, то можно перегруппироватся , раскрыв скобки:
т.к y1 и y2 – решение.
0=0(верно) сумма тоже решение.
теорема доказана.
Теорема 2: Если
y0-решение
,
то
- тоже решение
.
Доказательство: Подставим в уравнение
т.к С выносится за знак производной, то
т.к
решение,
0=0(верно)
Сy0-тоже
решение.
теорема доказана.
Следствие из Т1
и Т2: если
-
решения (*)
линейеая комбинация
-тоже
решение (*).
Линейно независимые и линейно зависимые системы функций. Определитель Вронского и его свойства
Определение:
Система функций
-
называется линейно независимой , если
линейная комбинация
коэффициенты
.
Определение:
Систему
функций
-
называют линейно зависимой, если
и
есть коэффициенты
.
В
озьмём
систему двух линейно зависимых функций
т.к
или
-
условие линейной независимости двух
функций.
Примеры:
1)
линейно независимы
2)
линейно зависимы
3)
линейно зависимы
Определение: Дана система функций - функций переменной х.
Определитель
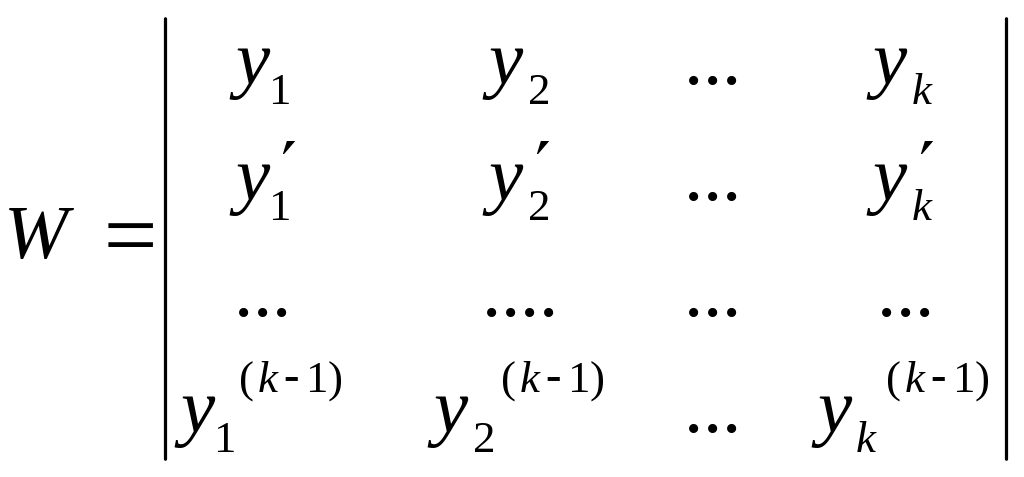-определитель
Вронского для системы функций
.
Для системы двух функций определитель Вронского выглядит следующим образом:
Свойства определителя Вронского:
Если - линейно зависимы на [a;b]
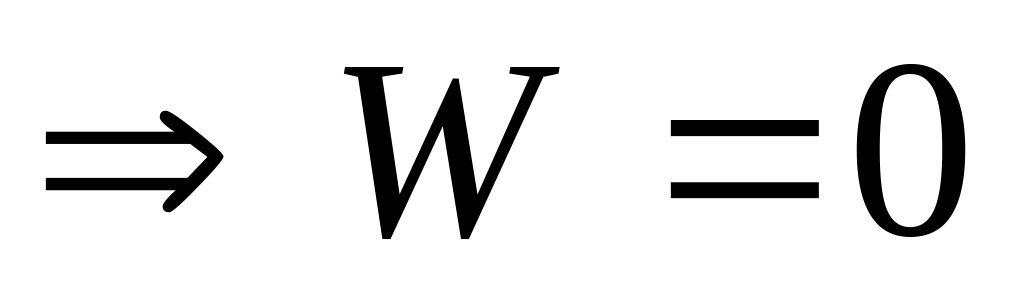на
этом отрезке.Если - линейно независимые, решения дифференциального уравнения
при
любых значениях х в области, где
определены функции а1…аn
Теорема: Об общем решении линейного однородного дифференциального уравнения 2 порядка.
Если y1 и y2 – линейно независимые решения линейного однородного дифференциального уравнения 2 порядка, то
общее
решение имеет вид:
Доказательство:
-
решение по следствию из Т1 и Т2.
Если даны начальные
условия то
и
должны находится однозначно.
-
начальные условия.
Составим систему для нахождения и . Для этого подставим начальные условия в общее решение.
определитель этой
системы:
-
определитель Вронского, вычисленный в
точке х0
т.к
и
линейно
независимы
(по
20)
т.к определитель
системы не равен 0, то система имеет
единственное решение и
и
находятся из системы однозначно.
