Порядок выполнения работы:
1 Составить модельную задачу и отладить на ней программу.
2 Решить задачу для конкретного варианта.
3 Вывести результаты решения модельной задачи для различного числа узлов N в виде:
4. Вывести результаты для поставленной задачи:
-
)
)
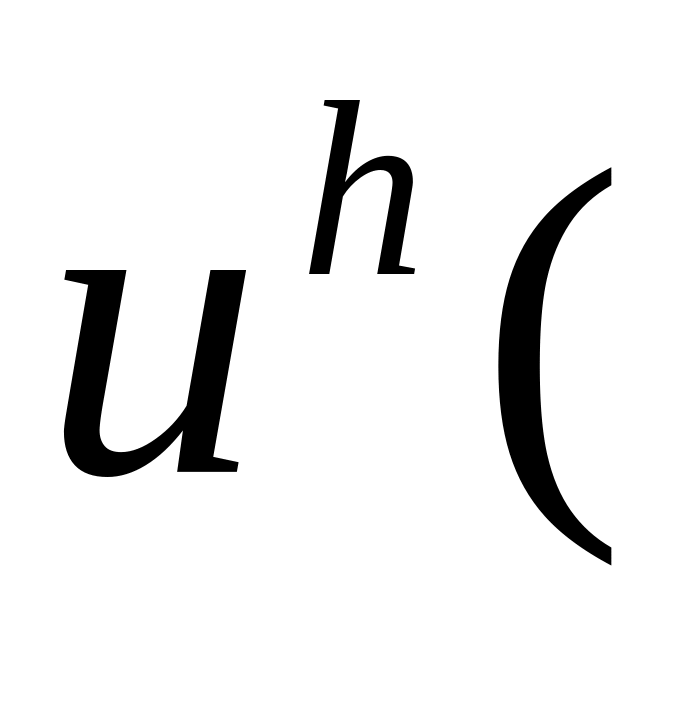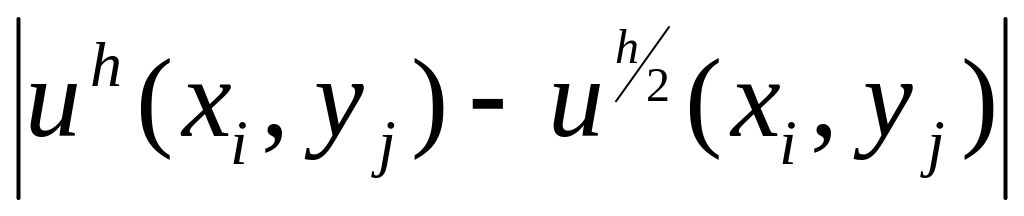
5 Внести случайную погрешность в начальные данные и, проведя вычисления для измененных данных, сделать вывод об устойчивости.
6. Проанализировать результаты.
Типовое задание к лабораторной работе
Решить эллиптическое уравнение
в D,
u=0 на ,
Варианты заданий
1 
2 
3 
4 
5 
6 
7 
8 
9 
10 
11 
12 
13 
14 
15 
16 
17 
18 
19 
20 
21 
22 
23 
24 
25 
Лабораторная работа №5
Приближенное решение уравнения Фредгольма
Цель работы: решить уравнение Фредгольма 2-го рода интерполяционным методом квадратур.
Теоретическая часть
Рассмотрим интегральное уравнение Фредгольма 2-го рода
.
(5.1)
Метод основан на интерполировании неизвестной функции . Для определенности изложения будем иметь в виду алгебраическое интерполирование.
Выберем
на отрезке [a,
b]
n
различных
точек
и
выполним интерполирование функции
по ее значениям в этих точках. Воспользуемся
лагранжевым
представлением интерполяционного
многочлена
(5.2)
где
.
Внесем это представление в интегральный член уравнения (5.1):
(5.3)
(5.4)
Чтобы
получить систему уравнений для
(хп),
отбросим
в (5.3) остаточный член
и в полученном приближенном
равенстве положим х
равным
:
(5.5)
После решения
системы (5.5) мы будем знать приближенные
значения
;
решения
в точках
.
Чтобы
найти приближенные значения
всюду на [а,b],
можно
выполнить алгебраическое интерполирование
по
значениям
.
Замечание. Интегралы (5.4) следует вычислять по квадратурным формулам Ньютона-Котеса.
Порядок выполнения работы:
1 Составить модельную задачу и отладить на ней программу.
2 Решить задачу для конкретного варианта.
3 Вывести результаты решения модельной задачи и для конкретного варианта для различного числа узлов.
4 Внести случайную погрешность в начальные данные и, проведя вычисления для измененных данных, сделать вывод об устойчивости.
5. Проанализировать результаты.
Типовое задание к лабораторной работе
Решить уравнение Фредгольма
Варианты заданий
1 
2 
3 
4 
5 
6 
7 
8 
9 
10 
11 
12 
13 
14 
15 
16 
17 
18 
19 
20 
21 
22 
23 
24 
25 
Лабораторная работа №6
Приближенное решение уравнений типа потенциала
Цель работы: найти приближенное решение гиперсингулярного интегрального уравнения.
Теоретическая часть
К гиперсингулярным уравнениям приводят многие задачи математической физики, например, это задача дифракции акустической волны на тонком, бесконечно протяженном, «жестком» экране.
Рассмотрим гиперсингулярное уравнение
(6.1)
Операцию дифференцирования нельзя внести под знак интеграла, так как получится расходящийся несобственный интеграл. Поэтому уравнение (6.1) является интегродифференциальным.
Приближенное решение уравнения (6.1) будем искать в виде разложения по многочленам Чебышева 2-го рода:
, (6.2)
где
Правую часть также разложим по многочленам Чебышева 2-го рода
, (6.3)
где
коэффициенты
определяются по формулам
Подставим эти выражения в уравнение (6.1). Воспользуемся формулами
(6.4)
(6.5)
получим
(6.6)
Отсюда
находим, приравнивая коэффициенты при
в левой и правой частях формулы (6.6),
. (6.7)
В результате имеем единственное приближенное решение
. (6.8)