Зв'язок ознак, виміряних в інтервальних шкалах

Якщо ознаки Х та Y виміряні у інтервальних шкалах, то для перевірки залежності між ними потрібно оцінити коефіцієнт лінійної кореляції між цими ознаками. Відмінність від нуля коефіцієнта лінійної кореляції свідчитиме про наявність зв’язку між досліджуваними ознаками.

Оцінкою коефіцієнта лінійної кореляції за вибіркою служить вибірковий парний коефіцієнт кореляції Пірсона

,

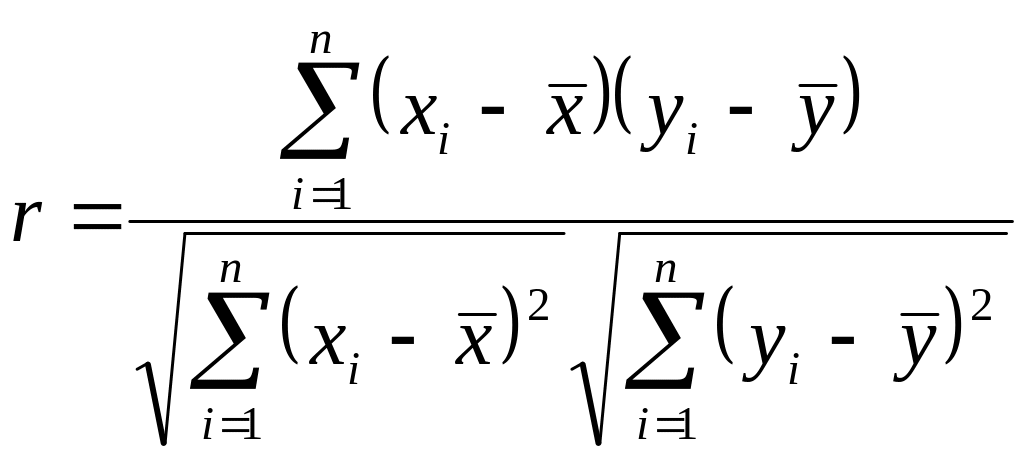де п — кількість спостережень, — вибіркові середні вибірок та відповідно.

Якщо ознаки Х та Y розподілені нормально, то величина r не тільки дає відповідь на питання про залежність досліджуваних ознак, але й вимірює тісноту їх зв’язку. Тому в цьому випадку доводиться поряд з гіпотезою часто доводиться перевіряти гіпотезу . Статистика

,

яку називають перетворенням Фішера від r, дозволяє робити ці перевірки незалежно від величини r, оскільки її розподіл апроксимується нормальним розподілом з дисперсією , залежною лише від об’єму вибірки.

Таким чином, якщо , де — квантиль рівня розподілу Стьюдента з ступенем вільності, то на рівні значущості гіпотезу про незалежність ознак відхиляємо і приймаємо альтернативну гіпотезу. Два коефіцієнти парних кореляцій і за вибіркою об’ємом вважатимемо статистично відмінними на рівні значущості , якщо їх перетворення Фішера задовольняють нерівність .

У пакеті Statistica 6.0 реалізовано у субмодулі Сorrelation matrices модуля Basic Statistics/Tables.

Приклад 41¹. Кожному з 17 досліджуваних по черзі пропонувались світловий і звуковий сигнали. Інтенсивність сигналів не змінювалась протягом всього експерименту. Час (у мілісекундах) між сигналом і реакцією досліджуваного наведено в таблиці. Чи можна стверджувати, що час реакції на звук і на світло незалежні.

№ досл.	1	2	3	4	5	6	7	8	9	10	11	12	13	14	15	16	17
Звук	223	104	209	183	180	168	215	172	200	191	197	183	174	176	155	115	163
Світло	181	191	173	151	168	176	163	152	155	156	178	160	164	169	155	122	144

Розв’язання: Сформулюємо статистичні гіпотези.

Н₀: Ознаки незалежні одна з одною.

Н₁: Ознаки пов’язані між собою.

В несемо дані в пакет Statistica 6.0. В модулі Basic Statistics/Tables виберемо субмодуль Сorrelation matrices. У першому списку змінних вказуємо обидві змінні. На закладці Options вибираємо варіант Display r, p-levels and N’s, що дасть змогу обчислити не тільки матрицю парних кореляцій, але й рівень значущості кожного з коефіцієнтів, та натискаємо кнопку Summary. Результат обчислень показано на рис. 32.

Як бачимо парний коефіцієнт кореляції дорівнює 0,242 і не є статистично значимим. Тому приймаємо нульову гіпотезу: час реакції на звук і світло не залежать один від одного.