
- •Уровень 1
- •Уровень 2
- •Дифференциальные уравнения
- •Алгебра и теория чисел
- •Темы практических заданий Литература
- •Линейная алгебра
- •Темы практических заданий Литература
- •Аналитическая геометрия (Небукина г.Ф.)
- •Темы практических заданий Литература
- •Топология
- •Темы практических заданий Литература
- •Дифференциальная геометрия
- •Темы практических заданий Литература
- •2009 (Жукова н.И.)
- •Функциональный анализ
- •Темы практических заданий Литература
- •Теория функций комплексного переменного
- •Уравнения с частными производными (Калинин а.В.)
- •Темы практических заданий
- •Литература
- •Вариационное исчисление и методы оптимизации (Сумин м.И.)
- •Темы практических заданий
- •Литература
Линейная алгебра
Векторное пространство. Базис, размерность. Подпространства и операции над ними. Замена базиса и пересчет координат. Линейные отображения векторных пространств и их матрицы. Собственные числа и собственные вектора линейного оператора. Квадратичные формы и их матрицы. Приведение квадратичной формы к каноническому виду. Закон инерции. Евклидово пространство. Неравенство Коши-Буняковского. Процесс ортогонализации. Самосопряженные операторы. Канонический вид матрицы самосопряженного оператора. Приведение квадратичной формы к главным осям. Пары форм. Жорданова матрица. Приведение числовой матрицы к жордановой форме. Ортогональные операторы и их свойства. Канонический вид матрицы ортогонального оператора.
Темы практических заданий Литература
Вопросы по теории (Баландин А.В.)
Собственные значения и собственные векторы линейного оператора.
Теорема о размерности суммы и пересечения подпространств.
Теорема о размерности ядра и образа линейного оператора.
Ортогональные операторы и их свойства.
Задачи
Уровень 1
Найти собственные векторы линейного оператора, заданного матрицей
 .
.Найти жорданову форму матрицы
 .
.Привести квадратичную форму
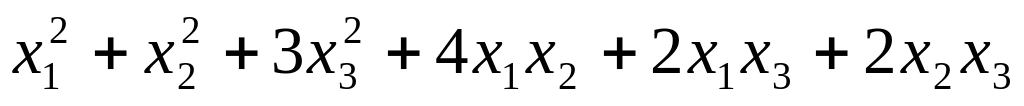 к каноническому виду методом Лагранжа.
к каноническому виду методом Лагранжа.Найти матрицу линейного оператора
 ,
если
,
если
 .
.Проверить является ли сумма
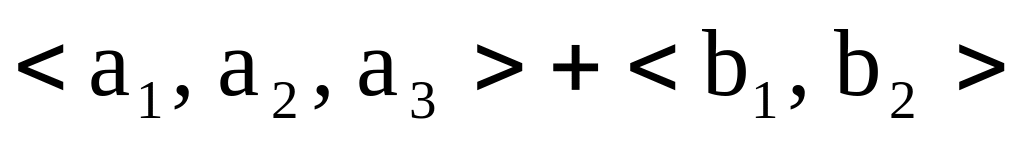 прямой, если
прямой, если
 ,
,
 ,
,
 ,
,
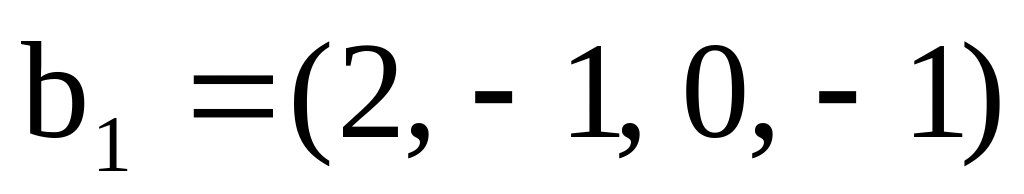 ,
,
 .
.Привести к главным осям квадратичную форму
 ,
не находя самого преобразования.
,
не находя самого преобразования.Ортогонализировать систему векторов
 .
.Задать системой линейных уравнений линейную оболочку системы векторов
 ,
,
 .
.Найти ортогональную проекцию вектора
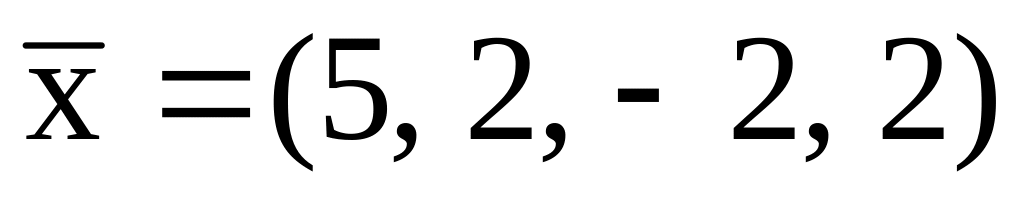 на подпространство
на подпространство
![]()
Найти ортонормированный базис из собственных векторов для линейного преобразования, заданного в ортонормированном базисе матрицей
 .
.Систему векторов
 арифметического пространства со
стандартным скалярным произведением
доролнить до ортонормированного базиса.
арифметического пространства со
стандартным скалярным произведением
доролнить до ортонормированного базиса.
Уровень 2
Найти базис в сумме и пересечении подпространств
 и
и
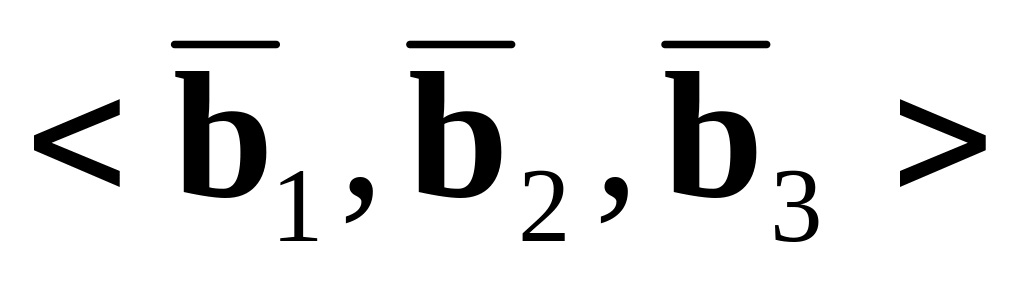 ,
если
,
если
 ,
,
 .
.Привести квадратичную форму
 к главным осям, т.е. найти ортогональное
преобразование, приводящее квадратичную
форму к каноническому виду.
к главным осям, т.е. найти ортогональное
преобразование, приводящее квадратичную
форму к каноническому виду.Найти минимальный многочлен матрицы
 .
.Найти жорданову форму матрицы
 .
.Выяснить, подобны ли матрицы
 и
и
 .
.(ЛУЧШЕ НЕ ДАВАТЬ) Найти базис двумерного подпространства, инвариантного относительно ортогонального оператора, заданного в ортонормированном базисе матрицей
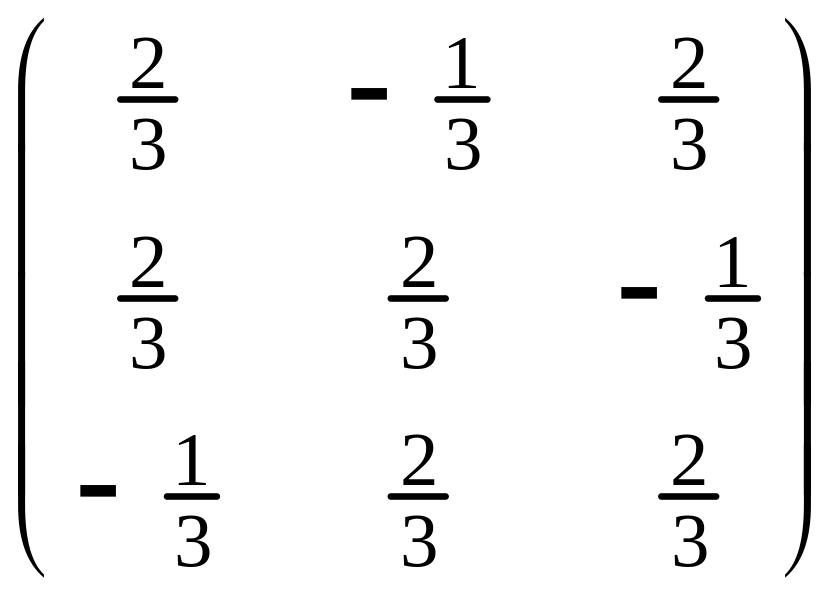
Найти ортогональную проекцию вектора
 на подпространство
на подпространство
![]()
Пусть
 – ортонормированный базис и линейный
оператор
– ортонормированный базис и линейный
оператор
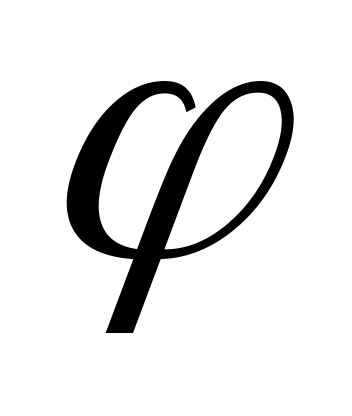 в базисе
в базисе
 имеет матрицу
имеет матрицу
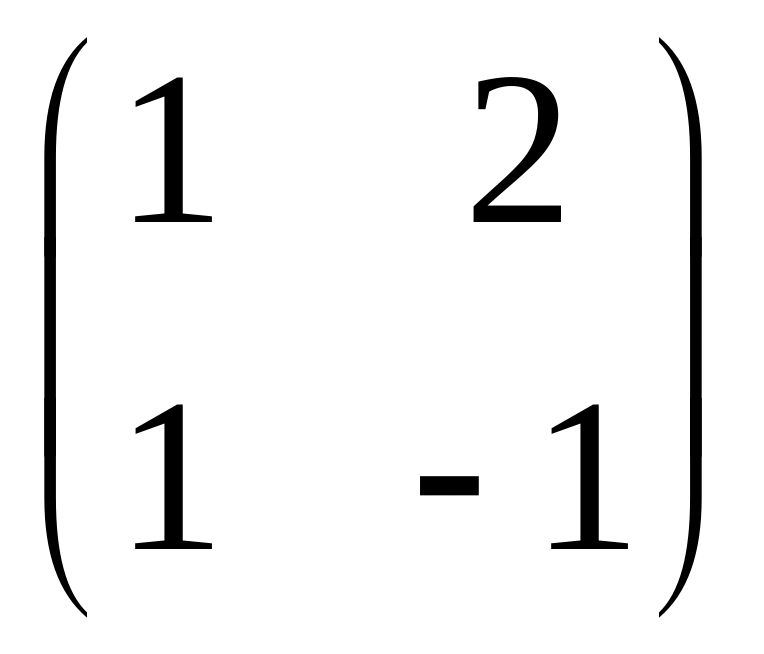 .
Найти матрицу сопряженного оператора
в базисе
.
.
Найти матрицу сопряженного оператора
в базисе
.Найти базис образа и ядра линейного оператора, заданного в некотором базисе матрицей
 .
.Не находя линейного преобразования, найти канонический вид следующей пары квадратичных форм:
![]() .
.
Найти ортонормированный базис в ортогональном дополнении к подпространству
![]()
Аналитическая геометрия (Небукина г.Ф.)
Свободные векторы, линейные операции над ними. Линейная зависимость векторов, геометрический смысл. Базис, координаты вектора в данном базисе. Скалярное, векторное и смешанное произведения векторов.
Аффинная и прямоугольная системы координат, преобразования: параллельный перенос и поворот осей координат.
Прямая линия на плоскости, различные виды ее уравнений. Пучок прямых на плоскости. Плоскость, различные виды ее уравнений. Взаимное расположение двух плоскостей. Пучок плоскостей и связка плоскостей. Прямая линия в пространстве, ее уравнения. Взаимное расположение двух прямых в пространстве. Взаимное расположение прямой и плоскости.
Кривые второго порядка, канонические уравнения. Директориальное свойство эллипса и гиперболы. Касательные к кривым второго порядка, оптические свойства. Кривые второго порядка как конические сечения. Приведение общего уравнения кривой второго порядка к каноническому виду. Поверхности второго порядка, канонические уравнения. Поверхности вращения. Прямолинейные образующие поверхностей второго порядка.
Аффинные преобразования плоскости, примеры. Группа аффинных преобразований, инварианты. Теорема об аффинной классификации кривых второго порядка.
