
- •Уровень 1
- •Уровень 2
- •Дифференциальные уравнения
- •Алгебра и теория чисел
- •Темы практических заданий Литература
- •Линейная алгебра
- •Темы практических заданий Литература
- •Аналитическая геометрия (Небукина г.Ф.)
- •Темы практических заданий Литература
- •Топология
- •Темы практических заданий Литература
- •Дифференциальная геометрия
- •Темы практических заданий Литература
- •2009 (Жукова н.И.)
- •Функциональный анализ
- •Темы практических заданий Литература
- •Теория функций комплексного переменного
- •Уравнения с частными производными (Калинин а.В.)
- •Темы практических заданий
- •Литература
- •Вариационное исчисление и методы оптимизации (Сумин м.И.)
- •Темы практических заданий
- •Литература
ПРОГРАММА
государственного междисциплинарного экзамена по специальности
010101.65 «Математика»
2009
от
МАТЕМАТИЧЕСКИЙ АНАЛИЗ
Функция. Предел последовательности и функции. Критерий Коши для числовых последовательностей. Предельные точки множеств. Теорема Больцано - Вейерштрасса. Непрерывные функции. Свойства функций, непрерывных в точке. Равномерная непрерывность функций. Теоремы Вейерштрасса, Кантора.
Дифференциалы и производные. Производные и дифференциалы высших порядков. Основные теоремы дифференциального исчисления: Ролля, Лагранжа, Коши. Формула Тейлора. Остаточный член в форме Пеано, Лагранжа, Коши. Приложения дифференциального исчисления к исследованию функций одной переменной.
Функции многих переменных. Функции многих переменных, пределы, непрерывность, частичные пределы. Свойства непрерывных функций. Частные производные. Дифференцируемость функции многих переменных. Дифференциал функции и его геометрический смысл. Производная по направлению и градиент. Производные и дифференциалы высших порядков. Формула Тейлора. Экстремум. Отображения Rn в Rm . Матрица Якоби теоремы о неявных функциях. зависимость функций. локальное обращение дифференцируемого отображения Rn в Rm . Условный экстремум. Замена переменных.
Неопределенный интеграл. Первообразная функция. Неопределенный интеграл и его основные свойства. Правила и методы интегрирования.
Определенный интеграл Римана. Условия интегрируемости. Классы интегрируемых функций. Основные свойства интеграла. Существование первообразной для непрерывной функции. Формула Ньютона-Лейбница. Длина дуги, площадь, объем тела вращения.
Несобственные интегралы. Интегралы с бесконечными пределами и интегралы от неограниченных функций. Абсолютная и условная сходимость. Признаки абсолютной и условной сходимости.
Ряды. Сходимость и сумма ряда. Абсолютная и условная сходимость. Знакопостоянные числовые ряды. Признаки сравнения. Интегральный признак Коши. Обобщенный гармонический ряд. Теорема Лейбница о сходимости знакочередующегося ряда.
Функциональные последовательности и ряды. Равномерная сходимость функциональных последовательностей и рядов. Критерий равномерной сходимости. Признак Вейерштрасса равномерной сходимости функционального ряда. Степенной ряд в комплексной области. 1-я теорема Абеля. Круг сходимости. Формула Коши-Адамара. Непрерывность суммы степенного ряда. Дифференцирование и интегрирование степенного ряда. Представление функций в виде ряда Тейлора. Необходимые и достаточные условия разложения функции в ряд Тейлора. Разложение в ряд Маклорена-Тейлора тригонометрических, показательной, логарифмической функции. Биномиальный ряд. Собственные интегралы, зависящие от параметра. Предельный переход под знаком собственного интеграла, зависящего от параметра. Непрерывность, дифференцирование и интегрирование по параметру. Несобственные интегралы, зависящие от параметра. Равномерная сходимость. Признак равномерной сходимости Вейерштрасса. Предельный переход под знаком несобственного интеграла, зависящего от параметра. Непрерывность, дифференцирование и интегрирование по параметру.
Pяды Фурье. Ортогональные системы функций. Коэффициенты Фурье по ортогональной системе. Ряд Фурье по тригонометрической системе периода 2l. Комплексная запись ряда Фурье. Неравенство Бесселя. Порядок стремления к нулю коэффициентов ряда Фурье. Теоремы о сходимости рядов Фурье. Интегрирование и дифференцирование рядов Фурье. Понятие полноты и замкнутости ортогональных систем. Критерий полноты - равенство Парсеваля. Полнота основной тригонометрической системы. Кратные интегралы. Двойные и тройные интегралы. Сведение двойных и тройных интегралов к повторным. Замена переменных в двойных и тройных интегралах.
Криволинейные интегралы и формула Грина. Криволинейные интегралы первого и второго рода, их выражение через определенный интеграл. Формула Грина о связи между двойным и криволинейным интегралом. Условие независимости криволинейного интеграла от пути. Интегрирование полных дифференциалов. Нахождение функции по ее полному дифференциалу.
Поверхностные интегралы. Определение стороны поверхности с помощью непрерывного поля нормалей. Двусторонние и односторонние поверхности. Ориентация поверхности и связь со стороной поверхности. Определение площади поверхности.
Темы практических заданий
Литература
Вопросы по теории (Ерахтина Г.М.)
Теорема Больцано-Вейерштрасса для числовых последовательностей и числовых множеств.
Непрерывность функции одной переменной в точке и на множестве. Теорема Вейерштрасса об ограниченности функции, непрерывной на замкнутом ограниченном множестве.
Понятие производной и ее геометрический смысл. Уравнения касательной и нормали к графику функции одной переменной.
Теорема о представлении функции одной переменной по формуле Тейлора с остатком в форме Пеано.
Понятие интеграла Римана. Интегрируемость функции, непрерывной на отрезке.
Понятие первообразной и неопределенного интеграла. Теорема о существовании первообразной для функции, непрерывной на интервале.
Понятие дифференцируемости функции многих переменных. Необходимые и достаточные условия дифференцируемости.
Понятие экстремума функции двух переменных. Необходимые и достаточные условия локального максимума (или минимума по выбору).
Понятие неявной функции одной переменной. Теорема о существовании однозначной непрерывной неявной функции одной переменной.
Признак сравнения в предельной форме для положительных числовых рядов.
Понятие равномерной сходимости функционального ряда. Теорема о непрерывности суммы равномерно сходящегося функционального ряда.
Определения несобственных интегралов по бесконечному промежутку и от неограниченной функции. Признак сравнения для несобственных интегралов по бесконечному промежутку от положительных функций.
Понятие равномерной сходимости для несобственного интеграла, зависящего от параметра. Теорема о непрерывности несобственного интеграла по параметру.
Формула Грина, связывающая криволинейный интеграл 2 рода по замкнутому контуру с двойным интегралом по соответствующей области. Вывод формулы Грина.
Условия независимости криволинейного интеграла 2-го рода от пути интегрирования.
Теорема о сходимости тригонометрического ряда Фурье кусочно-гладкой функции одной переменной.
Задачи
Вариант 1
Уровень 1
Для функции
 ,
заданной неявно уравнением
,
заданной неявно уравнением
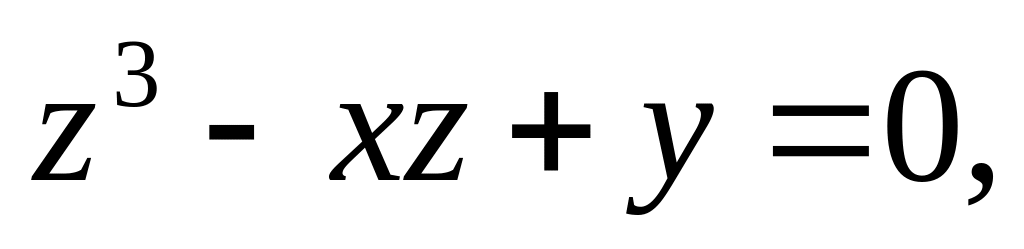 найти
найти
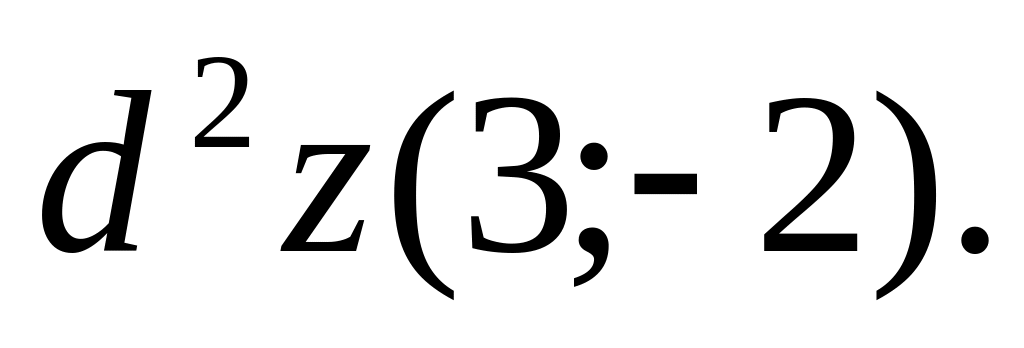
Преобразовать к новым независимым переменным
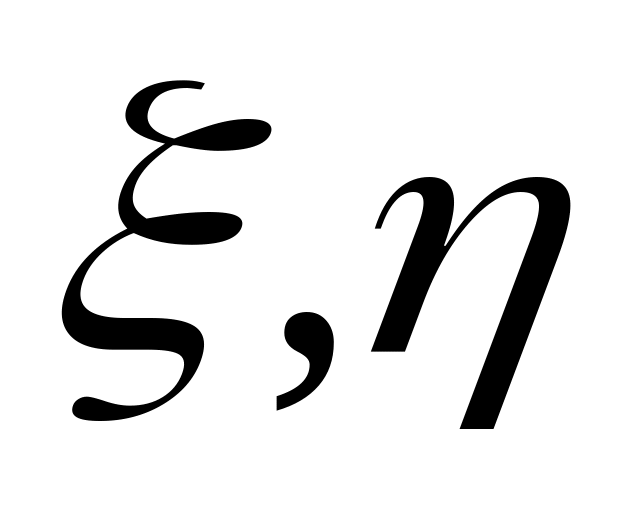 производную
производную
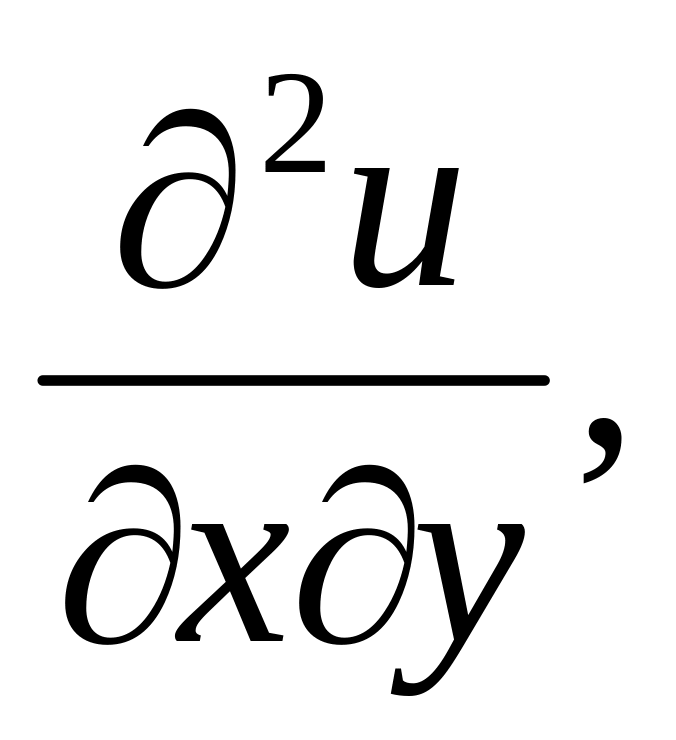 полагая
полагая
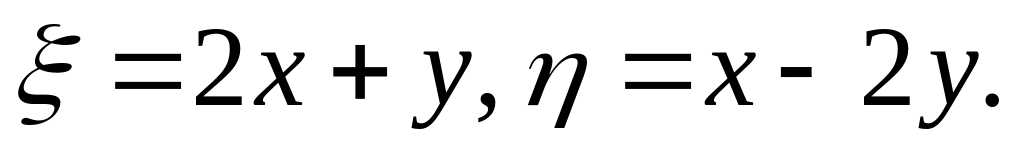
Исследовать на сходимость
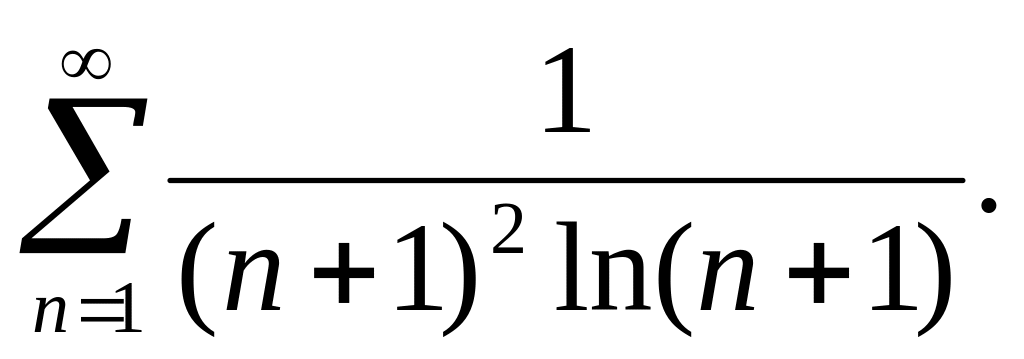
Исследовать на сходимость

Найти область сходимости ряда

Разложить в ряд Маклорена
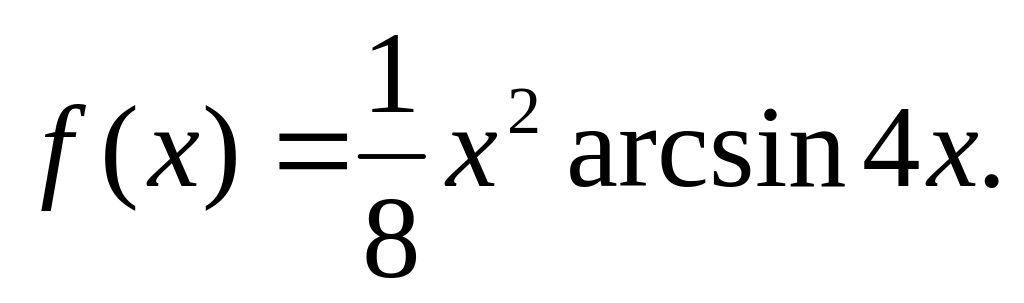
Исследовать на сходимость
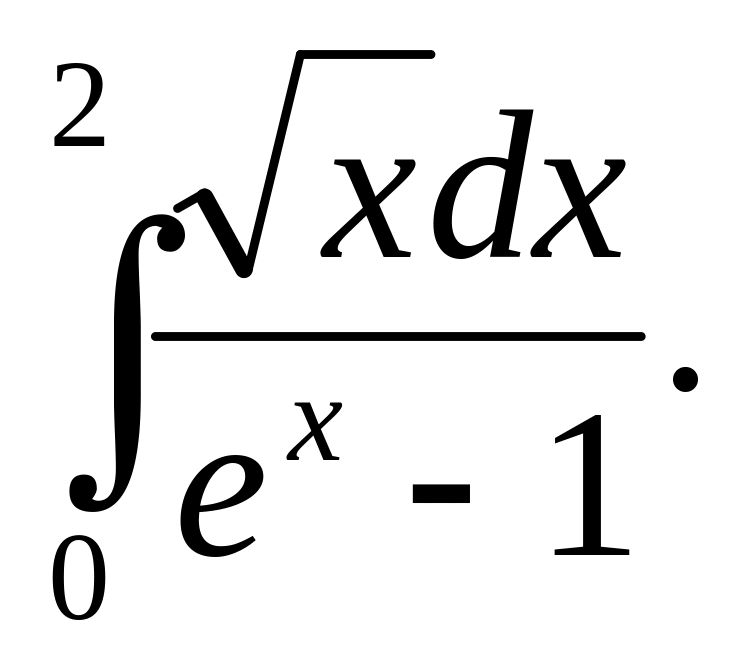
Найти площадь фигуры, ограниченной кривыми

Найти объем тела, ограниченного поверхностями
 и
содержащего часть положительной оси
OZ.
и
содержащего часть положительной оси
OZ.Разложить в ряд Фурье
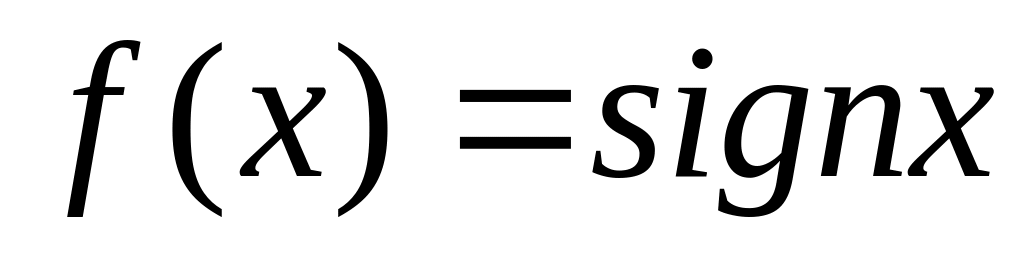 на промежутке
на промежутке

Уровень 2
Найти экстремум функции
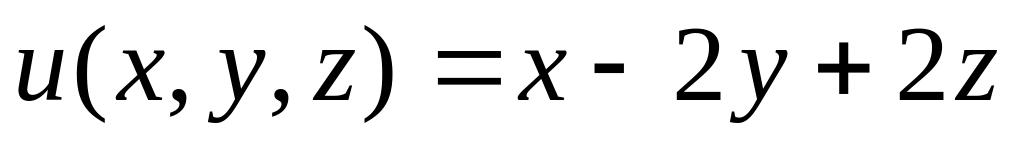 при наличии условия связи
при наличии условия связи
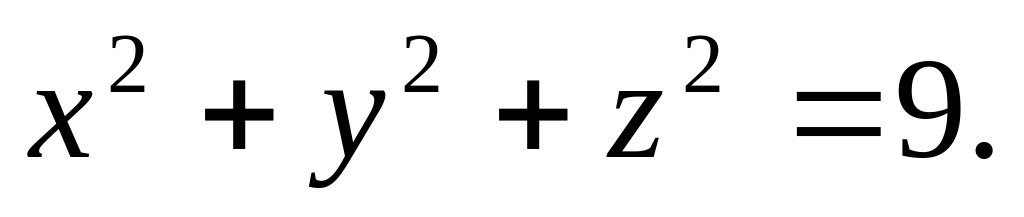 (2006)
(2006)Исследовать на сходимость
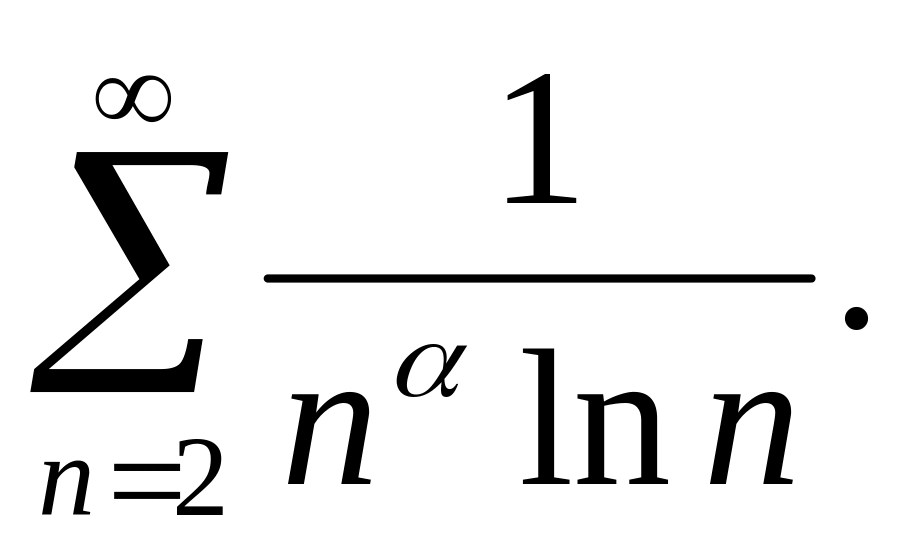 (2007)
(2007)Найти область сходимости интеграла
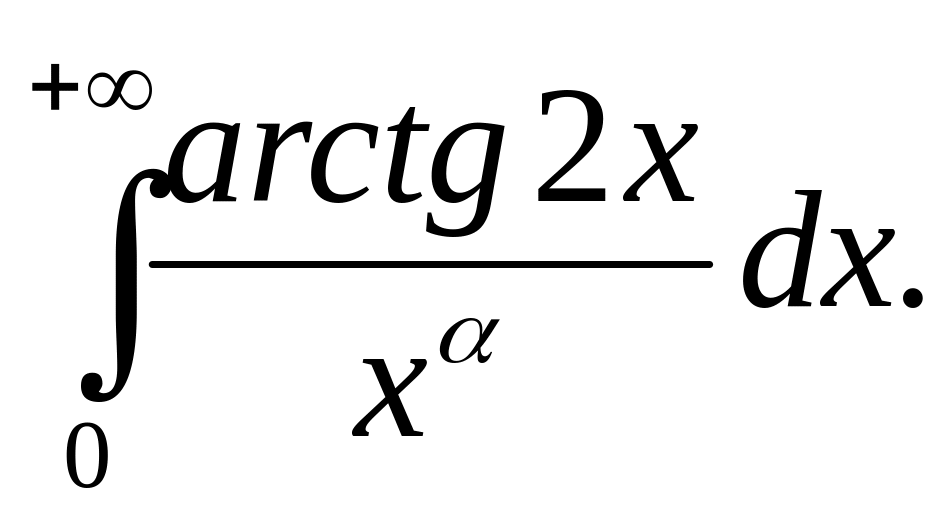 (2007)
(2007)Исследовать функцию
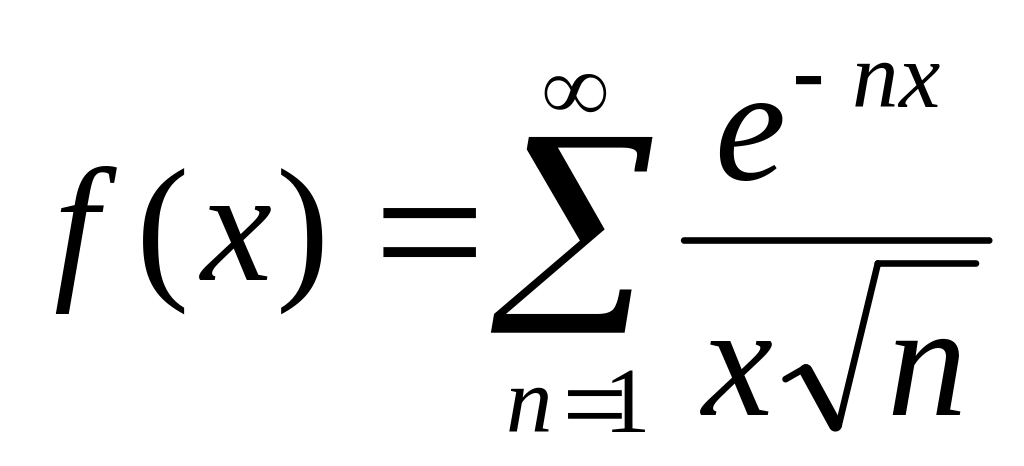 на непрерывность для
на непрерывность для
 (2006)
(2006)Найти площадь фигуры, ограниченной кривой
 (2007)
(2007)Вычислить криволинейный интеграл
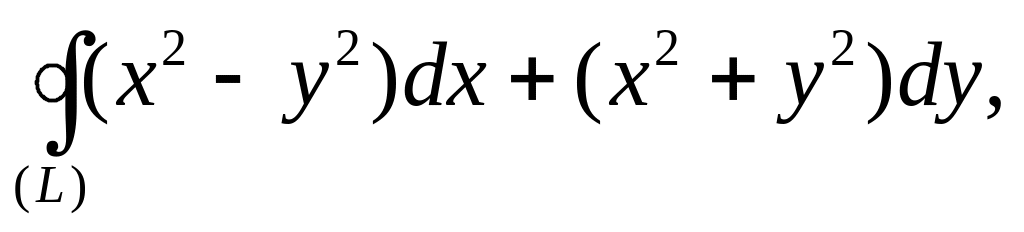 где
где
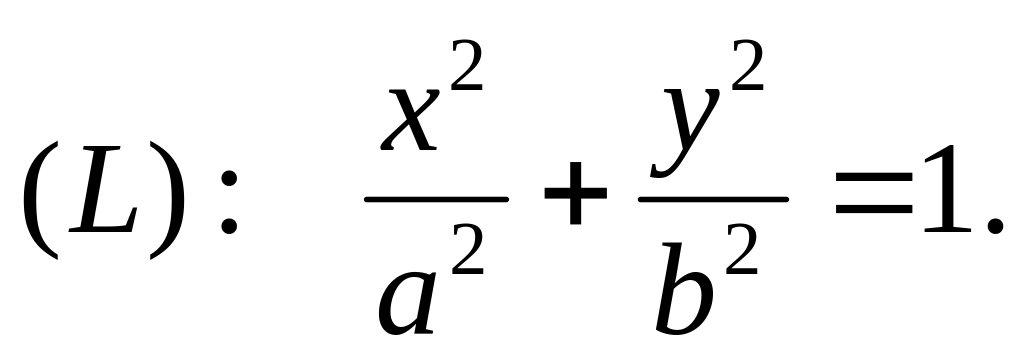
Разложить в ряд Фурье по косинусам
 (2006)
(2006)Разложить в ряд Фурье по синусам
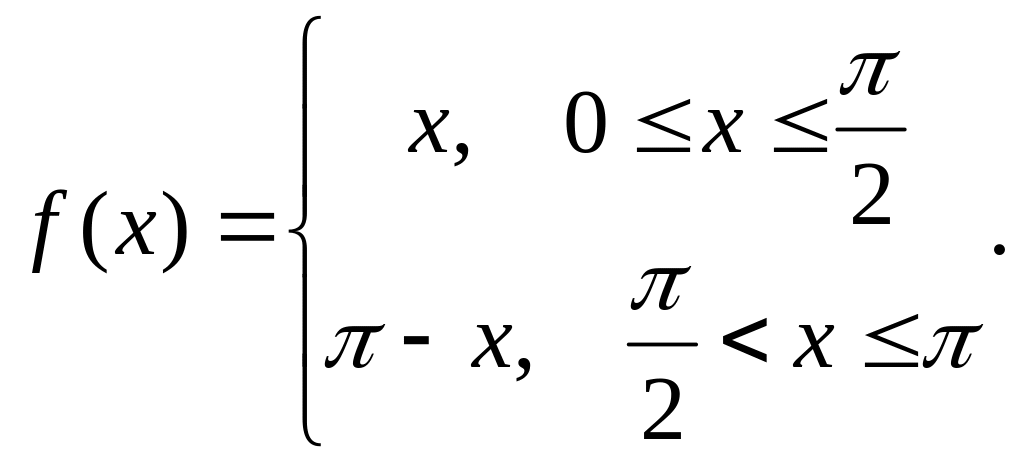
Вычислить интеграл
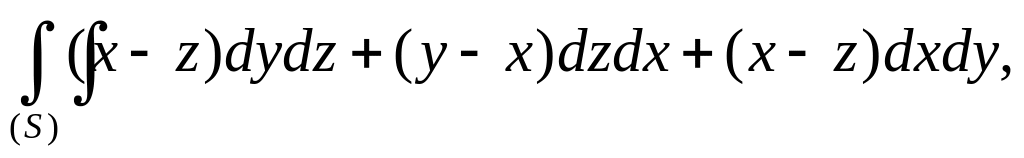 где (S) – внутренняя
сторона поверхности, ограниченная
параболоидом
где (S) – внутренняя
сторона поверхности, ограниченная
параболоидом
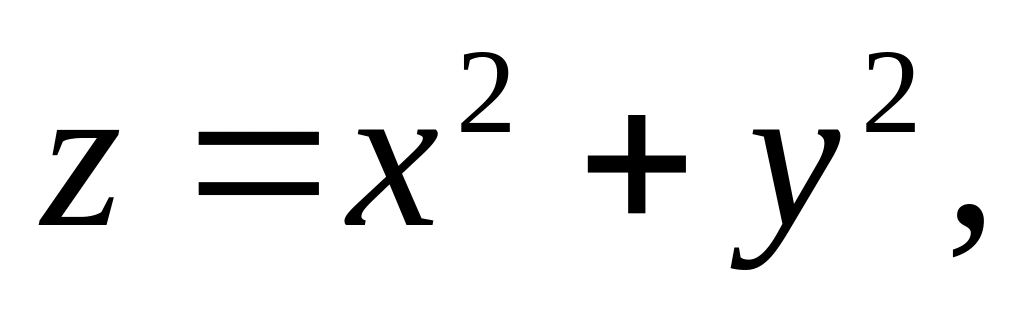 и плоскостью z=4.
и плоскостью z=4.Найти объем тела, ограниченного поверхностями
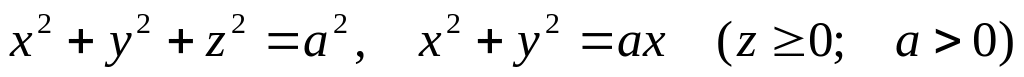 .
.
Вариант 2
Уровень 1
Вычислить
 (2004,
2005)
(2004,
2005)При каком значении a функция f(x) будет непрерывна, если
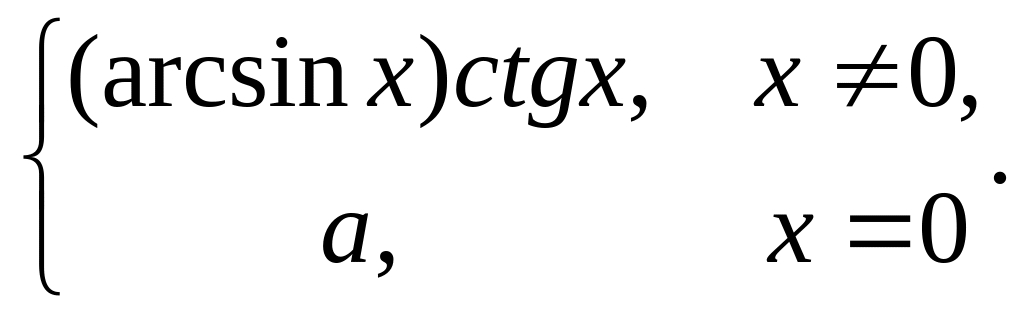 (2004,
2005)
(2004,
2005)Определить значения и , при которых следующая функция всюду дифференцируема:
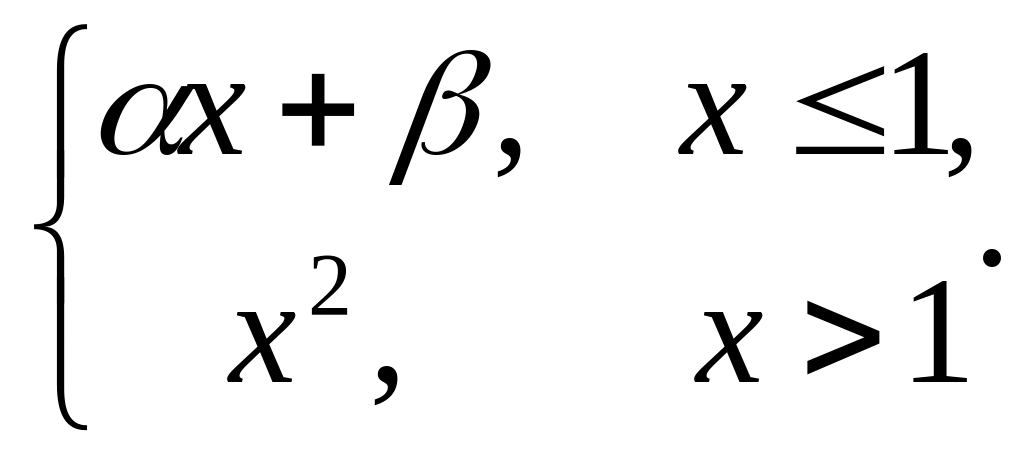 (2004)
(2004)Исследовать на дифференцируемость функцию

Вычислить
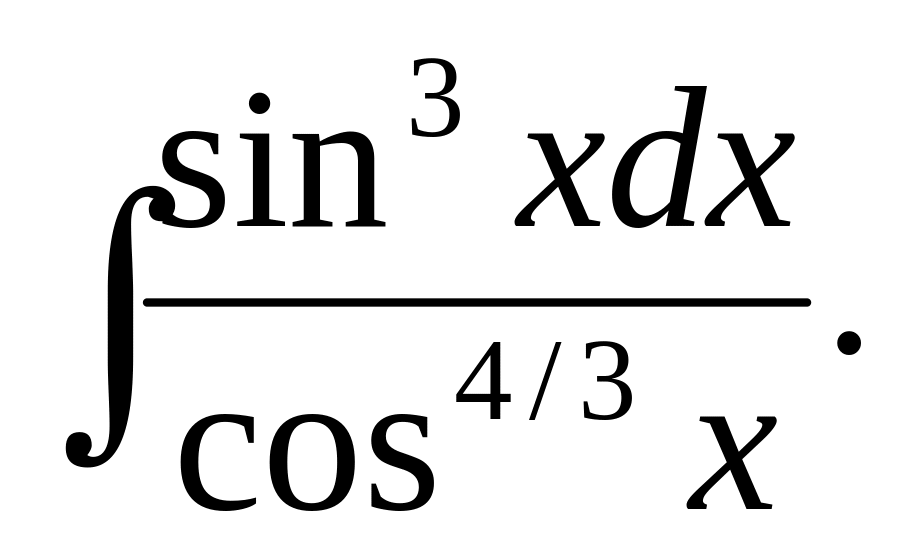 (2004)
(2004)Исследовать на сходимость ряд
 (2004)
(2004)Найти радиус и интервал сходимости ряда
 .
Исследовать ряд в граничных точках
интервала сходимости.
(2004)
.
Исследовать ряд в граничных точках
интервала сходимости.
(2004)Исследовать на сходимость интеграл
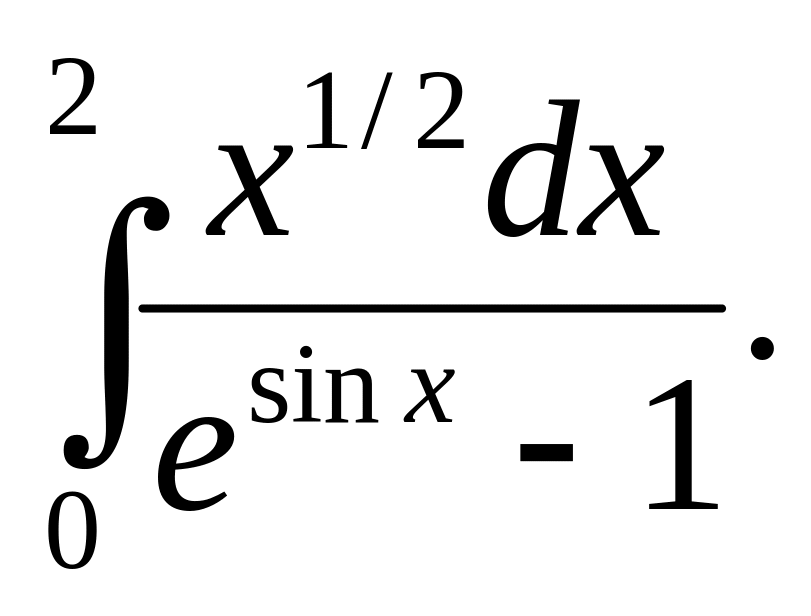 (2004,
2005)
(2004,
2005)Найти площадь фигуры, ограниченной кривыми
 (2004,
2005)
(2004,
2005)Разложить в ряд Фурье функцию
 на отрезке
на отрезке
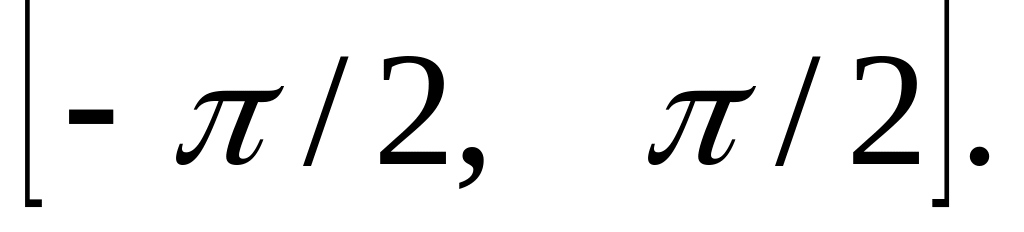 При каких x из промежутка
При каких x из промежутка
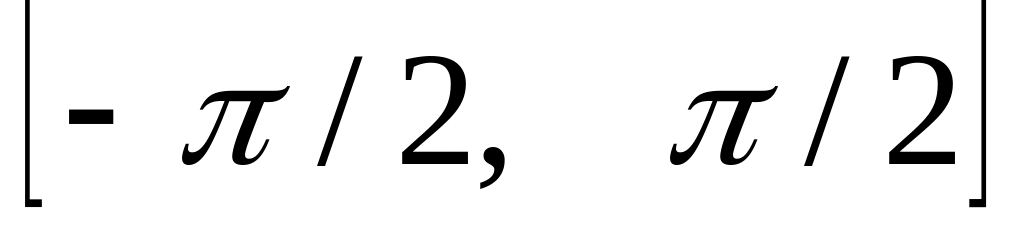 ряд Фурье сходится к
ряд Фурье сходится к
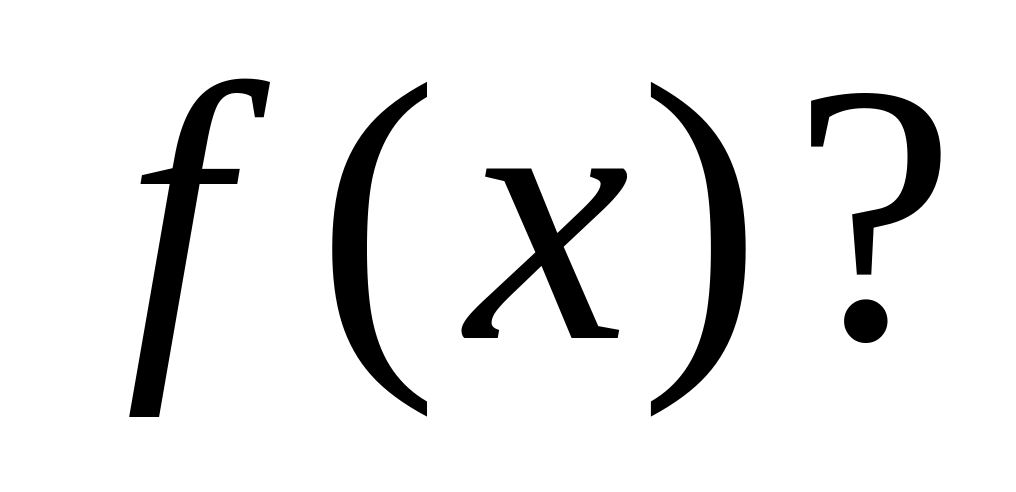
Уровень 2
Вычислить интеграл
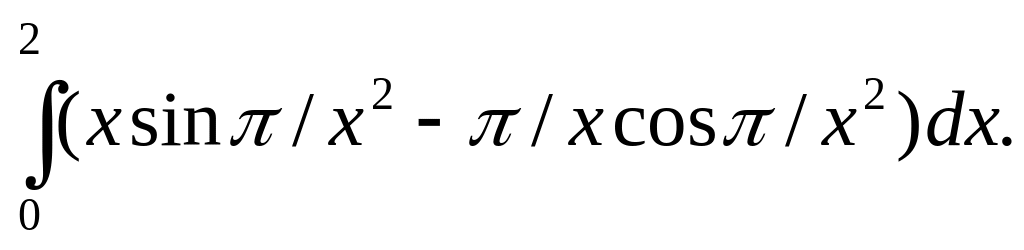
Исследовать на абсолютную и условную сходимость при всех значениях параметра
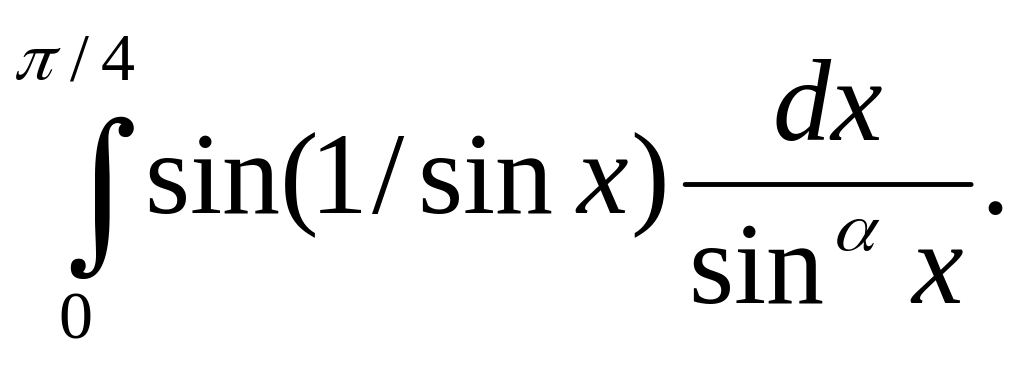
Исследовать на сходимость и абсолютную сходимость ряд
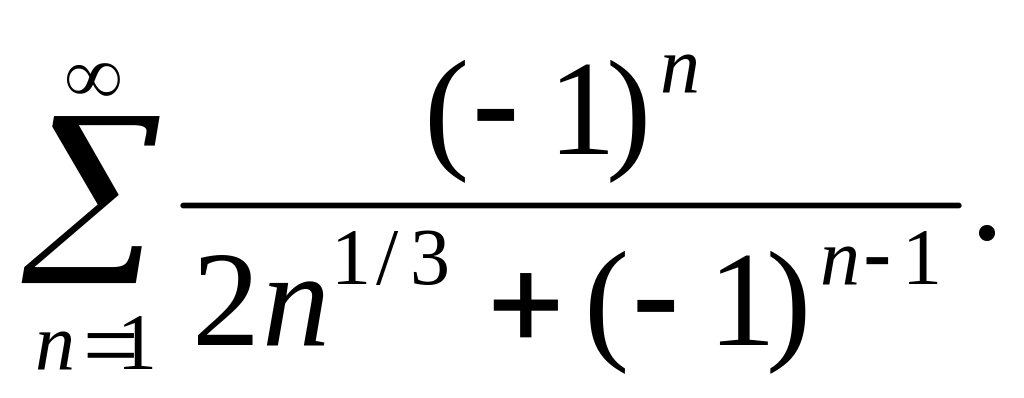
Доказать, что ряд
 сходится равномерно на всей действительной
оси, а ряд
сходится равномерно на всей действительной
оси, а ряд
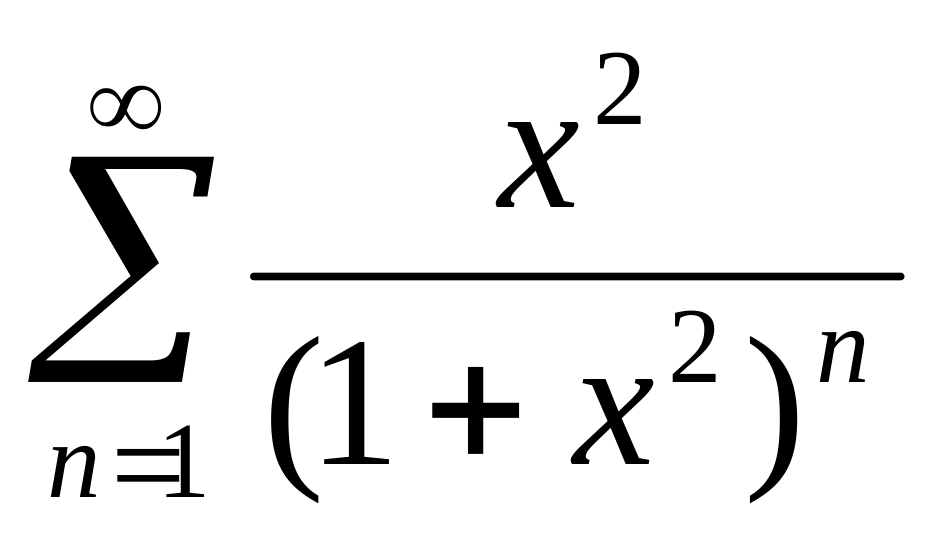 сходится неравномерно.
сходится неравномерно.Найти ряд Фурье в комплексной форме функции
 .
.Доказать, что функция
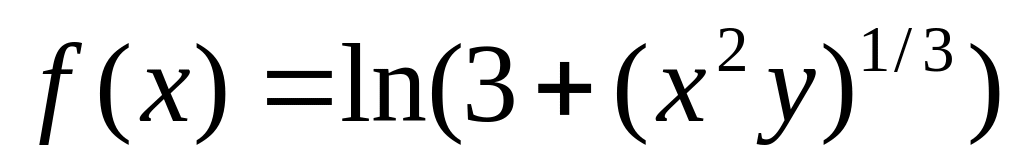 не дифференцируема в точке (0,0).
не дифференцируема в точке (0,0).Найти наибольшее и наименьшее значение функции
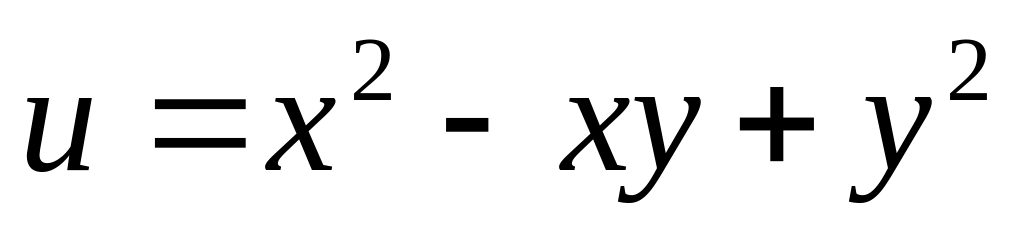 на множестве
на множестве
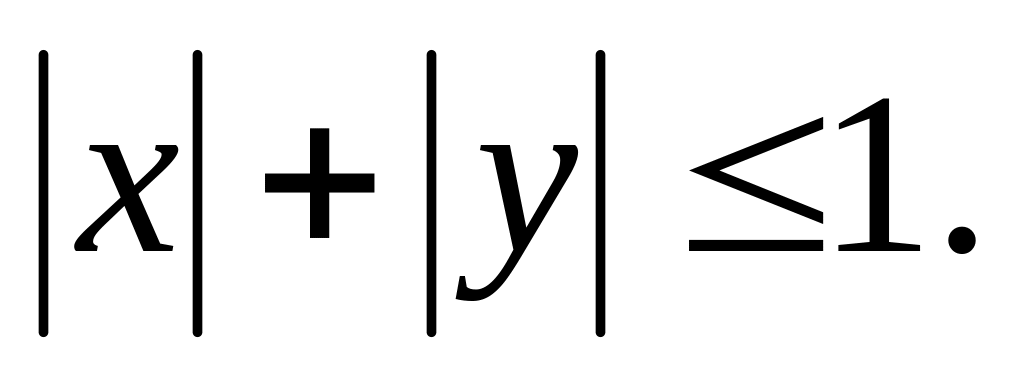
Вычислить двойной интеграл
 где
где

Вычислить интеграл
 где L – кривая
пересечения параболоида
где L – кривая
пересечения параболоида
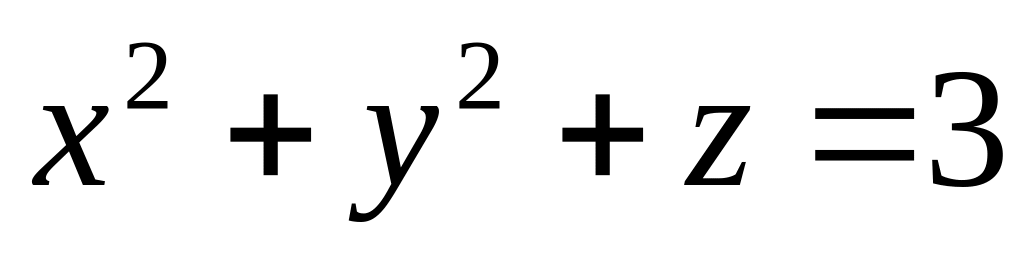 с плоскостью
с плоскостью
 ориентированная положительно относительно
вектора (1,0,0).
ориентированная положительно относительно
вектора (1,0,0).Вычислить интеграл
 где S – внешняя сторона
полной поверхности конуса
где S – внешняя сторона
полной поверхности конуса

Дифференциальные уравнения
Дифференциальное уравнение первого порядка, разрешенное относительно производной y' = f(x,y). Основные методы интегрирования. Теорема Пикара существования и единственности решения задачи Коши.
Линейное дифференциальное уравнение n-го порядка. Задача Коши. Теорема существования и единственности решения задачи Коши. Линейное однородное дифференциальное уравнение n-го порядка. Теорема существования фундаментальной системы решений, теорема о структуре общего решения, метод нахождения фундаментальной системы решений в случае уравнения с постоянными коэффициентами. Линейное неоднородное дифференциальное уравнение n-го порядка. Метод вариации произвольных постоянных нахождения его частного решения. Метод неопределенных коэффициентов для уравнения с постоянными коэффициентами и квазимногочленом в правой части.
Система линейных дифференциальных уравнений. Способ решения линейной однородной системы с постоянными коэффициентами. Метод вариации произвольных постоянных нахождения частного решения линейной неоднородной системы.
Темы практических заданий
Литература
Вопросы по теории (Алексеев А.А.)
Методы интегрирования дифференциальных уравнений 1-го порядка, разрешенных относительно производной (с разделяющимися переменными, однородное, линейное, уравнение Бернулли, в полных дифференциалах). (2008)
Теорема Пикара существования и единственности решения задачи Коши для уравнения
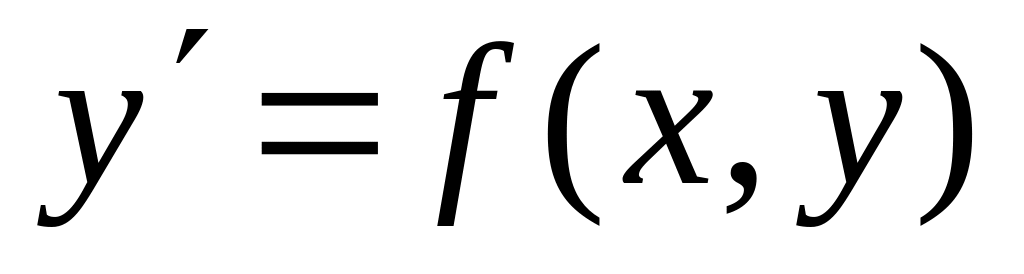 (основные этапы доказательства).
(основные этапы доказательства).Расположение интегральных кривых в окрестности простой особой точки
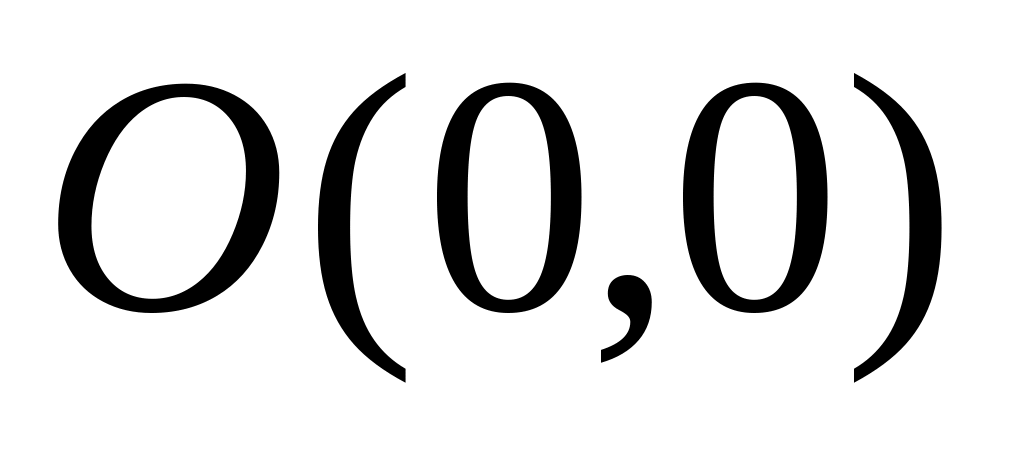 дифференциального уравнения
дифференциального уравнения
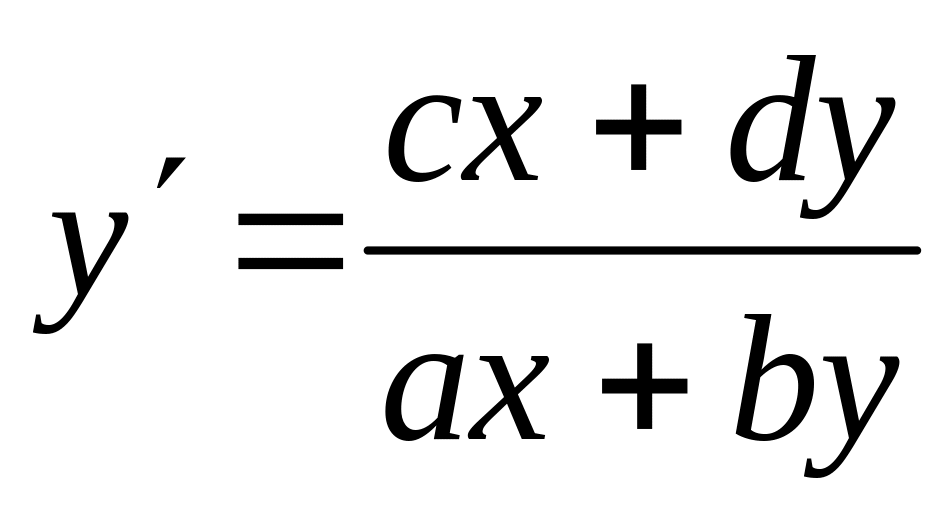 .
.Теорема Коши существования и единственности голоморфного решения дифференциального уравнения .
Однородное линейное дифференциальное уравнение n-го порядка. Фундаментальная система решений. Построение общего решения.
Структура общего решения неоднородного линейного уравнения n-го порядка. Метод вариации произвольных постоянных.
Построение фундаментальной системы решений и общего решения однородного линейного дифференциального уравнения n-го порядка с постоянными коэффициентами. (2008)
Системы дифференциальных уравнений в симметрической форме. Приложение к решению линейных дифференциальных уравнений в частных производных 1-го порядка.
Задачи
Уровень 1
Решить уравнение
 .
Найти интегральную кривую уравнения,
проходящую через точку (1;1).
(2005)
.
Найти интегральную кривую уравнения,
проходящую через точку (1;1).
(2005)Найти решение задачи Коши для уравнения y' = y(1+xy) c начальными данными
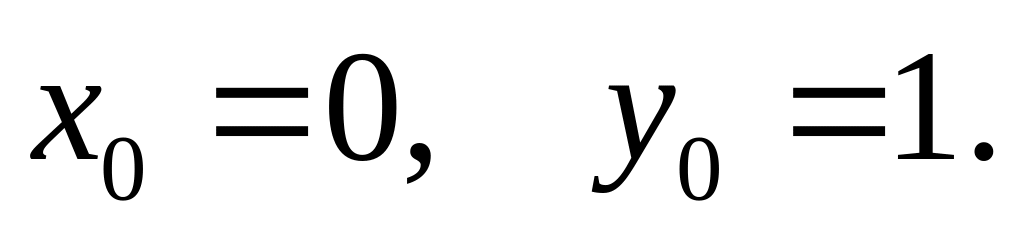 (2005)
(2005)Решить уравнение
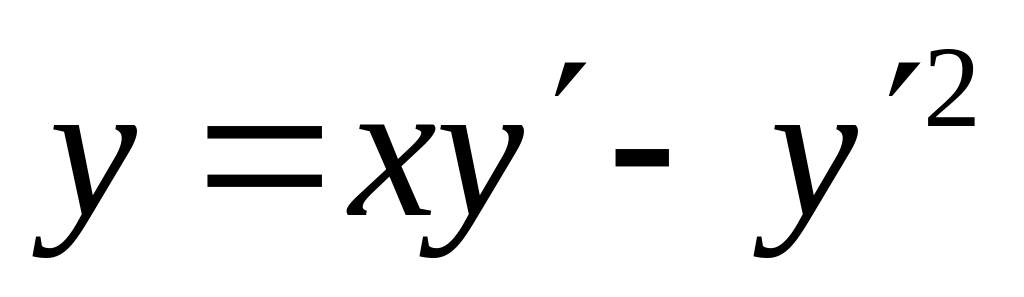 .
Найти также особые решения (если таковые
имеются). (2005)
.
Найти также особые решения (если таковые
имеются). (2005)Найти решение уравнения
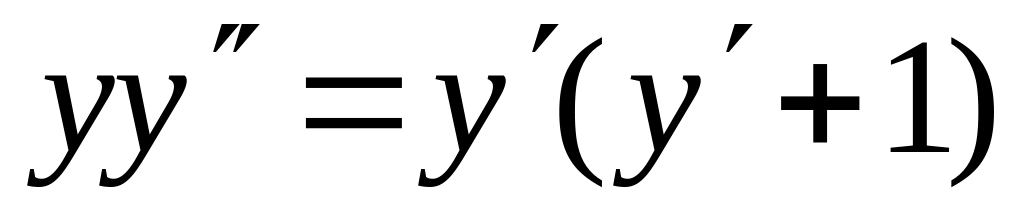 ,
удовлетворяющее начальным условиям
,
удовлетворяющее начальным условиям
 (2005,
2006)
(2005,
2006)Найти решение задачи Коши для уравнения
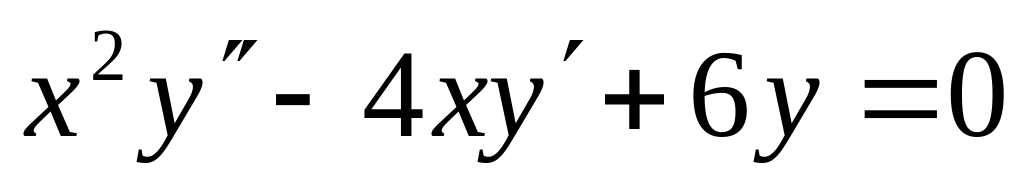 с начальными условиями
с начальными условиями
 (2006)
(2006)Решить уравнение
 (2006)
(2006)Найти решение уравнения
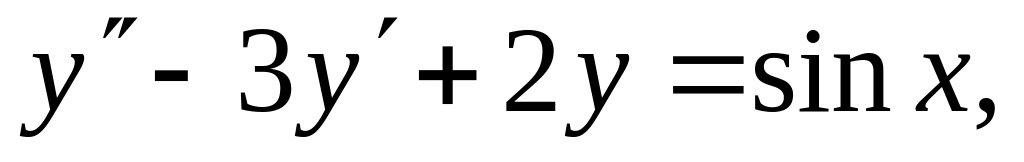 удовлетворяющее начальным условиям
удовлетворяющее начальным условиям
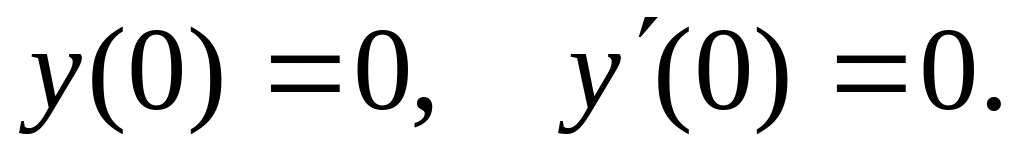 (2007)
(2007)Найти общее решение системы
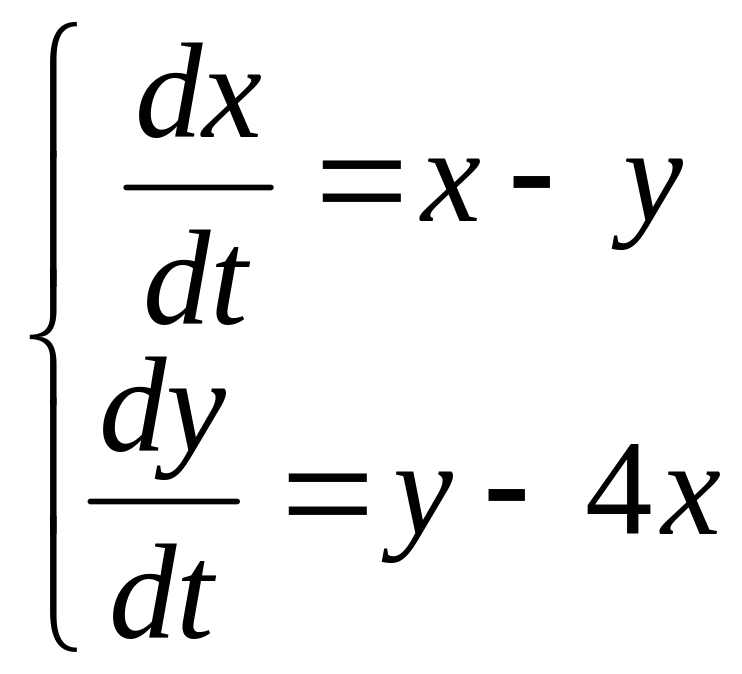 .(2007)
.(2007)Определить тип особой точки
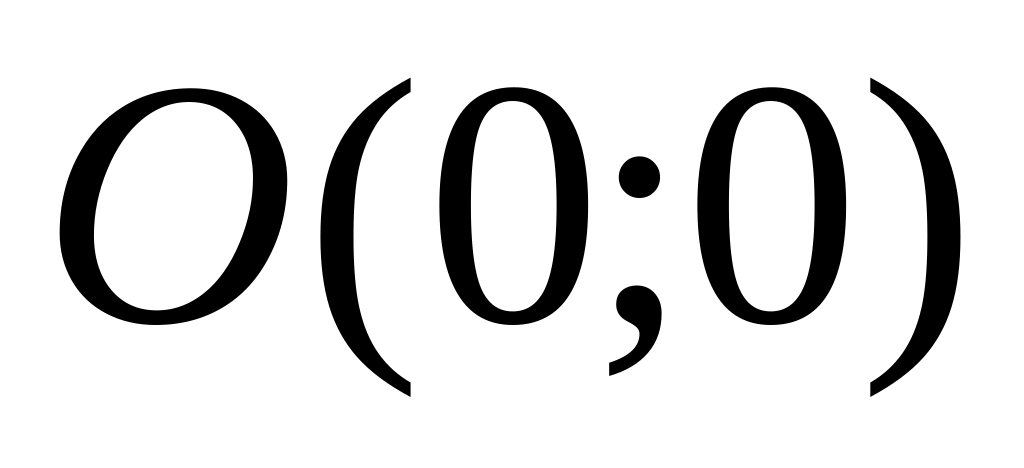 для уравнения
для уравнения
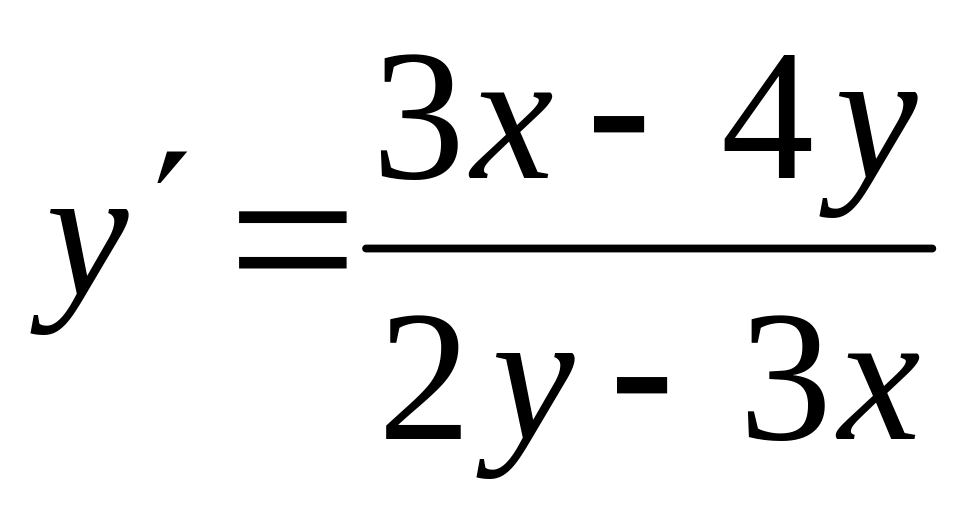 и изобразить его интегральные кривые.
(2007)
и изобразить его интегральные кривые.
(2007)Найти общий интеграл системы
 .
.
Уровень 2
Найти интегральную кривую уравнения
 проходящую через точку (1;0).
проходящую через точку (1;0).Решить уравнение
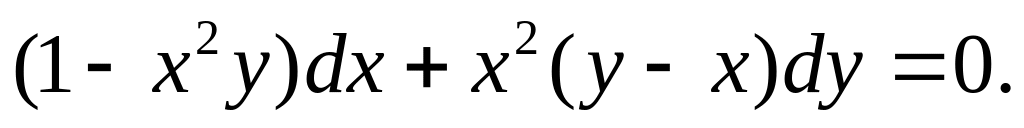
Решить уравнение
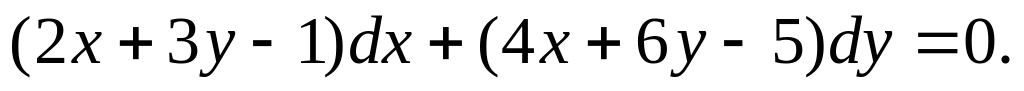
Решить уравнение
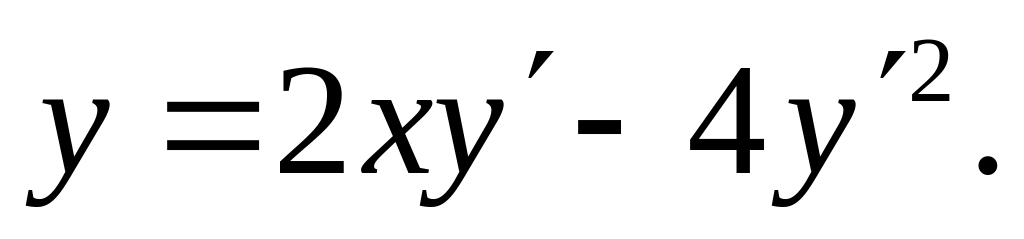 Указать особые решения (если таковые
имеются).
Указать особые решения (если таковые
имеются).Решить уравнение
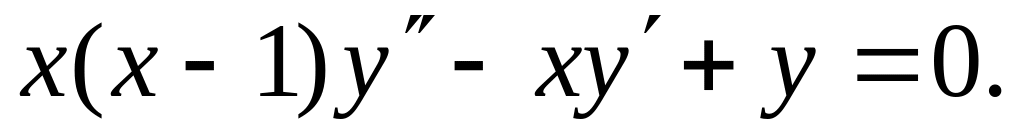
Найти решение уравнения
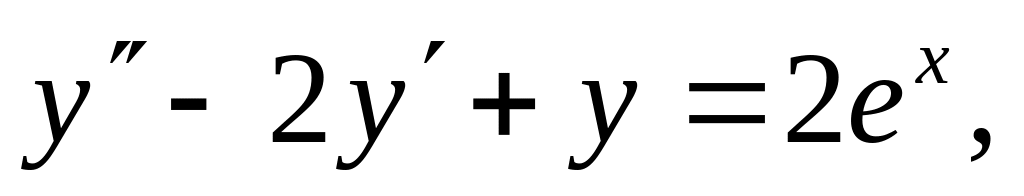 удовлетворяющее начальным условиям
удовлетворяющее начальным условиям
Решить уравнение

Найти общее решение системы
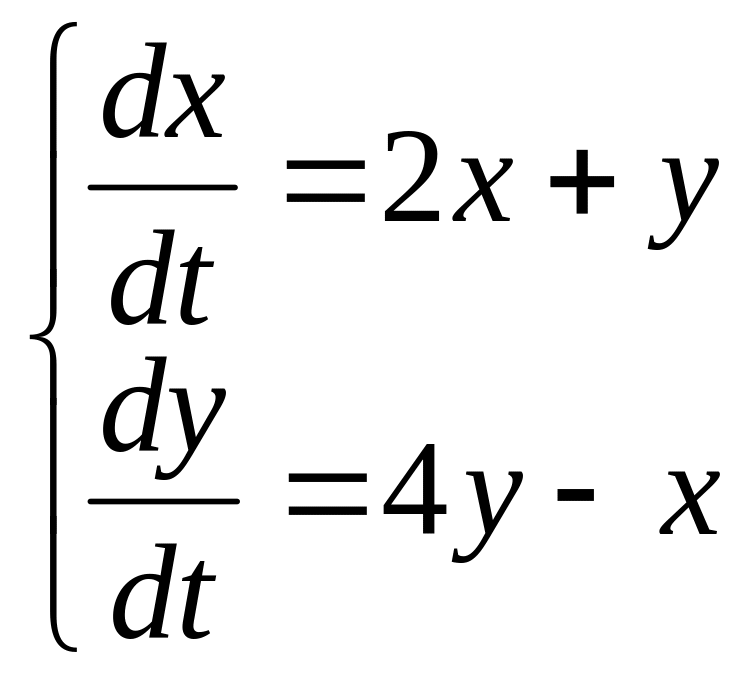 .
.Найти и исследовать все особые точки уравнения
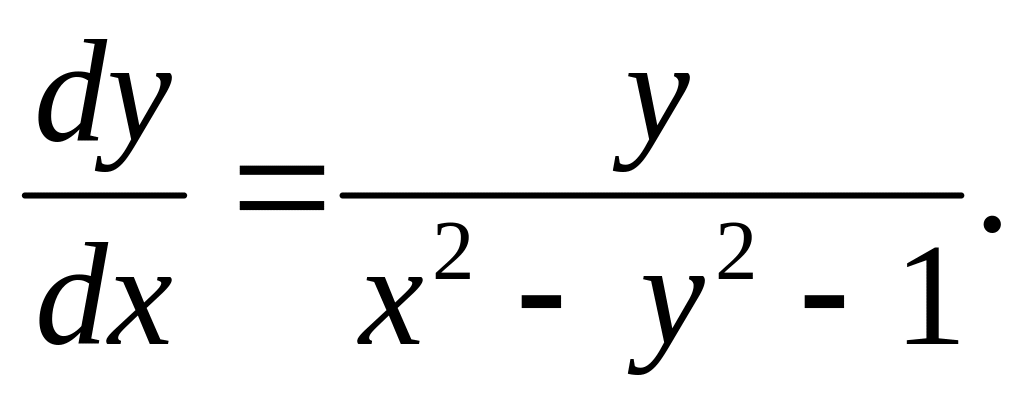
Решить уравнение

